高中数学8.2.1 两角和与差的余弦课后测评

这是一份高中数学8.2.1 两角和与差的余弦课后测评，共7页。试卷主要包含了cs 20°＝，若a＝，b＝，则a·b＝等内容，欢迎下载使用。

A．cs 30°cs 10°－sin 30°sin 10°
B．cs 30°cs 10°＋sin 30°sin 10°
C．sin 30°cs 10°－sin 10°cs 30°
D．cs 30°cs 10°－sin 30°cs 10°
2．若a＝(cs 20°，sin 20°)，b＝(cs 10°，sin 190°)，则a·b＝( )
A． eq \f(1,2) B． eq \f(\r(3),2)
C．cs 10° D． eq \f(\r(2),2)
3．在△ABC中，cs A＝ eq \f(3,5)，cs B＝ eq \f(5,13)，则cs C＝( )
A．－ eq \f(33,65) B． eq \f(33,65)
C．－ eq \f(63,65) D． eq \f(63,65)
4．(多选)已知cs α＝ eq \f(3,5)，cs (α＋β)＝－ eq \f(12,13)，则cs β的值可能为( )
A．－ eq \f(56,65) B．－ eq \f(20,65)
C．－ eq \f(16,65) D． eq \f(15,65)
5．已知sin α＝ eq \f(15,17)，α∈( eq \f(π,2)，π)，则cs ( eq \f(π,3)－α)＝________．
6．已知sin α＝－ eq \f(3,5)，cs β＝ eq \f(5,13)，且α，β均为第四象限角，求下列各式的值：
(1)cs (α＋β)；
(2)cs (α－β).
7．已知cs α＋cs β＝ eq \f(1,2)，sin α＋sin β＝ eq \f(1,3)，则cs (α－β)＝( )
A．－ eq \f(59,72) B． eq \f(59,72) C． eq \f(13,36) D．－ eq \f(13,36)
8．已知点A(cs 80°，sin 80°)，B(cs 20°，sin 20°)，则| eq \(AB,\s\up6(→))|等于( )
A． eq \f(1,2) B． eq \f(\r(2),2) C． eq \f(\r(3),2) D．1
9．若0<α< eq \f(π,2)<β<π，且cs β＝－ eq \f(3,5)，sin (α＋β)＝ eq \f(5,13)，则cs α＝( )
A． eq \f(63,65) B． eq \f(56,65) C． eq \f(16,65) D． eq \f(4,13)
10．已知cs eq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,6)))＝ eq \f(4,5)，cs eq \b\lc\(\rc\)(\a\vs4\al\c1(β－\f(π,6)))＝ eq \f(12,13)，α，β∈ eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,6)))，则cs (α＋β)＝( )
A. eq \f(16,65) B． eq \f(33,65) C． eq \f(56,65) D． eq \f(63,65)
11．(多选)已知α，β，γ∈(0， eq \f(π,2))，sin α＋sin γ＝sin β，cs β＋cs γ＝cs α，则下列说法正确的是( )
A．cs (β－α)＝ eq \f(1,2) B．cs (β－α)＝－ eq \f(1,2)
C．β－α＝ eq \f(π,3) D．β－α＝－ eq \f(π,3)
12．化简下列各式：
(1)cs (θ＋21°)cs (θ－24°)＋sin (θ＋21°)sin (θ－24°)；
(2)cs 15°－sin 15°.
13．已知α∈(0， eq \f(π,2))，tan α＝2，求cs (α－ eq \f(π,4))的值．
14．如图，在平面直角坐标系xOy中，圆O与x轴的正半轴交于点A，点B(－1，2)在圆O上，点C在弧AB上，且∠BOC＝ eq \f(π,4)，求cs ∠AOC的值．
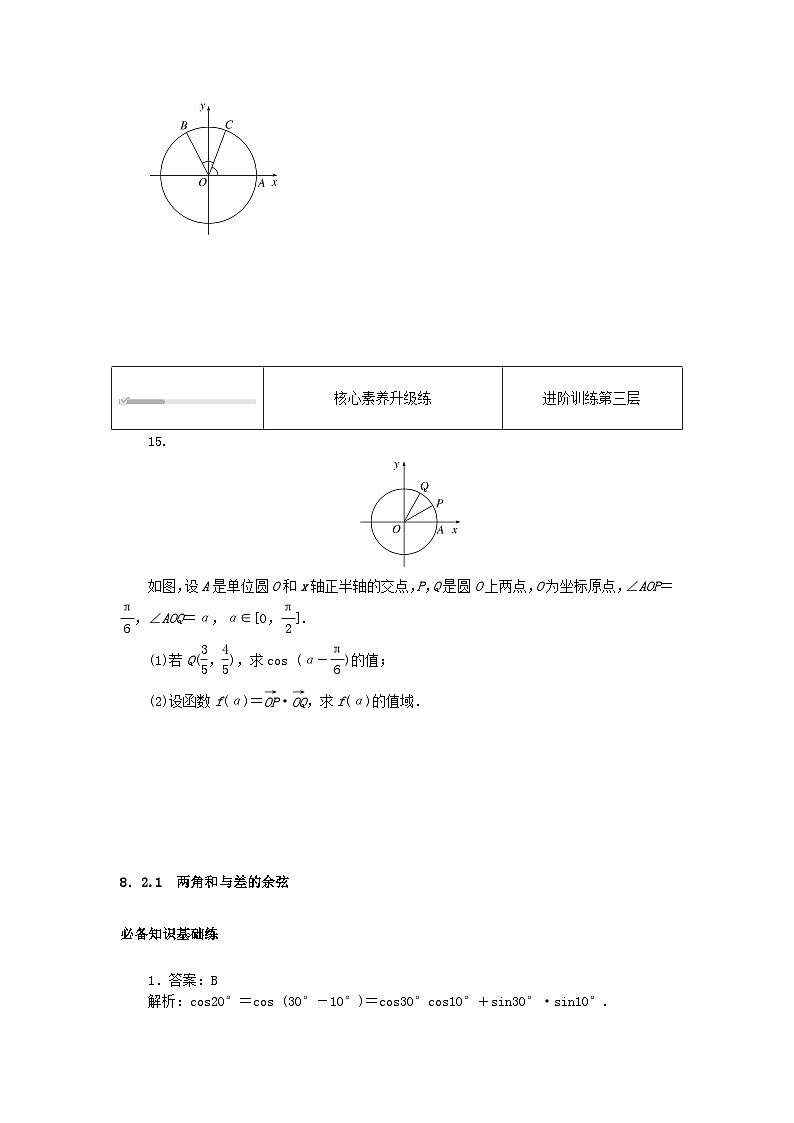
15.
如图，设A是单位圆O和x轴正半轴的交点，P，Q是圆O上两点，O为坐标原点，∠AOP＝ eq \f(π,6)，∠AOQ＝α，α∈[0， eq \f(π,2)].
(1)若Q( eq \f(3,5)， eq \f(4,5))，求cs (α－ eq \f(π,6))的值；
(2)设函数f(α)＝ eq \(OP,\s\up6(→))· eq \(OQ,\s\up6(→))，求f(α)的值域．
8．2.1 两角和与差的余弦
必备知识基础练
1．答案：B
解析：cs20°＝cs (30°－10°)＝cs30°cs10°＋sin30°·sin10°.
2．答案：B
解析：a·b＝cs20°cs10°＋sin20°sin190°＝cs20°cs10°－sin20°sin10°＝cs (20°＋10°)＝cs30°＝eq \f(\r(3),2)，故选B.
3．答案：B
解析：∵csA＝eq \f(3,5)>0，csB＝eq \f(5,13)>0，0∴sinA＝eq \f(4,5)，sinB＝eq \f(12,13)，
∴csC＝－cs (A＋B)＝sinAsinB－csAcsB＝eq \f(4,5)×eq \f(12,13)－eq \f(3,5)×eq \f(5,13)＝eq \f(33,65)，故选B.
4．答案：AC
解析：因csα＝eq \f(3,5)，
则sinα＝±eq \r(1－cs2α)＝±eq \f(4,5)，
又cs(α＋β)＝－eq \f(12,13)，
则sin (α＋β)＝±eq \r(1－cs2（α＋β）)＝±eq \f(5,13)，
cs(α＋β)csα＝－eq \f(12,13)×eq \f(3,5)＝－eq \f(36,65)，
而csβ＝cs [(α＋β)－α]＝cs (α＋β)csα＋sin (α＋β)sinα，
sinα与sin(α＋β)同号，
即sin (α＋β)sinα＝eq \f(20,65)，则csβ＝－eq \f(16,65)，
sinα与sin (α＋β)异号，
即sin (α＋β)sinα＝－eq \f(20,65)，则csβ＝－eq \f(56,65)，
所以csβ的值可能为－eq \f(56,65)或－eq \f(16,65).
故选AC.
5．答案：eq \f(15\r(3)－8,34)
解析：∵sinα＝eq \f(15,17)，α∈(eq \f(π,2)，π)，
∴csα＝－eq \r(1－sin2α)＝－eq \r(1－（\f(15,17)）2)＝－eq \f(8,17).
∴cs(eq \f(π,3)－α)＝cseq \f(π,3)csα＋sineq \f(π,3)sinα＝eq \f(1,2)×(－eq \f(8,17))＋eq \f(\r(3),2)×eq \f(15,17)＝eq \f(15\r(3)－8,34).
6．解析：(1)因为α，β均为第四象限角，
所以csα＝eq \r(1－sin2α)＝eq \f(4,5)，sinβ＝－eq \r(1－cs2β)＝－eq \f(12,13)，
所以cs(α＋β)＝csαcsβ－sinαsinβ＝eq \f(4,5)×eq \f(5,13)－eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3,5)))×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(12,13)))＝eq \f(20,65)－eq \f(36,65)＝－eq \f(16,65).
(2)由(1)知：csα＝eq \f(4,5)，sinβ＝－eq \f(12,13)，
所以cs (α－β)＝csαcsβ＋sinαsinβ＝eq \f(4,5)×eq \f(5,13)＋eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3,5)))×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(12,13)))＝eq \f(20,65)＋eq \f(36,65)＝eq \f(56,65).
关键能力综合练
7．答案：A
解析：(csα＋csβ)2＝cs2α＋2csαcsβ＋cs2β＝eq \f(1,4)，
(sinα＋sinβ)2＝sin2α＋2sinαsinβ＋sin2β＝eq \f(1,9)，
两式相加，得2＋2cs(α－β)＝eq \f(13,36)，
则cs (α－β)＝－eq \f(59,72)，故选A.
8．答案：D
解析：||＝eq \r(（cs80°－cs20°）2＋（sin80°－sin20°）2)
＝eq \r(2－2（cs80°cs20°＋sin80°sin20°）)
＝eq \r(2－2cs60°)＝eq \r(2－2×\f(1,2))＝1.
9．答案：B
解析：∵csβ＝－eq \f(3,5)，eq \f(π,2)<β<π，∴sinβ＝eq \f(4,5)，
∵0<α∴eq \f(π,2)<α＋β∴cs (α＋β)＝－eq \r(1－\f(25,169))＝－eq \f(12,13)，
∴csα＝cs [(α＋β)－β]＝cs (α＋β)csβ＋sin (α＋β)sinβ＝－eq \f(12,13)×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3,5)))＋eq \f(5,13)×eq \f(4,5)＝eq \f(56,65).
故选B.
10．答案：D
解析：∵cseq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,6)))＝eq \f(4,5)，cseq \b\lc\(\rc\)(\a\vs4\al\c1(β－\f(π,6)))＝eq \f(12,13)，α，β∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,6)))，
∴α＋eq \f(π,6)∈(eq \f(π,6)，eq \f(π,3))，β－eq \f(π,6)∈(－eq \f(π,6)，0)，
∴sineq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,6)))>0，sineq \b\lc\(\rc\)(\a\vs4\al\c1(β－\f(π,6)))<0，
∴sineq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,6)))＝eq \r(1－cs2\b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,6))))＝eq \f(3,5)，
sineq \b\lc\(\rc\)(\a\vs4\al\c1(β－\f(π,6)))＝－eq \r(1－cs2\b\lc\(\rc\)(\a\vs4\al\c1(β－\f(π,6))))＝－eq \f(5,13)，
∴cs(α＋β)＝cseq \b\lc\[\rc\](\a\vs4\al\c1(\b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,6)))＋\b\lc\(\rc\)(\a\vs4\al\c1(β－\f(π,6)))))
＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(β－\f(π,6)))cseq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,6)))－sineq \b\lc\(\rc\)(\a\vs4\al\c1(β－\f(π,6)))sineq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,6)))
＝eq \f(4,5)×eq \f(12,13)－eq \f(3,5)×(－eq \f(5,13))＝eq \f(63,65).
故选D.
11．答案：AC
解析：由已知，得sinγ＝sinβ－sinα，csγ＝csα－csβ.
两式分别平方相加，得(sinβ－sinα)2＋(csα－csβ)2＝1.
∴－2cs (β－α)＝－1，∴cs (β－α)＝eq \f(1,2)，
∴A正确，B错误．
∵sinγ＝sinβ－sinα>0，∴β>α，∴β－α＝eq \f(π,3)，
∴C正确，D错误，故选AC.
12．解析：(1)原式＝cs [(θ＋21°)－(θ－24°)]＝cs45°＝eq \f(\r(2),2).
(2)原式＝eq \r(2)(eq \f(\r(2),2)cs15°－eq \f(\r(2),2)sin15°)
＝eq \r(2)(cs45°cs15°－sin45°sin15°)＝eq \r(2)cs (45°＋15°)
＝eq \r(2)cs60°＝eq \f(\r(2),2).
13．解析：因为tanα＝eq \f(sinα,csα)＝2，
所以sinα＝2csα，又sin2α＋cs2α＝1，
结合α∈(0，eq \f(π,2))，所以sinα＝eq \f(2\r(5),5)，csα＝eq \f(\r(5),5)，
则cs (α－eq \f(π,4))＝csαcseq \f(π,4)＋sinαsineq \f(π,4)＝eq \f(\r(5),5)×eq \f(\r(2),2)＋eq \f(2\r(5),5)×eq \f(\r(2),2)＝eq \f(3\r(10),10).
14．解析：因为点B(－1，2)在∠AOB的终边上，
所以sin∠AOB＝eq \f(2,\r(1＋4))＝eq \f(2,\r(5))，cs∠AOB＝eq \f(－1,\r(1＋4))＝－eq \f(1,\r(5))，
因为∠AOC＝∠AOB－∠BOC，∠BOC＝eq \f(π,4)，
所以∠AOC＝∠AOB－eq \f(π,4)，
所以cs∠AOC＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(∠AOB－\f(π,4)))
＝cs∠AOBcseq \f(π,4)＋sin∠AOBsineq \f(π,4)
＝－eq \f(1,\r(5))×eq \f(\r(2),2)＋eq \f(2,\r(5))×eq \f(\r(2),2)＝eq \f(\r(10),10).
核心素养升级练
15．解析：(1)因为Q(eq \f(3,5)，eq \f(4,5))，∠AOQ＝α，α∈[0，eq \f(π,2)]，
所以sinα＝eq \f(4,5)，csα＝eq \f(3,5)，
则cs (α－eq \f(π,6))＝csα·eq \f(\r(3),2)＋sinα·eq \f(1,2)＝eq \f(4＋3\r(3),10).
(2)由题意得Q(csα，sinα)，因为∠AOP＝eq \f(π,6)，
则P(eq \f(\r(3),2)，eq \f(1,2))，
所以·＝eq \f(\r(3),2)csα＋eq \f(1,2)sinα，
即函数f(α)＝eq \f(\r(3),2)csα＋eq \f(1,2)sinα＝cs (α－eq \f(π,6)).
由α∈[0，eq \f(π,2)]，得α－eq \f(π,6)∈[－eq \f(π,6)，eq \f(π,3)]，
所以f(α)∈[eq \f(1,2)，1].
必备知识基础练
进阶训练第一层
关键能力综合练
进阶训练第二层
核心素养升级练
进阶训练第三层