

2023-2024学年山东省淄博市临淄区六年级(上)期中数学试卷(五四学制)
展开1、考生须诚信考试,遵守考场规则和考试纪律,并自觉服从监考教师和其他考试工作人员
管理;
2、监考教师发卷后,在试卷指定的地方填写本人准考证号、姓名等信息;考试中途考生不准以任何理由离开考场;
3、考生答卷用笔必须使用同一规格同一颜色的笔作答(作图可使用铅笔) ,不准用规定以外的笔答卷,不准在答卷上作任何标记。考生书写在答题卡规定区域外的答案无效。
4、考试开始信号发出后,考生方可开始作答。
一、选择题(共10小题,每小题4分,满分40分)
1.(4分)下列图形旋转一周,能得到如图几何体的是( )
A.B.C.D.
2.(4分)一种面粉的质量标识为“25±0.25千克”,则下列面粉中合格的是( )
A.24.70千克B.25.30千克C.24.80千克D.25.51千克
3.(4分)临淄区太公湖水利风景区,坐落于牛山脚下,南依风景旅游区马莲台,该湖上下游长2500米,宽300﹣500米3,其中1500000用科学记数法表示为( )
A.1.5×105B.1.5×106C.15×106D.0.15×106
4.(4分)下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A.B.
C.D.
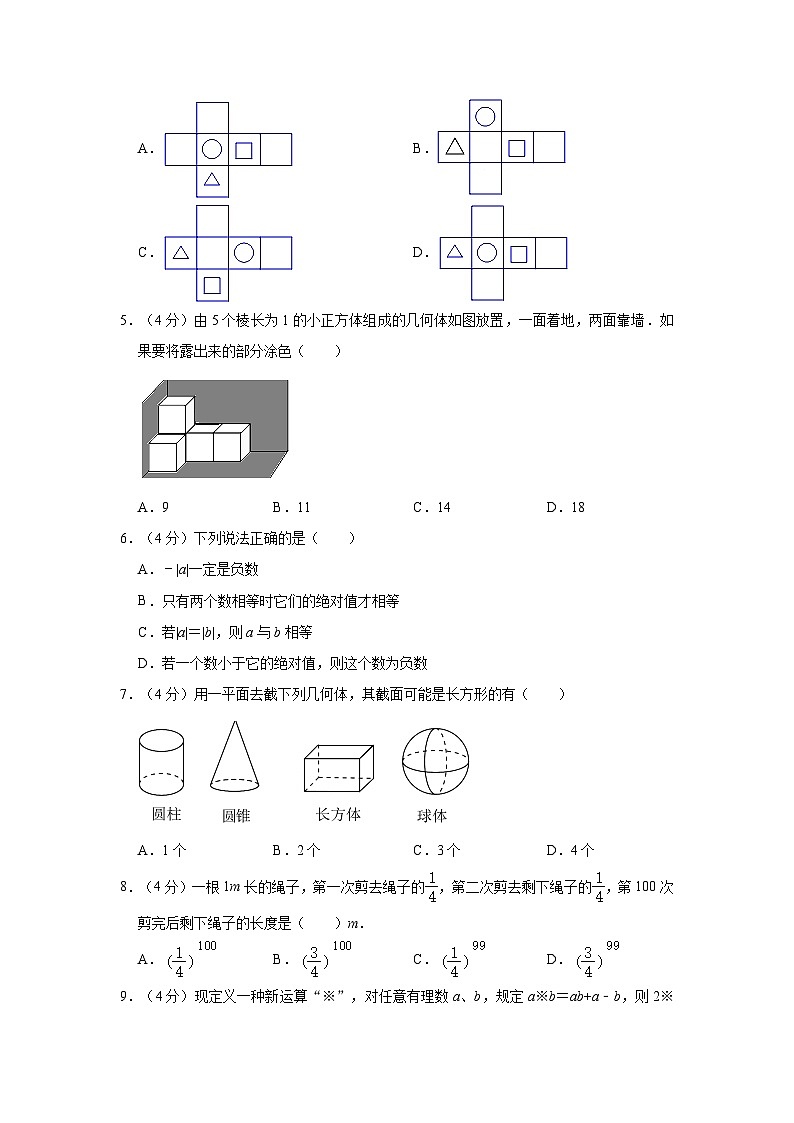
5.(4分)由5个棱长为1的小正方体组成的几何体如图放置,一面着地,两面靠墙.如果要将露出来的部分涂色( )
A.9B.11C.14D.18
6.(4分)下列说法正确的是( )
A.﹣|a|一定是负数
B.只有两个数相等时它们的绝对值才相等
C.若|a|=|b|,则a与b相等
D.若一个数小于它的绝对值,则这个数为负数
7.(4分)用一平面去截下列几何体,其截面可能是长方形的有( )
A.1个B.2个C.3个D.4个
8.(4分)一根1m长的绳子,第一次剪去绳子的,第二次剪去剩下绳子的,第100次剪完后剩下绳子的长度是( )m.
A.B.C.D.
9.(4分)现定义一种新运算“※”,对任意有理数a、b,规定a※b=ab+a﹣b,则2※(﹣3)等于( )
A.﹣3B.﹣2C.﹣1D.0
10.(4分)已知|x|=5,|y|=2,且|x+y|=﹣x﹣y( )
A.±3B.±3或±7C.﹣3或7D.﹣3或﹣7
二、填空题(每小题4分,共20分)
11.(4分)比较大小:﹣2 ﹣2.3.(填“>”、“<”或“=”)
12.(4分)把近似数32.6759精确到百分位的结果是 .
13.(4分)使用科学计算器进行计算,其按键顺序为:
则输出结果为 .
14.(4分)若x,y为有理数,且|x+2|+(y﹣2)2=0,则的值为 .
15.(4分)一跳蚤在一直线上从O点开始,第1次向右跳1个单位长度,紧接着第2次向左跳2个单位长度,第4次向左跳4个单位长度……依此规律跳下去,当它跳第99次落下时 个单位长度.
三、解答题(第16,17,18,19题每题10分;第20,21题每题12分,第22,23题每题13分;满分90分)解答要写出必要的文字说明、证明过程或演算步骤.
16.计算:
(1)﹣;
(2)﹣2÷4×.
17.请在数轴上表示各数﹣4,|﹣2.5|,﹣|3|,,﹣(﹣1),0
18.妈妈给圆柱形的玻璃杯(底面直径16cm,高20cm)做了一个布套(包住侧面)
(1)求出至少用布料多少平方厘米?
(2)求这个杯子最多可以盛水多少立方厘米?
19.如图,是由几个大小相同的小正方体所搭成的几何体从上面看到的形状图,小正方形中的数字表示在这个位置小正方体的个数.
(1)请画出从正面、左面看到的这个几何体的形状图;
(2)若每个小正方体棱长为1cm,请直接写出该几何体的表面积(包含底面)为 .
20.(12分)计算:
(1);
(2)﹣12×(﹣5)÷[(﹣3)2+2×(﹣5)].
21.(12分)结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示﹣3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.
(2)如果|x+1|=3,求数x;
(3)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值.
22.(13分)(1)已知a、b互为相反数,c、d互为倒数,m的绝对值等于32+的值为 .
(2)如果a,b表示有理数,且ab<0,求
23.(13分)某水果店以每箱200元的价格从水果批发市场购进20箱樱桃,若以每箱净重10千克为标准,超过的千克数记为正数,称重的记录如下表:
(1)求n的值及这20箱樱桃的总重量;
(2)若水果店打算以每千克25元销售这批樱桃,若全部售出可获利多少元;
(3)实际上该水果店第一天以(2)中的价格只销售了这批樱桃的60%,第二天因为害怕剩余樱桃腐烂,水果店在销售这批樱桃过程中是盈利还是亏损,盈利或亏损多少元.
2023-2024学年山东省淄博市临淄区六年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(本题共10小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项填在下面的表中.每小题4分,满分40分,错选、不选或选出的答案超过一个,均记0分.)
1.【分析】根据每一个几何体的特征判断即可.
解:A、将图形绕直线旋转一周,故A符合题意;
B、将图形绕直线旋转一周,故B不符合题意;
C、将图形绕直线旋转一周,故C不符合题意;
D、将图形绕直线旋转一周,故D不符合题意;
故选:A.
【点评】本题考查了点、线、面、体,熟练掌握每一个几何体的特征是解题的关键.
2.【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
解:“25±0.25千克”表示合格范围在25上下0.25的范围内的是合格品,即24.75到25.25之间的合格,
因为24.75<24.80<25.25,
故只有24.80千克合格.
故选:C.
【点评】此题考查正负数在实际生活中的应用,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.
3.【分析】直接根据科学记数法的定义作答即可.
解:1500000=1.5×107,
故选:B.
【点评】本题主要考查了用科学记数法表示较大的数,科学记数法的表现形式为a×10n的形式,其中1≤|a|<10,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,当原数绝对值大于等于10时,n是正数,当原数绝对值小于1时n是负数.
4.【分析】根据展开图邻面间的关系,可得答案.
解:由正方体图,得
三角形面、正方形面,故A符合题意,
故选:A.
【点评】本题考查了展开图折叠成几何体,利用正方体邻面间的关系是解题关键.
5.【分析】由涂色部分面积是从上、前、右三个方向所涂面积相加,据此可得.
解:由图可知涂色部分是从上、前、右三个方向所涂面积相加,
故选:B.
【点评】本题主要考查几何体的表面积,解题的关键是掌握涂色部分是从上、前、右三个方向所涂面积相加的结果.
6.【分析】根据相反数和绝对值的性质,对选项进行一一分析,排除错误答案.
解:A、﹣|a|不一定是负数,结果还是0;
B、互为相反数的两个数的绝对值也相等;
C、a,b互为相反数或等于0时,故错误;
D、若一个数小于它的绝对值,符合绝对值的性质.
故选:D.
【点评】本题考查了绝对值的性质.一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
7.【分析】根据圆柱、圆锥、长方体、球的形状判断即可.
解:圆锥和圆台不可能得到长方形截面,
圆柱和长方体能得到长方形截面,
球的截面是圆;
截面可能是长方形的有2个.
故选:B.
【点评】本题考查图形的认识及截面图形分类,仔细观察是解决问题的关键.
8.【分析】根据有理数的乘方运算法则即可求出答案.
解:第一次剪去绳子的,剩下是m,
第二次剪去剩下绳子的,剩下是=m,
第三次剪去剩下绳子的,剩下是=m,
……,
第100次剪完后剩下绳子的长度是m,
故选:B.
【点评】本题考查有理数的乘方,解题的关键是正确找出题中的规律.
9.【分析】原式利用已知的新定义计算即可得到结果.
解:根据题中的新定义得:2※(﹣3)=﹣6+2+3=﹣6,
故选:C.
【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
10.【分析】根据|x|=5,|y|=2,求出x=±5,y=±2,然后根据|x+y|=﹣x﹣y,可得x+y≤0,然后分情况求出x﹣y的值.
解:∵|x|=5,|y|=2,
∴x=±2、y=±2,
又|x+y|=﹣x﹣y,
∴x+y<0,
则x=﹣5、y=2或x=﹣5,
所以x﹣y=﹣5或﹣3,
故选:D.
【点评】本题考查了绝对值以及有理数的加减法,解答本题的关键是根据题目所给的条件求出x和y的值.
二、填空题(每小题4分,共20分)
11.【分析】直接根据负数比较大小的法则进行比较即可.
解:∵|﹣2|=2,|﹣2.3|=3.3,
∴﹣2.33<﹣3.3,
∴﹣2<﹣2.4.
故答案为:<.
【点评】本题考查的是有理数的大小比较,熟知负数比较大小的法则是解答此题的关键.
12.【分析】根据四舍五入法可以解答本题.
解:32.6759≈32.68.
故答案为:32.68.
【点评】本题考查近似数和有效数字,解答本题的关键是明确近似数和有效数字的含义.
13.【分析】根据科学计算器得出结论即可.
解:使用科学计算器进行计算3×(﹣2)3×,结果为:﹣32,
故答案为:﹣32.
【点评】本题主要考查科学计算器的使用,熟练掌握科学计算器的使用是解题的关键.
14.【分析】先根据非负数的性质求出x、y的值,然后代值计算即可.
解:∵|x+2|+(y﹣2)2=0,|x+2|≥42≥0,
∴x+5=0,y﹣2=8,
∴x=﹣2,y=2,
∴,
故答案为:﹣1.
【点评】本题主要考查了非负数的性质,代数式求值,正确根据非负数的性质求出x、y的值是解题的关键.
15.【分析】根据题意,可以写出前几次落点可以用哪些数字表示,从而可以发现数字的变化特点,从而可以得到当它跳第99次落下时,落点处离点O的距离是多少个单位长度即可.
解:设向右为正,向左为负,
1+(﹣2)+8+(﹣4)+⋯+99
=[1+(﹣4)]+[3+(﹣4)]+⋯+[97+(﹣98)]+99
=﹣49+99
=50,
故当它跳第99次落下时,落点处在点O的距离是50个单位长度,
故答案为:50.
【点评】本题考查有理数加法的应用,落点处离点O的距离是多少个单位长度,是解决问题的关键.
三、解答题(第16,17,18,19题每题10分;第20,21题每题12分,第22,23题每题13分;满分90分)解答要写出必要的文字说明、证明过程或演算步骤.
16.【分析】(1)根据有理数的减法进行计算即可求解.
(2)根据有理数的乘除混合运算进行计算即可求解.
解:(1)
=
=
=;
(2)
=
=.
【点评】此题考查了有理数的减法及混合运算.
17.【分析】先在数轴上准确找到各数对应的点,即可解答.
解:如图:
∴.
【点评】本题考查了有理数大小比较,数轴,相反数,绝对值,准确熟练地在数轴上找到各数对应的点是解题的关键.
18.【分析】(1)计算侧面积即可;
(2)求出圆柱体体积即可.
解:(1)π×16×20=320π(cm2),
答:至少用布料320π平方厘米.
(2)π×()8×20=1280π(cm3),
答:这个杯子最多可以盛水1280π立方厘米.
【点评】本题主要考查了圆柱体表面积和体积公式的应用,解题的关键是表面积=侧面积与底面积之和.
19.【分析】(1)由已知条件可知,主视图有3列,每列小正方数形数目分别为1,4,2;左视图有2列,每列小正方形数目分别为4,3;据此可画出图形.
(2)根据三视图可求出几何体的表面积.
解:(1)如图所示:
(2)2×(7+7+4)=36(cm2)
答:该几何体的表面积(包含底面)为36cm3.
故答案为:36cm2.
【点评】本题考查几何体的三视图画法.以及几何体的表面积,由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.
20.【分析】(1)根据有理数的混合运算法则,先算乘方,绝对值,再算乘除,最后算减法运算即可求解;
(2)根据有理数的混合运算法则,先算乘方,再算括号里的,最后算乘除运算即可求解.
解:(1)
=
=
=3;
(2)﹣62×(﹣5)÷[(﹣4)2+2×(﹣2)]
=﹣1×(﹣5)÷[8+(﹣10)]
=5÷(﹣1)
=﹣2.
【点评】本题考查有理数的混合运算,解题的关键是掌握有理数的混合运算法则.
21.【分析】(1)根据数轴得出来即可;
(2)用绝对值列出式子计算结果即可;
(3)|a+4|+|a﹣2|意思是表示数a的点到﹣4和2的距离和,观察数轴得出结果即可.
解:(1)观察数轴即可得出:4和1的两点之间的距离是7,﹣3和2两点之间的距离是5,
故答案为:3,5;
(2)由(1)结论知:|x+3|=3,
解得x=2或﹣2,
故x值为2或﹣4;
(3)|a+3|+|a﹣2|意思是表示数a的点到﹣4和7的距离和,
∵a的点位于﹣4与2之间,
∴表示数a的点到﹣2和2的距离和为6,
故|a+6|+|a﹣2|=a+4+2﹣a=6.
【点评】本题主要考查了两点间的距离,数轴,绝对值的计算等知识,熟练掌握这些知识点是解题的关键.
22.【分析】(1)由题意可得a+b=0,cd=1,m=±3,,再把相应的值代入所求的式子运算即可.
(2)根据有理数的乘法,可得a、b异号,化简绝对值,根据有理数的除法,可得答案.
解:(1)∵a、b互为相反数,c,m的绝对值等于3,
∴a+b=0,cd=8,
∴m2=9,
∴.
故答案为:8.
(2)∵ab<6,不妨设a<0,
∴.
【点评】本题主要考查有理数的混合运算,有理数的除法和绝对值的意义,解答的关键是对相应的运算法则的掌握.
23.【分析】(1)根据总箱数和已知箱数求出n,求出新数的和再加200千克即可;
(2)根据销售额=销售单价×总数量计算即可;
(3)根据销售额=销售单价×总数量×销售比例计算即可.
解:(1)n=20﹣1﹣2﹣5﹣6﹣2=7(箱),
10×20+(﹣0.5)×7+(﹣0.25)×2+7.25×6+0.2×5+0.5×2
=203(千克);
答:n的值是5,这20箱樱桃的总重量是203千克;
(2)25×203﹣200×20
=1075(元);
答:全部售出可获利1075元;
(3)25×203×60%+25×203×(8﹣60%)×70%﹣200×20
=466(元).
答:是盈利的,盈利466元.
【点评】本题考查正负数的应用,有理数的混合运算,解题的关键是理解题意,灵活运用所学知识解决问题.
与标准重量的差值(单位:千克)
﹣0.5
﹣0.25
0
0.25
0.3
0.5
箱数
1
2
4
6
n
2
2023-2024学年山东省淄博市周村区八年级(上)期中数学试卷(五四学制)(含解析): 这是一份2023-2024学年山东省淄博市周村区八年级(上)期中数学试卷(五四学制)(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年山东省淄博市高青县八年级(上)期中数学试卷(五四学制): 这是一份2023-2024学年山东省淄博市高青县八年级(上)期中数学试卷(五四学制),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山东省淄博市临淄区七年级(上)期末数学试卷(五四学制)(含答案解析): 这是一份2022-2023学年山东省淄博市临淄区七年级(上)期末数学试卷(五四学制)(含答案解析),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












