

2023-2024学年湖南省娄底市双峰县九年级(上)期中数学试卷(含解析)
展开1.下列方程一定是一元二次方程的是( )
A.B.5x2﹣6y﹣3=0
C.ax2﹣x+2=0D.(a2+1)x2+bx+c=0
2.已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
A.=B.=C.=D.=
3.三角形的面积为12cm2,这时底边上的高ycm底边xcm之间的函数关系用图象表示大致是( )
A.B.
C.D.
4.已知线段AB的长度为2,点C是线段AB的黄金分割点,则AC的长度为( )
A.B.C.﹣1或3D.或﹣2
5.用配方法解一元二次方程2x2﹣3x﹣1=0,配方正确的是( )
A.B.
C.D.
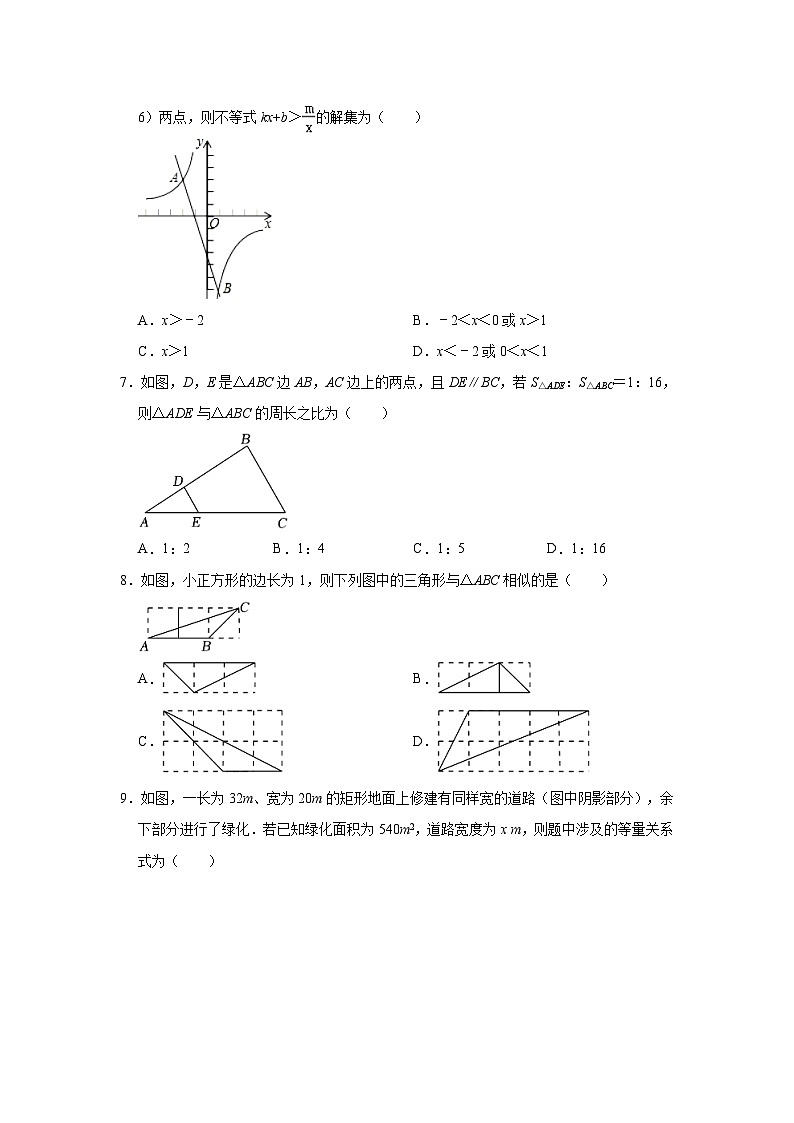
6.如图,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(﹣2,3),B(1,﹣6)两点,则不等式kx+b>的解集为( )
A.x>﹣2B.﹣2<x<0或x>1
C.x>1D.x<﹣2或0<x<1
7.如图,D,E是△ABC边AB,AC边上的两点,且DE∥BC,若S△ADE:S△ABC=1:16,则△ADE与△ABC的周长之比为( )
A.1:2B.1:4C.1:5D.1:16
8.如图,小正方形的边长为1,则下列图中的三角形与△ABC相似的是( )
A.B.
C.D.
9.如图,一长为32m、宽为20m的矩形地面上修建有同样宽的道路(图中阴影部分),余下部分进行了绿化.若已知绿化面积为540m2,道路宽度为x m,则题中涉及的等量关系式为( )
A.(32﹣x)(20﹣x)=540
B.(x﹣32)(20﹣x)=540
C.(x﹣32)(x﹣20)=540
D.(32×24)﹣(32x+20x)=540
10.如图,在平面直角坐标系中,点A在函数y=﹣(x<0)的图象上,点B在函数y=(x>0)的图象上,若AO=2BO,∠AOB=90°,则k的值为( )
A.1B.2C.1.5D.0.25
二、填空题(本大题共6小题,共18分)
11.如果,那么的值等于 .
12.已知x1、x2是一元二次方程x2﹣4x﹣7=0的两个实数根,则的值是 .
13.如图,在△ABC中,D为边AC上的点,连接BD,添加一个条件: ,可以使得△ADB∽△ABC.(只需写出一个)
14.关于x的一元二次方程(m﹣1)x2+3x+m2﹣1=0的一根为0,则m的值是 .
15.反比例函数的图象在第二、四象限,则m的取值范围是 .
16.如图,在△ABC中,AD⊥BC于点D,正方形EFGH的四个顶点都在△ABC的边上,若BC=6cm,AD=4cm,则正方形EFGH的边长是 cm.
三、计算题(每小题6分,共18分)
17.解方程:
(1)x2﹣6x+9=(5﹣2x)2;
(2)2(x﹣2)=x2﹣4.
18.已知某品牌显示器的寿命大约为2×104小时.
(1)这种显示器可工作的天数d与平均每日工作的小时数t之间具有怎样的函数关系?
(2)如果平均每天工作10小时,则这种显示器大约可使用多长时间?
19.已知关于x的方程x2+ax+a﹣2=0.
(1)若该方程的一个根为1,求a的值;
(2)若a的值为3时,请解这个方程.
四、解答题(每小题8分,共16分)
20.如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,=,BF=6cm,求EF和FC的长.
21.已知反比例函数y=(m≠0)与一次函数y=kx+b(k≠0)交于点A(﹣1,6)、B(n,2).
(1)求反比例函数与一次函数的表达式;
(2)若点A关于y轴的对称点为A′,连接AA′,BA′,求△AA′B的面积.
五、解答题(每小题9分,共18分)
22.如图,在平面直角坐标系中,给出了格点△ABC(顶点均在正方形网格的格点上),已知点A的坐标为(﹣4,3).
(1)以点O为位似中心,在给定的网格中画出△A1B1C1,使△ABC与△A1B1C1位似,并且点A1的坐标为(8,﹣6).
(2)△ABC与△A1B1C1的位似比是 .
(3)△A1B1C1的面积是 .
23.“阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种,在双峰县城南郊区李大叔承包了一个葡萄园,种植了大量“阳光玫瑰葡萄”,县城某品牌水果经销商计划在2023年五一期间进行商业促销活动,经过调查往年的统计数据发现,李大叔批发“阳光玫瑰葡萄”的最低价格为每斤15元.若按每斤30元的价格到市区销售,平均每天可售出60斤.若每斤“阳光玫瑰葡萄”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.
(1)若降价2元,则每天的销售利润是多少元?
(2)若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元,那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元?(其它成本忽略不计)
六、综合题(每小题10分,共20分)
24.已知关于x的一元二次方程x2﹣(m﹣3)x﹣m=0.
(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实根为x1、x2,且+﹣x1x2=27,求m的值.
25.如图1,在等腰直角三角形ADC中,∠ADC=90°,AD=4.点E是AD的中点,以DE为边作正方形DEFG,连接AG,CE.将正方形DEFG绕点D顺时针旋转,旋转角为α(0°<α<90°).
(1)如图2,在旋转过程中,
①判断△AGD与△CED是否全等,并说明理由;
②当CE=CD时,AG与EF交于点H,求GH的长.
(2)如图3,延长CE交直线AG于点P.
①求证:AG⊥CP;
②在旋转过程中,线段PC的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
参考答案
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1.下列方程一定是一元二次方程的是( )
A.B.5x2﹣6y﹣3=0
C.ax2﹣x+2=0D.(a2+1)x2+bx+c=0
【分析】找到只含有一个未知数,且未知数的最高次项的次数为2,系数不为0的整式方程即可.
解:A、是分式方程,不合题意;
B、含有2个未知数,不合题意;
C、没有说明a的取值,不合题意;
D、是只含有一个未知数,且未知数的最高次项的次数为2,系数不为0的整式方程,符合题意,
故选:D.
【点评】考查一元二次方程的定义的运用;掌握一元二次方程的准确定义是解决本题的关键;注意a2+1一定是一个正数.
2.已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
A.=B.=C.=D.=
【分析】根据相似三角形的判定和性质定理即可得出结论.
解:∵DE∥BC,EF∥AB,
∴△ADE∽△ABC,△CEF∽△CAB,
∴=,=,==,
故A、B、C选项正确;
∵四边形BDEF是平行四边形,
∴DE=BF,
∴==,故D选项错误;
故选:D.
【点评】本题考查了相似三角形的判定和性质定理;熟练掌握相似三角形的判定和性质是解决问题的关键.
3.三角形的面积为12cm2,这时底边上的高ycm底边xcm之间的函数关系用图象表示大致是( )
A.B.
C.D.
【分析】根据题意有:xy=12;故y与x之间的函数图象为反比例函数,且根据x、y实际意义x、y应大于0,其图象在第一象限;即可得出答案.
解:∵S△=xy=12
∴y=(x>0,y>0)
故选:C.
【点评】本题考查了反比例函数的应用及反比例函数的图象,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
4.已知线段AB的长度为2,点C是线段AB的黄金分割点,则AC的长度为( )
A.B.C.﹣1或3D.或﹣2
【分析】分两种情况讨论:当AC>BC和AC<BC两种情况.
解:∵线段AB=2,点C是线段AB的黄金分割点,
∴当AC>BC时,AC=AB==﹣1,
当AC<BC时,BC=AB==﹣1,
∴AC=AB﹣BC=2﹣(﹣1)=3﹣.
故答案为:﹣1或3﹣.
故选:C.
【点评】本题考查了黄金分割点的定义,熟记黄金分割的定义是解题关键.
5.用配方法解一元二次方程2x2﹣3x﹣1=0,配方正确的是( )
A.B.
C.D.
【分析】移项,系数化成1,再配方,即可得出选项.
解:2x2﹣3x﹣1=0,
2x2﹣3x=1,
x2﹣x=,
x2﹣x+=+,
(x﹣)2=,
故选:C.
【点评】本题考查了解一元二次方程,能正确配方是解此题的关键.
6.如图,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(﹣2,3),B(1,﹣6)两点,则不等式kx+b>的解集为( )
A.x>﹣2B.﹣2<x<0或x>1
C.x>1D.x<﹣2或0<x<1
【分析】结合图象,求出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.
解:∵函数y=kx+b(k≠0)与的图象相交于点A(﹣2,3),B(1,﹣6)两点,
∴不等式的解集为:x<﹣2或0<x<1,
故选:D.
【点评】本题考查了一次函数与反比例函数的交点问题,关键是注意掌握数形结合思想的应用.
7.如图,D,E是△ABC边AB,AC边上的两点,且DE∥BC,若S△ADE:S△ABC=1:16,则△ADE与△ABC的周长之比为( )
A.1:2B.1:4C.1:5D.1:16
【分析】由平行易证△ADE∽△ABC,由面积比等于相似比的平方,周长比等于相似比求解.
解:∵DE∥BC,
∴∠ADE=∠B,
∴△ADE∽△ABC
∵S△ADE:S△ABC=1:16
∴△ADE与△ABC周长之比为1:4,
故选:B.
【点评】本题考查相似三角形的判定和性质,熟练掌握相似三角形性质是解题的关键.
8.如图,小正方形的边长为1,则下列图中的三角形与△ABC相似的是( )
A.B.
C.D.
【分析】根据网格中的数据求出AB,AC,BC的长,求出三边之比,利用三边对应成比例的两三角形相似判断即可.
解:根据题意可得:,∴,
A.三边之比为,图中的三角形(阴影部分)与△ABC不相似.
B.三边之比为,图中的三角形(阴影部分)与△ABC不相似.
C.三边之比为,图中的三角形(阴影部分)与△ABC相似.
D.三边之比为,图中的三角形(阴影部分)与△ABC不相似.
故选:C.
【点评】此题考查了相似三角形的判定,熟练掌握相似三角形的判定方法是解本题的关键.
9.如图,一长为32m、宽为20m的矩形地面上修建有同样宽的道路(图中阴影部分),余下部分进行了绿化.若已知绿化面积为540m2,道路宽度为x m,则题中涉及的等量关系式为( )
A.(32﹣x)(20﹣x)=540
B.(x﹣32)(20﹣x)=540
C.(x﹣32)(x﹣20)=540
D.(32×24)﹣(32x+20x)=540
【分析】若道路宽度为x m,则绿化的部分为长(32﹣x)m,宽(20﹣x)m的矩形,根据绿化的面积为540m2,即可得出关于x的一元二次方程,此题得解.
解:若道路宽度为x m,则绿化的部分为长(32﹣x)m,宽(20﹣x)m的矩形,
依题意得:(32﹣x)(20﹣x)=540.
故选:A.
【点评】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
10.如图,在平面直角坐标系中,点A在函数y=﹣(x<0)的图象上,点B在函数y=(x>0)的图象上,若AO=2BO,∠AOB=90°,则k的值为( )
A.1B.2C.1.5D.0.25
【分析】过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,易得△AOC∽△OBD,然后由相似三角形面积比等于相似比的平方,求得S△AOC:S△BOD=4,继而根据反比例函数系数k的几何意义即可求得答案.
解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
∴∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠BOD=∠OAC,
∴△AOC∽△OBD,
∴S△AOC:S△BOD=()2,
∵AO=2BO,
∴S△AOC:S△BOD=4,
∵点A在函数y=﹣(x<0)的图象上,点B在函数y=(x>0)的图象上,
∴S△AOC=×|﹣4|=2,S△BOD=k,
∴2=4×(k),解得k=1,
故选:A.
【点评】本题主要考查了反比例函数图象上点的坐标特征,相似三角形的判定和性质,反比例函数系数k的几何意义,得到S△AOC:S△BOD=4是解本题的关键.
二、填空题(本大题共6小题,共18分)
11.如果,那么的值等于 .
【分析】根据已知条件得出a=b,再代入要求的式子进行计算即可得出答案.
解:∵=,
∴a=b,
∴==.
故答案为:.
【点评】此题考查了比例的性质,熟练掌握比例的基本性质是解题的关键.
12.已知x1、x2是一元二次方程x2﹣4x﹣7=0的两个实数根,则的值是 .
【分析】根据根与系数的关系得x1+x2=4,x1x2=﹣7,利用代数式变形分别得到,然后利用整体代入的方法计算.
解:根据题意得x1+x2=4,x1x2=﹣7,
===﹣,
故答案为﹣.
【点评】本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=﹣,x1x2=.
13.如图,在△ABC中,D为边AC上的点,连接BD,添加一个条件: ∠ABD=∠C(答案不唯一) ,可以使得△ADB∽△ABC.(只需写出一个)
【分析】根据题意可得已有的条件为∠A=∠A,再添加一个角即可.
解:添加的条件为∠ABD=∠C
∵∠ABD=∠C,∠A=∠A,
∴△ADB∽△ABC,
故答案为:∠ABD=∠C(答案不唯一).
【点评】本题主要考查相似三角形的判定,熟练掌握相似三角形的判定方法是解题关键.
14.关于x的一元二次方程(m﹣1)x2+3x+m2﹣1=0的一根为0,则m的值是 ﹣1 .
【分析】一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值.即把0代入方程求解可得m的值.
解:把x=0代入方程(m﹣1)x2+3x+m2﹣1=0得到m2﹣1=0,
解得:m=±1,
∵m﹣1≠0
∴m=﹣1,
故答案为:﹣1.
【点评】本题考查的是一元二次方程的解的定义,解题的关键是正确的代入求解,属于基础题型.
15.反比例函数的图象在第二、四象限,则m的取值范围是 m>3 .
【分析】根据反比例函数的性质列式计算即可得解.
解:∵反比例函数的图象在第二、四象限,
∴3﹣m<0,
解得m>3.
故答案为:m>3.
【点评】本题考查了反比例函数的性质,对于反比例函数y=(k≠0),(1)k>0,反比例函数图象在一、三象限;(2)k<0,反比例函数图象在第二、四象限内.
16.如图,在△ABC中,AD⊥BC于点D,正方形EFGH的四个顶点都在△ABC的边上,若BC=6cm,AD=4cm,则正方形EFGH的边长是 cm.
【分析】根据EH∥BC求得△AEH∽△ABC,如图设AD与EH交于点M,首先证明四边形EFDM是矩形,设正方形边长为x,再利用△AEH∽△ABC,得=,列出方程即可解决问题.
解:如图设AD与EH交于点M,正方形EFGH的边长为x,
∵四边形EFGH是正方形,
∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C,
∴△AEH∽△ABC.
∴=,
∴=,
∴x=,
∴正方形EFGH的边长为cm.
故答案为:.
【点评】本题考查正方形的性质、相似三角形的判定和性质等知识,解题的关键是利用相似三角形的相似比对于高的比,学会用方程的思想解决问题,属于中考常考题型.
三、计算题(每小题6分,共18分)
17.解方程:
(1)x2﹣6x+9=(5﹣2x)2;
(2)2(x﹣2)=x2﹣4.
【分析】(1)利用完全平方式整理等式左边、再移项然后用平方差公式进行因式分解、最后分别令两个一次式为0,解方程即可;
(2)对等式右边利用平方差公式进行整理、移项后利用提公因式法进行因式分解、最后分别令两个一次式为0,求解方程即可.
解:(1)原方程可化为(x﹣3)2=(5﹣2x)2,
移项得:(x﹣3)2﹣(5﹣2x)2=0,
分解因式得:(x﹣3+5﹣2x)(x﹣3﹣5+2x)=0,
即(2﹣x)(3x﹣8)=0,
∴2﹣x=0或3x﹣8=0,
∴.
(2)原方程可化为2(x﹣2)=(x+2)(x﹣2),
移项得:(x+2)(x﹣2)﹣2(x﹣2)=0,
分解因式得:x(x﹣2)=0,
∴x=0或x﹣2=0,
∴x1=0,x2=2.
【点评】本题考查了解一元二次方程——因式分解,熟练掌握因式分解法解方程是关键.
18.已知某品牌显示器的寿命大约为2×104小时.
(1)这种显示器可工作的天数d与平均每日工作的小时数t之间具有怎样的函数关系?
(2)如果平均每天工作10小时,则这种显示器大约可使用多长时间?
【分析】(1)根据日工作时间乘以天数=总寿命列式即可;
(2)将t=10代入求得的函数解析式即可求得使用时间;
解:(1)∵dt=2×104,
d=;
(2)当t=10时,d==2000,
∴这种显示器大约可使用2000天.
【点评】本题考查了反比例函数的应用,能根据实际问题列出函数关系式是解决本题的关键.
19.已知关于x的方程x2+ax+a﹣2=0.
(1)若该方程的一个根为1,求a的值;
(2)若a的值为3时,请解这个方程.
【分析】(1)将x=1代入原方程可得出关于a的一元一次方程,解之即可得出a的值;
(2)把a=3代入原方程得到x2+3x+1=0,再利用公式法求解即可.
解:(1)将x=1代入原方程,得:1+a+a﹣2=0,
解得:a=;
(2)把a=3代入原方程得,x2+3x+1=0,
∴Δ=32﹣4×1×1=5,
∴x==,
∴x1=,x2=.
【点评】本题考查了一元二次方程的解以及利用公式法解一元二次方程,都是基础知识,需熟练掌握.
四、解答题(每小题8分,共16分)
20.如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,=,BF=6cm,求EF和FC的长.
【分析】根据平行线分线段成比例定理,由AE∥DF得=,可计算出EF=4,则BE=BF+EF=10,然后再由DE∥AC得到=,可计算出CE=,所以CF=CE+EF=.
解:∵AE∥DF,
∴=,即=,
∴EF=4,
∴BE=BF+EF=6+4=10,
∵DE∥AC,
∴=,即=,
∴CE=,
∴CF=CE+EF=.
【点评】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.
21.已知反比例函数y=(m≠0)与一次函数y=kx+b(k≠0)交于点A(﹣1,6)、B(n,2).
(1)求反比例函数与一次函数的表达式;
(2)若点A关于y轴的对称点为A′,连接AA′,BA′,求△AA′B的面积.
【分析】(1)先把A点坐标代入反比例函数y=(m≠0)中求出m的值,进而可得出反比例函数的解析式,再把B点坐标代入即可求出n的值,把A、B两点的坐标代入一次函数y=kx+b中接可求出k、b的值,进而可得出一次函数的解析式;
(2)根据题意求得A′的坐标,然后根据三角形面积公式即可求得.
解:(1)∵反比例函数y=(m≠0)的图象过点A(﹣1,6),
∴6=,即m=﹣6,
∴反比例函数的解析式为:y=﹣;
∵比例函数y=﹣的图象过点B(n,2),
∴2=﹣,解得n=﹣3,
∴B(﹣3,2),
∵一次函数y=kx+b(k≠0)的图象过点A(﹣1,6)和点B(﹣3,2),
∴,解得;
∴一次函数的解析式为:y=2x+8;
(2)∵点A(﹣1,6)关于y轴的对称点为A′,
∴A′(1,6),
∴AA′=2,
∵B(﹣3,2),
∴△AA′B的面积:×2×(6﹣2)=4.
【点评】本题考查的是反比例函数与一次函数的交点问题及三角形的面积公式,熟练掌握待定系数法是解答此题的关键.
五、解答题(每小题9分,共18分)
22.如图,在平面直角坐标系中,给出了格点△ABC(顶点均在正方形网格的格点上),已知点A的坐标为(﹣4,3).
(1)以点O为位似中心,在给定的网格中画出△A1B1C1,使△ABC与△A1B1C1位似,并且点A1的坐标为(8,﹣6).
(2)△ABC与△A1B1C1的位似比是 1:2 .
(3)△A1B1C1的面积是 8 .
【分析】(1)利用点A和A1的坐标特征得到位似比,再把B、C的横纵坐标都乘以﹣2得到B1、C1的坐标,然后描点即可;
(2)由(1)所画图形得到;
(3)利用三角形面积公式计算.
解:(1)如图,△A1B1C1为所作;
(2)△ABC与△A1B1C1的位似比是1:2;
(3)△A1B1C1的面积=×4×4=8.
故答案为1:2;8.
【点评】本题考查了作图﹣位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.
23.“阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种,在双峰县城南郊区李大叔承包了一个葡萄园,种植了大量“阳光玫瑰葡萄”,县城某品牌水果经销商计划在2023年五一期间进行商业促销活动,经过调查往年的统计数据发现,李大叔批发“阳光玫瑰葡萄”的最低价格为每斤15元.若按每斤30元的价格到市区销售,平均每天可售出60斤.若每斤“阳光玫瑰葡萄”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.
(1)若降价2元,则每天的销售利润是多少元?
(2)若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元,那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元?(其它成本忽略不计)
【分析】(1)根据题意,每降低1元,那么平均每天的销售量会增加10斤,若每斤的价格降低2元,则可增加20斤,再根据每斤利润×销量可得解;
(2)根据每天盈利1100元列方程,解出x的值即可求解.
解:(1)根据题意,降价2元则销售量为60+2×10=80(斤),
销售利润为:(30﹣15﹣2)×80=1040(元),
答:若降价2元,则每天的销售利润是1040元;
(2)设每斤“阳光玫瑰葡萄”应降价x元,
根据题意得:(30﹣15﹣x)(60+10x)=1100,
整理得:x2﹣9x+20=0,
解得x1=4,x2=5,
∵为了尽快减少库存,
∴x=5,
此时30﹣x=25,
答:每斤“阳光玫瑰葡萄”的售价应降至每斤25元.
【点评】本题考查了一元二次方程的实际应用问题,能够根据题意列出方程是解题的关键.
六、综合题(每小题10分,共20分)
24.已知关于x的一元二次方程x2﹣(m﹣3)x﹣m=0.
(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实根为x1、x2,且+﹣x1x2=27,求m的值.
【分析】(1)表示出根的判别式,判断其正负即可作出判断;
(2)利用根与系数的关系表示出两根之积与两根之和,已知等式变形代入代入计算即可求出m的值.
【解答】(1)证明:x2﹣(m﹣3)x﹣m=0,
∵Δ=(m﹣3)2﹣4×(﹣m)
=m2﹣6m+9+4m
=m2﹣2m+1+8
=(m﹣1)2+8≥8>0,
∴方程有两个不相等的实数根;
(2)解:由根与系数的关系可得:x1+x2=m﹣3,x1x2=﹣m,
∵+﹣x1x2=27,
∴(x1+x2)2﹣3x1x2=27,即(m﹣3)2+3m=27,
解得:m=﹣3或m=6.
故m的值是﹣3或6.
【点评】此题考查了根与系数的关系,根的判别式,熟练掌握一元二次方程根与系数的关系是解本题的关键.
25.如图1,在等腰直角三角形ADC中,∠ADC=90°,AD=4.点E是AD的中点,以DE为边作正方形DEFG,连接AG,CE.将正方形DEFG绕点D顺时针旋转,旋转角为α(0°<α<90°).
(1)如图2,在旋转过程中,
①判断△AGD与△CED是否全等,并说明理由;
②当CE=CD时,AG与EF交于点H,求GH的长.
(2)如图3,延长CE交直线AG于点P.
①求证:AG⊥CP;
②在旋转过程中,线段PC的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
【分析】(1)①结论:△AGD≌△CED.根据SAS证明即可.
②如图2中,过点A作AT⊥GD于T.解直角三角形求出AT,GT,再利用相似三角形的性质求解即可.
(2)①如图3中,设AD交PC于O.利用全等三角形的性质,解决问题即可.
②因为∠CPA=90°,AC是定值,推出当∠ACP最小时,PC的值最大,推出当DE⊥PC时,∠ACP的值最小,此时PC的值最大,此时点F与P重合(如图4中).
解:(1)①如图2中,结论:△AGD≌△CED.
理由:∵四边形EFGD是正方形,
∴DG=DE,∠GDE=90°,
∵DA=DC,∠ADC=90°,
∴∠GDE=∠ADC,
∴∠ADG=∠CDE,
∴△AGD≌△CED(SAS).
②如图2中,过点A作AT⊥GD于T.
∵△AGD≌△CED,CD=CE,
∴AD=AG=4,
∵AT⊥GD,
∴TG=TD=1,
∴AT==,
∵EF∥DG,
∴∠GHF=∠AGT,
∵∠F=∠ATG=90°,
∴△GFH∽△ATG,
∴=,
∴=,
∴GH=.
(2)①如图3中,设AD交PC于O.
∵△AGD≌△CED,
∴∠DAG=∠DCE,
∵∠DCE+∠COD=90°,∠COD=∠AOP,
∴∠AOP+∠DAG=90°,
∴∠APO=90°,
∴CP⊥AG.
②∵∠CPA=90°,AC是定值,
∴当∠ACP最小时,PC的值最大,
∴当DE⊥PC时,∠ACP的值最小,此时PC的值最大,此时点F与P重合(如图4中),
∵∠CED=90°,CD=4,DE=2,
∴EC===2,
∵EF=DE=2,
∴CP=CE+EF=2+2,
∴PC的最大值为2+2.
【点评】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是正确寻找全等三角形解决问题,学会寻找特殊位置解决最值问题,属于中考压轴题.
2023-2024学年湖南省娄底市双峰县八年级(上)学期期末数学试题(含解析): 这是一份2023-2024学年湖南省娄底市双峰县八年级(上)学期期末数学试题(含解析),共15页。试卷主要包含了选择题,填空题,解答题,应用题,操作与说理等内容,欢迎下载使用。
湖南省娄底市双峰县2023-2024学年九年级上学期期中数学试题: 这是一份湖南省娄底市双峰县2023-2024学年九年级上学期期中数学试题,共11页。试卷主要包含了如图,函数等内容,欢迎下载使用。
湖南省娄底市双峰县2023-2024学年九年级上学期期中数学试题: 这是一份湖南省娄底市双峰县2023-2024学年九年级上学期期中数学试题,共10页。试卷主要包含了如图,函数等内容,欢迎下载使用。












