中职数学7.1 数列的概念完美版练习题习题ppt课件

这是一份中职数学7.1 数列的概念完美版练习题习题ppt课件，文件包含高教版2021中职数学拓展模块二下册71数列的概念课件pptx、高教版2021中职数学拓展模块二下册71数列的概念教案docx、高教版2021中职数学拓展模块二下册71数列的概念课内习题答案docx等3份课件配套教学资源，其中PPT共26页， 欢迎下载使用。

7.1 数列的概念
数列是刻画客观事物规律性的一种数学模型，在生产实践和科学研究中有着广泛的应用.
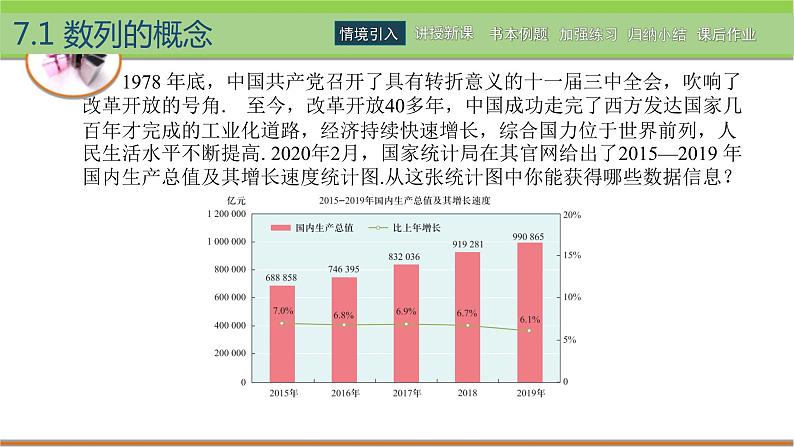
1978 年底，中国共产党召开了具有转折意义的十一届三中全会，吹响了改革开放的号角. 至今，改革开放40多年，中国成功走完了西方发达国家几百年才完成的工业化道路，经济持续快速增长，综合国力位于世界前列，人民生活水平不断提高. 2020年2月，国家统计局在其官网给出了2015—2019 年国内生产总值及其增长速度统计图.从这张统计图中你能获得哪些数据信息？
根据图中的数据，把这五年的国内生产总值依次排成一列 688858，746395，832036，919281，990865； （1） 相应的年份可以排成一列 2015，2016，2017，2018，2019； （2） 每一年的增长率也可以排成一列 7.0%，6.8%，6.9 % ，6.7 % ，6.1 % ； （3）
像(1)(2)(3)这样按照一定次序排成的一列数称为数列.数列中的每一个数为这个数列的项.
数列的一般形式为a1，a2，a3，…，an，…，简记作an ．其中， a1称为数列的首项， an称为数列的第n项，n称为项数.
例如，某种细菌每经过时间t分裂一次，每次分裂都是1个细菌分裂成2个 . 这样，每次分裂之后的细菌总数可以构成一个数列 2，4，8，16，32，…， （4）其中 a1=2，a2=4，a3=8，…. 无穷多个3排成的 数列 3，3，3，3，3，… （5）其中 a1=3，a2=3，a3=3，….
项数有限的数列称为有穷数列，项数无限的数列称为无穷数列．例如，数列(1)、(2)、(3)是有穷数列，数列(4)、(5)是无穷数列．像数列(5)这样所有项均为同一个数的数列叫做常数列．
一般地，当一个数列的第n项an与项数n之间的关系可以用一个式子来表示时，这个式子就称为这个数列的通项公式. 
分析发现，数列(4)的每一项都可以写成以2为底的指数幂，其第1项a1 = 21，第2项a2 = 22 ， …，第n项为an = 2n. 同样，数列(2)也有一定的规律，其第1项为a1 = 2014+1,第2 项a2 = 2014+2 ，… ，第n项. 
例如，数列(2)的通项公式是an = 2014+n；数列(4)的通项公式是an = 2n.
不是所有的数列都有通项公式.如数列(1)、(2)、(3)就没有通项公式.
根据通项公式，写出下列数列an 的前5项
写出数列{an}的一个通项公式，使它的前4项分别是下列各数.
（1）2，4，6，8；
（1）因为数列的前4项2，4，6，8都等于相应项数的2倍，所以它的一个通项公式是an＝2n；
设数列an 的通项公式是an=3n+1，问13是否为该数列的项？若是，它数列的是第几项？
设13是数列{an}的第n项，将13代入数列的通项公式an=3n+1中，得13=3n+1，解得 n=4.因此，13是数列{an}中的项 ，并且它是数列的第4项．
已知数列an的首项a1=3，n≥2时，an＝an-1+2 ，试写出这个数列的前5项．
想一想，这个数列相邻两项的差有什么特点？
若数列有通项公式，则可以利用这个通项公式求出数列的各项．对于有些没有通项公式的数列，有时可以借助数列中相邻项的关系来确定数列的各项．
1.书本作业：完成课后练习题和习题；2.复习巩固：复习已学内容;3.提升作业：学有余力的同学做一做扩展延伸内容.