








中职数学7.4 等差数列与等比数列的应用优质练习题习题ppt课件
展开7.4 等差数列与等比数列的应用
等差数列与等比数列的知识在日常生活和工农业生产中有着 广泛的应用,如投资理财、货品堆积统计、企业调查、职场应聘等.我们可以通过建立数学模型,用等差数列和等比数列知识来解决这些实际问题.
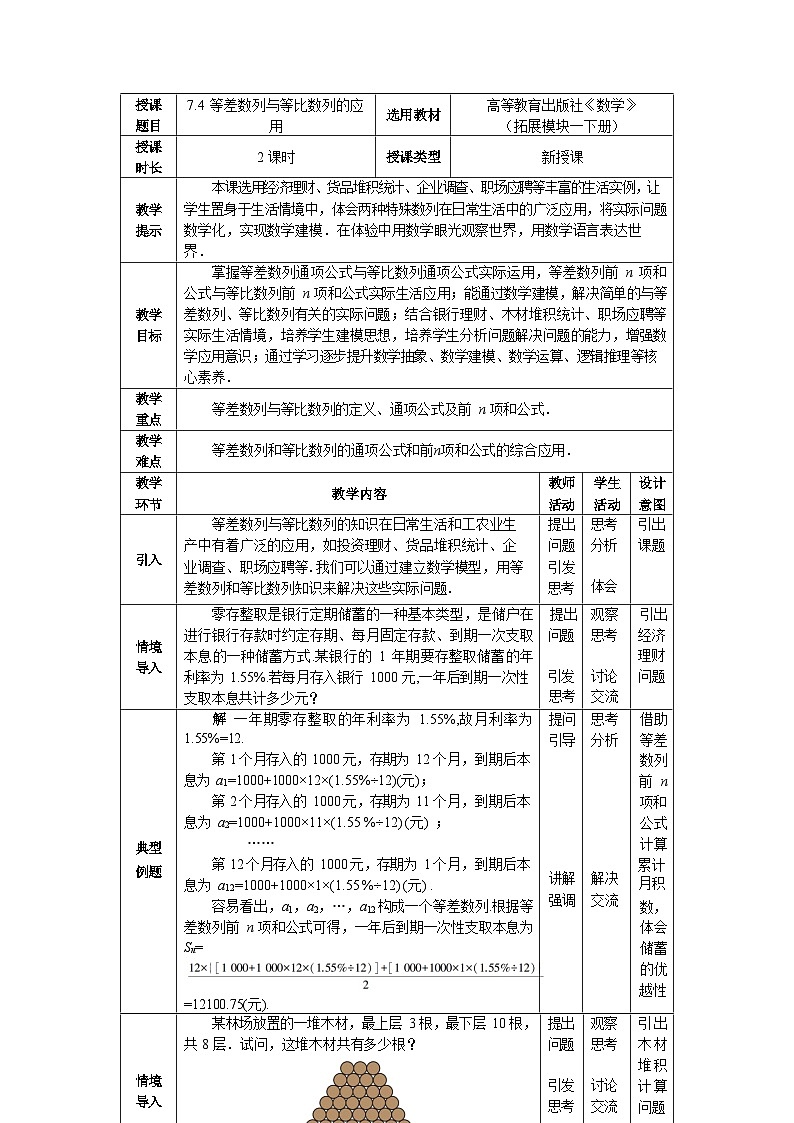
零存整取是银行定期储蓄的一种基本类型,是储户在进行银行存款时约定存期、每月固定存款、到期一次支取本息的一种储蓄方式.某银行的1年期零存整取储蓄的年利率为1.55%.若每月存入银行1000元,一年后到期一次性支取本息共计多少元?
教育储蓄是指个人按国家有关规定在指定银行开户、存入规定数额资金、用于教育目的的专项储蓄,是一种专门为学生支付非义务教育所需教育金的专项储蓄.教育储蓄是一种零存整取定期储蓄存款,与普通储蓄相比,教育储蓄具有利率优惠(按零存整取存入但享受整存整取的利率)和利息免税的优点. 如果把“情境与问题(1)”中的零存整取储蓄换成教育储蓄,而一年期整存整取的年利率为1.75%,在其他条件不变的情况下, 则一年到期后一次性支取本息和为 =12113.75(元).
某林场放置的一堆木材,最上层3根,最下层10根,共8层.试问,这堆木材共有多少根?
两位同学分别到甲、乙两家公司应聘,均被录用.甲公司承诺第一年年薪是50000元,以后每年比上一年加薪5000元.乙公司承诺第一年的年薪是50000元,以后每年的年薪比上一年增加10%.假设聘期为五年,试问 (1)应聘到甲公司的同学,其第五年的年薪是多少?五年的总收入是多少? (2)应聘到乙公司的同学,其第五年的年薪是多少?五年的总收入是多少?
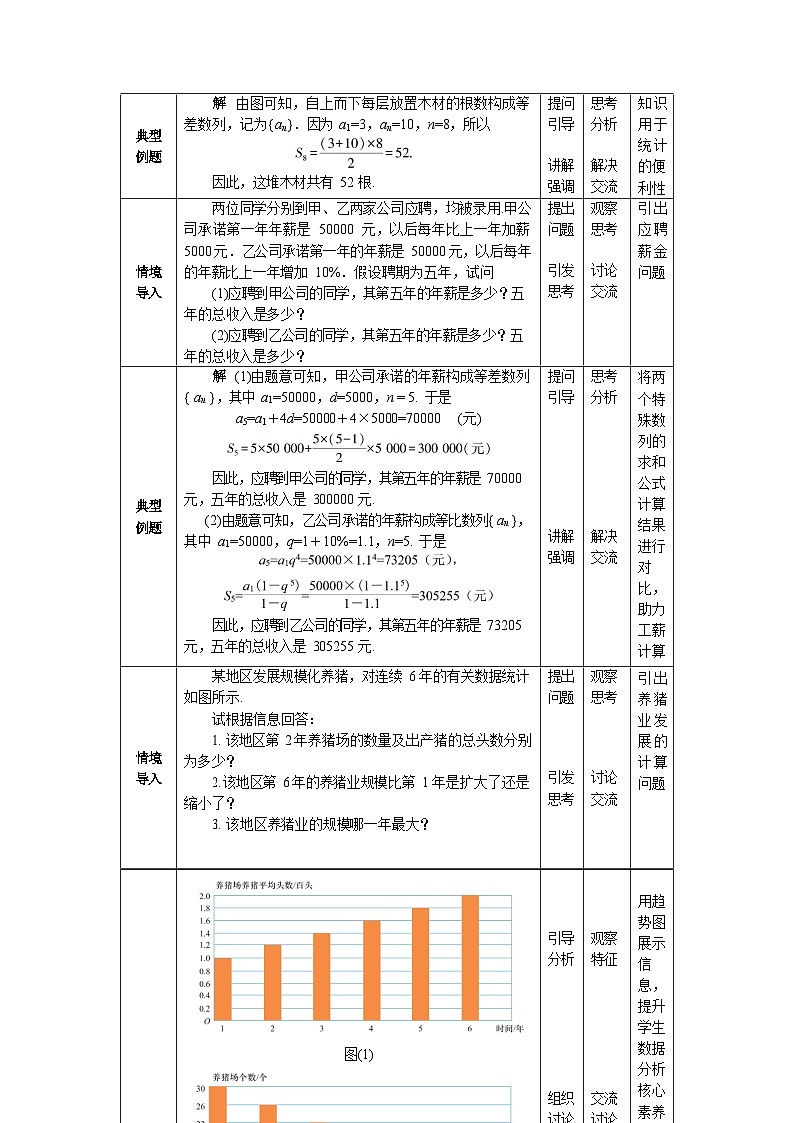
某地区发展规模化养猪,对连续6年的有关数据统计如图所示.
图(1) 图(2)试根据上述信息回答: 1. 该地区第2年养猪场的数量及出产猪的总头数分别为多少? 2.该地区第6年的养猪业规模比第1年是扩大了还是缩小了? 3. 该地区养猪业的规模哪一年最大?
养猪总头数=养猪场平均出产头数×养猪场数量. 由图(1)可看出,从第1年到第6年,该地区养猪场出产猪的平均头数成等差数列上升;由图(2)可看出,养猪场的数量成等差数列下降.
2.第1年出产猪的总头数S1=100×30=3000(头),第6年出产猪的总头数 S6=200×10=2000 (头). 因为2000<3000,所以,第6 年该地区养猪业的规模比第1年缩小了.
3. 在图(1)中,设第n年养猪场的平均出产头数为an ,则有 an=100+20×(n-1)=80+20n (n=1,2,3,4,5,6). 在图(2)中,设第n年养猪场数量为bn ,则有 bn=30-4×(n-1)=34-4n (n=1,2,3,4,5,6).由此可见,第n年出产的猪总头数为 anbn=(80+20n)(34-4n)=2720+360n-80n² =-80(n-2)²+3120 (n=1,2,3,4,5,6). 当n=2时,anbn最大,即第2年养猪规模最大,且最大值为3120头.
1.某种细菌每30分钟分裂一次(一个分裂为两个),问一个细菌3h后分裂成多少个? 2.某人通过社交软件分别向5位好友发出加入某环保活动的一级邀请,5位好友中的每人再向各自的5位好友发出加入此环保活动的二级邀请,如此进行下去.试问,经过四级邀请接到邀请的人数是多少(假设邀请和加入的人员不同)?
1.书面作业:完成课后习题和《学习指导与练习》;2.查漏补缺:根据个人情况对课堂学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.
高教版(2021)拓展模块二 下册9.2 正态分布优秀练习题习题ppt课件: 这是一份高教版(2021)拓展模块二 下册9.2 正态分布优秀练习题习题ppt课件,文件包含高教版2021中职数学拓展模块二下册92正态分布课件pptx、高教版2021中职数学拓展模块二下册92正态分布教案docx、高教版2021中职数学拓展模块二下册92正态分布课内习题答案docx等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
中职数学高教版(2021)拓展模块二 下册8.1.1 分类计数原理练习题课件ppt: 这是一份中职数学高教版(2021)拓展模块二 下册8.1.1 分类计数原理练习题课件ppt,文件包含高教版2021中职数学拓展模块二下册81计数原理课件pptx、高教版2021中职数学拓展模块二下册81计数原理教案docx、高教版2021中职数学拓展模块二下册81计数原理课内习题答案docx等3份课件配套教学资源,其中PPT共26页, 欢迎下载使用。
中职数学高教版(2021)拓展模块二 下册7.3 等比数列优秀练习题习题课件ppt: 这是一份中职数学高教版(2021)拓展模块二 下册7.3 等比数列优秀练习题习题课件ppt,文件包含高教版2021中职数学拓展模块二下册73等比数列课件pptx、高教版2021中职数学拓展模块二下册73等比数列教案docx、高教版2021中职数学拓展模块二下册73等比数列课内习题答案docx等3份课件配套教学资源,其中PPT共31页, 欢迎下载使用。













