浙教版七年级下册1.4平行线的性质教学ppt课件

这是一份浙教版七年级下册1.4平行线的性质教学ppt课件，共14页。PPT课件主要包含了复习旧知，探索新知，平行线的性质1，几何语言，性质和判定的比较，同位角相等，两直线平行，角的相等，由“线”定“角”，由“角”定“线”等内容，欢迎下载使用。

判断两直线平行的常用方法有哪几种？
同位角相等，两直线平行。
内错角相等，两直线平行。
同旁内角互补，两直线平行。
这些判定方法的条件是什么，结果是什么？
1、 ∵ ∠B＝∠1， ∴ AD//BC（ ）2、 ∵ ∠1＝∠D， ∴ AB//CD（ ）3、 ∵ ∠B+∠BCD＝180， ∴ __________（ ）4、 ∵ ∠2=∠4， ∴ __________（ ）5、 ∵ _______＝_______， ∴ AB//CD（ ）
同位角相等，两直线平行
内错角相等，两直线平行
同旁内角互补，两直线平行
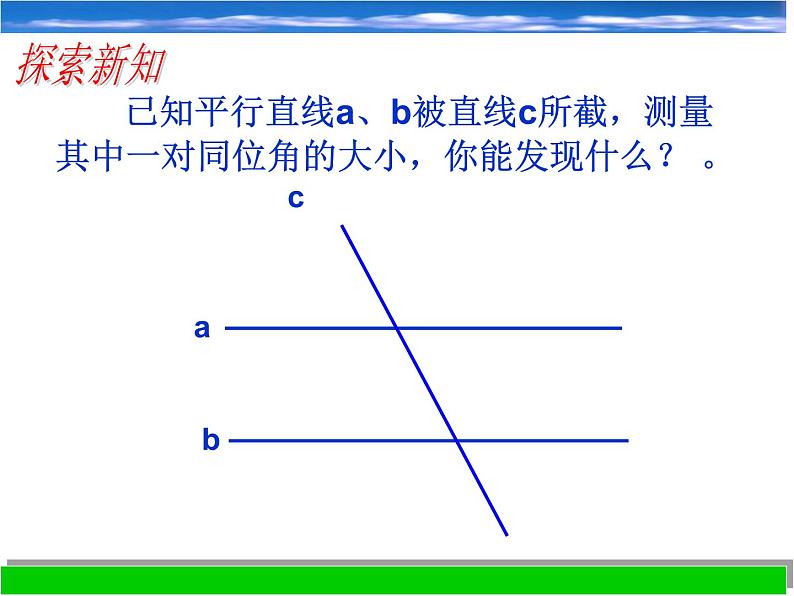
已知平行直线a、b被直线c所截，测量其中一对同位角的大小，你能发现什么？ 。
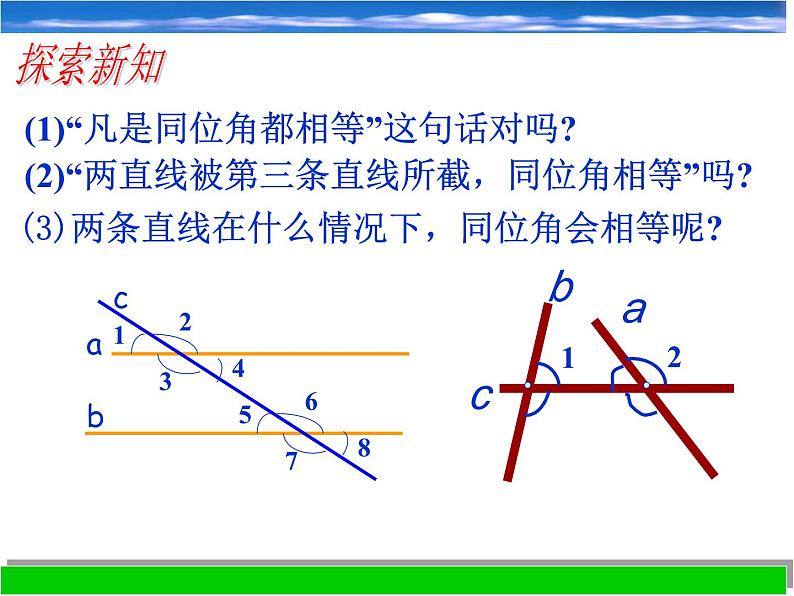
(1)“凡是同位角都相等”这句话对吗?
(2)“两直线被第三条直线所截，同位角相等”吗?
(3)两条直线在什么情况下，同位角会相等呢?
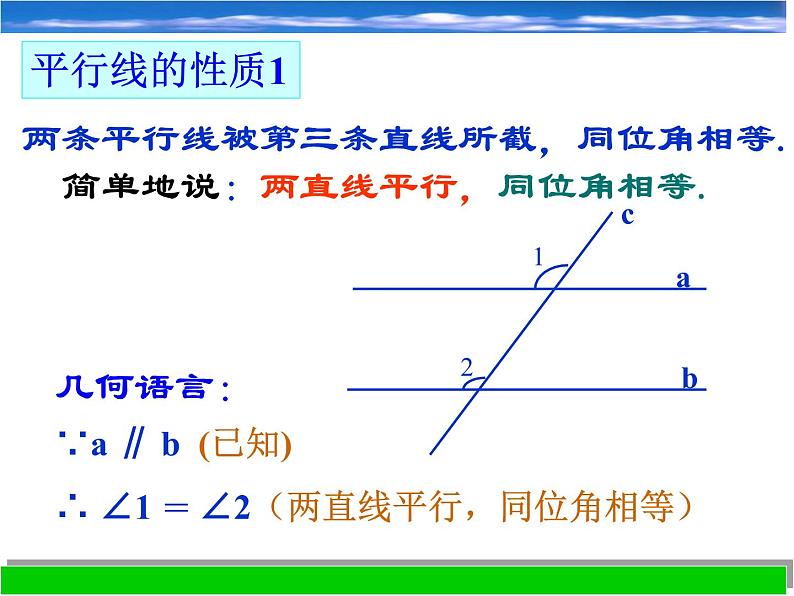
两条平行线被第三条直线所截，同位角相等. 简单地说：两直线平行，同位角相等.
∵a ∥ b (已知)∴ ∠1 ＝ ∠2（两直线平行，同位角相等）
两条直线被第三条直线所截
条件 结论
1、判定与性质的条件与结论有什么关系？
2、使用判定时: 已知 说明 ；
使用性质时: 已知_____________说明___________。
由“线”的位置关系（平行）
由“角”的数量关系（相等）
定“线”的位置关系（平行）
定“角”的数量关系（相等）
如图，梯子的各条横档互相平行，∠1＝100，求∠2的度数。
例2 如图,已知∠1=∠2,若直线b⊥m,则直线a⊥m,请说明理由.
如图所示 ∠3=∠4 ，求证：∠1=∠2 .
如图，已知BE平分∠ABC, ∠1＝∠2, 试说明∠AED=∠C
如图，已知AE//CF，AB//CD，∠A＝40，求∠C的度数。