广西专版2023_2024学年新教材高中物理第3章相互作用__力4力的合成和分解课时1力的合成和分解课件新人教版必修第一册

这是一份广西专版2023_2024学年新教材高中物理第3章相互作用__力4力的合成和分解课时1力的合成和分解课件新人教版必修第一册，共60页。

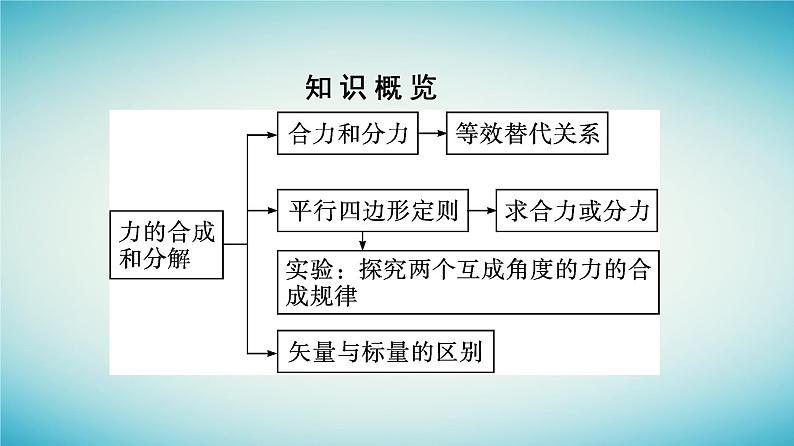
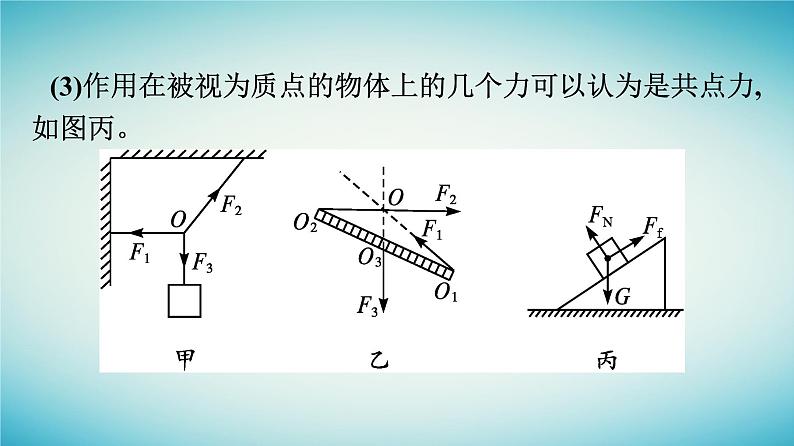
4　力的合成和分解课时1　力的合成和分解素养·目标定位课前·基础认知课堂·重难突破随 堂 训 练素养·目标定位目 标 素 养1.知道共点力的概念,能从力的作用效果上理解合力和分力,知道合力与分力的大小关系,形成正确的物理观念。2.知道力的合成和分解的概念,明白力的合成与力的分解是等效替代关系,培养科学思维能力。3.掌握平行四边形定则或三角形定则计算合力或分力。4.知道矢量和标量的区别。5.实验:探究两个互成角度的力的合成规律,培养实验探究能力。知 识 概 览 课前·基础认知一、共点力1.定义:几个力如果都作用在物体的　同一点　,或者它们的作用线　相交　于一点,这几个力叫作共点力。 2.共点力的几种情况。(1)几个力同时作用于同一点,如图甲。(2)几个力的作用线的延长线能够相交于同一点,如图乙。(3)作用在被视为质点的物体上的几个力可以认为是共点力,如图丙。微思考1观察三个图中的作用力,哪个是共点力?提示:甲图中,三个力共同作用在物体同一点上;乙图中,三个力虽然不作用在同一点上,但它们的作用线交于一点,所以甲、乙两图中的三个力为共点力。丙图中的力既没有作用在同一点上,它们的作用线也不交于一点,是非共点力。二、合力和分力1.合力与分力:假设一个力单独作用的效果跟某几个力共同作用的效果相同,这个力就叫作那几个力的　合力　。假设几个力共同作用的效果跟某个力单独作用的效果相同,这几个力就叫作那个力的　分力　。 2.合力与分力的关系:合力与分力之间的关系是一种　等效替代　的关系,合力作用的效果与分力共同作用的效果相同。 微思考2《曹冲称象》:时孙权曾致巨象,太祖欲知其斤重,访之群下,咸莫能出其理。冲曰:“置象大船之上,而刻其水痕所至,称物以载之,则校可知矣。”故事中,大象与石头的重力有什么关系?类比体会合力与分力的关系。提示:在船的吃水线相同的情况下,一头大象的重力与一堆石头的重力相当。其中包含了等效替代的思想方法,即一头大象和一堆石头的作用效果相同。合力与分力的关系就是一种等效替代关系。三、力的合成和分解1.力的合成:求几个力的　合力　的过程叫作力的合成。 2.力的分解:求一个力的　分力　的过程叫作力的分解。 3.平行四边形定则:两个力合成时,如果以表示这两个力的有向线段为邻边作平行四边形,这两个邻边之间的　对角线　就代表合力的大小和方向。如图所示,　F　表示F1与F2的合力。 4.力的分解法则:力的分解也遵从平行四边形定则。如果没有限制,同一个力F可以分解为　无数　对大小、方向不同的分力。一个已知力究竟应该怎样分解,要根据具体问题来确定。 5.两个以上共点力的合力的求法:先求出任意两个力的合力,再求出这个合力与第三个力的合力,直到把　所有的力　都合成进去,最后得到的结果就是这些力的合力。 微判断(1)合力与分力同时作用在一个物体上。(　　)(2)由作出的力的平行四边形定则可知,合力可能小于分力。(　　)(3)共点力一定作用于物体上的同一点。(　　)(4)把已知力F分解为两个分力F1与F2,此时物体受到F、F1、F2三个力的作用。(　　)×√××四、矢量和标量1.矢量:既有大小又有方向,相加时遵从　平行四边形定则　(或三角形定则)的物理量。 2.标量:只有大小,没有方向,相加时遵从　算术法则　的物理量。 3.三角形定则:把两个矢量首尾相接,从第一个矢量的始端指向第二个矢量的末端的有向线段就表示合矢量的大小和方向。课堂·重难突破一 合力与分力的关系重难归纳1.合力与分力的三性。2.合力与分力的大小关系。 3.三个力合力范围的确定。 如图甲所示,把物块挂在一个弹簧测力计的下面,稳定时弹簧测力计的示数为F;如图乙所示,用两个弹簧测力计(方向不同)拉住同一物块,稳定时弹簧测力计示数分别为F1、F2。F与F1、F2有什么关系?F1、F2两个数值相加正好等于F吗?当图乙中两弹簧测力计夹角从一个较小的角度逐渐增大到很大时,图乙中两个弹簧测力计的示数F1、F2与F的大小关系怎样变化?提示:F与F1、F2作用效果相同,可等效替代。F1、F2数值相加不等于F。当题图乙中两个弹簧测力计夹角由较小逐渐增大到很大的过程中,F1、F2的大小逐渐增大,并且由开始数值比F小增大为比F大。典例剖析【例1】 (多选)下列说法正确的是(　　)A.两个力的合力可能小于一个分力B.5 N、2 N、6 N三个共点力的最大合力为13 N,最小合力为1 NC.两个分力的大小和方向都被确定,则合力也被确定D.合力与分力是同时作用于物体上的力答案:AC解析:根据平行四边形定则,两个力的合力可能比分力大,也可能比分力小,故选项A正确;5 N、2 N、6 N中前两力的合力范围为3 N≤F12≤7 N,6 N的力在前两个力的范围之内,故三个力的合力的最小值为0,故选项B错误;两个分力的大小和方向都被确定,根据平行四边形定则可知,合力的大小和方向是一定的,故选项C正确;合力与分力只是效果相同,并不是物体同时受到的力,故选项D错误。方法规律求n个力的合力的最小值的方法找出其中的最大者F0,求出其他(n-1)个力的大小之和为F'。若F0≤F',则n个合力的最小值Fmin=0;若F0>F',则n个力合力的最小值Fmin=F0-F'。学以致用1.(多选)两个共点力F1、F2大小不同,它们的合力大小为F,则(　　)A.F1、F2同时增大一倍,F也增大一倍B.F1、F2同时增大10 N,F也增大10 NC.F1增大10 N,F2减小10 N,F一定不变D.若F1、F2中的一个增大,F不一定增大答案:AD规律总结合力大小的分析方法(1)两个分力大小确定时,其合力的大小范围由两分力之间的夹角决定。夹角越大合力越小。(2)两个分力方向确定时,其合力的大小范围由两分力之间的大小决定。当夹角θ<90°时,分力增大时合力一定增大;当θ>90°时,分力增大时合力不一定增大。(3)合力大小可由图解法分析。二 求合力的大小重难归纳1.作图法。根据平行四边形定则用作图工具作出平行四边形,然后用测量工具测量出合力的大小、方向,具体操作过程如下:2.计算法。作平行四边形,再根据正、余弦定理,三角函数,几何知识等计算合力。具体过程如下:3.求合力的几种特例。 特别提醒在力的合成中分力是实际存在的,每一个分力都有对应的施力物体,而合力没有与之对应的施力物体。两人同拉一辆车,如图所示,每人都用100 N的力拉,车受到的拉力一定是200 N吗?提示:不一定。两个力的合力不一定等于两个力大小之和,应根据平行四边形定则,用作图或者计算的方法求得合力。典例剖析【例2】如图所示,水平地面上固定着一根竖直立柱,某人用细绳通过柱顶的光滑定滑轮将重100 N的货物拉住。已知人拉着细绳的一端,且该细绳端与水平方向的夹角为30°,则柱顶所受细绳的压力大小为(　　)答案:B 解析:以货物为研究对象,根据二力平衡可知,细绳的拉力为100 N,所以滑轮两侧细绳的拉力F1=F2=100 N。根据平行四边形定则作出滑轮两侧细绳拉力的合力F,如图所示。 根据几何关系可知,柱顶所受细绳的压力大小规律总结(1)作图法“五要”:①分力、合力要共点;②实线、虚线要分清;③分力、合力标度要相同;④作图要准确;⑤对角线要找准。(2)计算法求合力常用知识:①应用直角三角形关系;②应用等边三角形特点;③应用相似三角形知识。学以致用2.杨浦大桥是继南浦大桥之后又一座跨越黄浦江的我国自行设计建造的双塔双索面迭合梁斜拉桥,如图所示。挺拔高耸的208 m主塔似一把利剑直刺苍穹,塔的两侧32对钢索连接主梁,呈扇面展开,如巨型琴弦,正弹奏着巨龙腾飞的奏鸣曲。假设斜拉桥中某对钢索与竖直方向的夹角都是30°,每根钢索中的拉力都是3×104 N,那么它们对塔柱形成的合力有多大?方向如何?答案:5.2×104 N,方向竖直向下 解析:把两根钢索的拉力看成沿钢索方向的两个分力,以它们为邻边画出一个平行四边形,其对角线就表示它们的合力。由对称性可知,合力方向一定沿塔柱竖直向下。下面用两种方法计算这个合力的大小。方法一:作图法(如图甲所示)。自O点引两根有向线段OA和OB,它们跟竖直方向的夹角都为30°。取单位长度为1×104 N,则OA和OB的长度都是3个单位长度。量得对角线OC长为5.2个单位长度,所以合力的大小为F=5.2×1×104 N=5.2×104 N。方法二:计算法(如图乙所示)。根据这个平行四边形是一个菱形的特点,如图乙所示,连接AB,交OC于D,则AB与OC互相垂直平分,三 力的分解重难归纳1.按实际效果分解。根据实际问题中力的作用效果,确定出两个分力的方向,画出力的平行四边形,进行分解的方法。其解题基本思路可表示为:2.按实际需要进行分解。实际问题中,一个力的作用效果可有多个理解的角度,这种情况下要根据题目要求,按实际需要进行分解。3.有关力的分解的讨论。力分解时是有解还是无解,关键是看代表合力的对角线与给定的代表分力的有向线段是否能构成平行四边形(或三角形)。若可以构成平行四边形(或三角形),说明合力可以分解成给定的分力,即有解;若不能,则无解。常见的有四种分解情况:4.力的正交分解法。 我们不可能直接用双手把一段圆木掰成两半,但若我们使用斧子,就很容易将圆木向两边劈开(如图甲、乙)。仔细观察你会发现,斧子的横截面就像是两个背靠背黏合在一起的斜面。斧子这种独特的形状能够将一个较小的力分解成两个较大的分力。想一想,这是什么原因呢?提示:当合力一定时,分力的大小和方向将随着分力间夹角的改变而改变。两个分力间的夹角越大,分力也就越大(如图甲、乙)。刀、斧等工具正是利用了这一道理。将刀、斧的刃做薄,使其锋利;将其背适当做厚,使劈开物体的分力之间的夹角较大,产生的分力也就较大。典例剖析 答案:AD 解析:因Fsin 30°