人教版七年级上册1.3.2 有理数的减法精品课件ppt

这是一份人教版七年级上册1.3.2 有理数的减法精品课件ppt，共6页。PPT课件主要包含了有理数的减法法则，有理数减法法则，减号变加号，减数变其相反数，被减数不变，例1计算，有理数的减法运算，归纳总结，–08，–47等内容，欢迎下载使用。

你听说过国家级森林公园抱犊崮吗？
已知抱犊崮某日山下温度为5 ℃，山上温度为–5 ℃，你能列式表示出山上温度与山下温度的温差吗？
1. 理解有理数减法的意义.
2. 掌握有理数减法法则，熟练进行有理数的减法运算.
3. 经历有理数减法法则的探索过程，体会有理数减法与加法的关系.
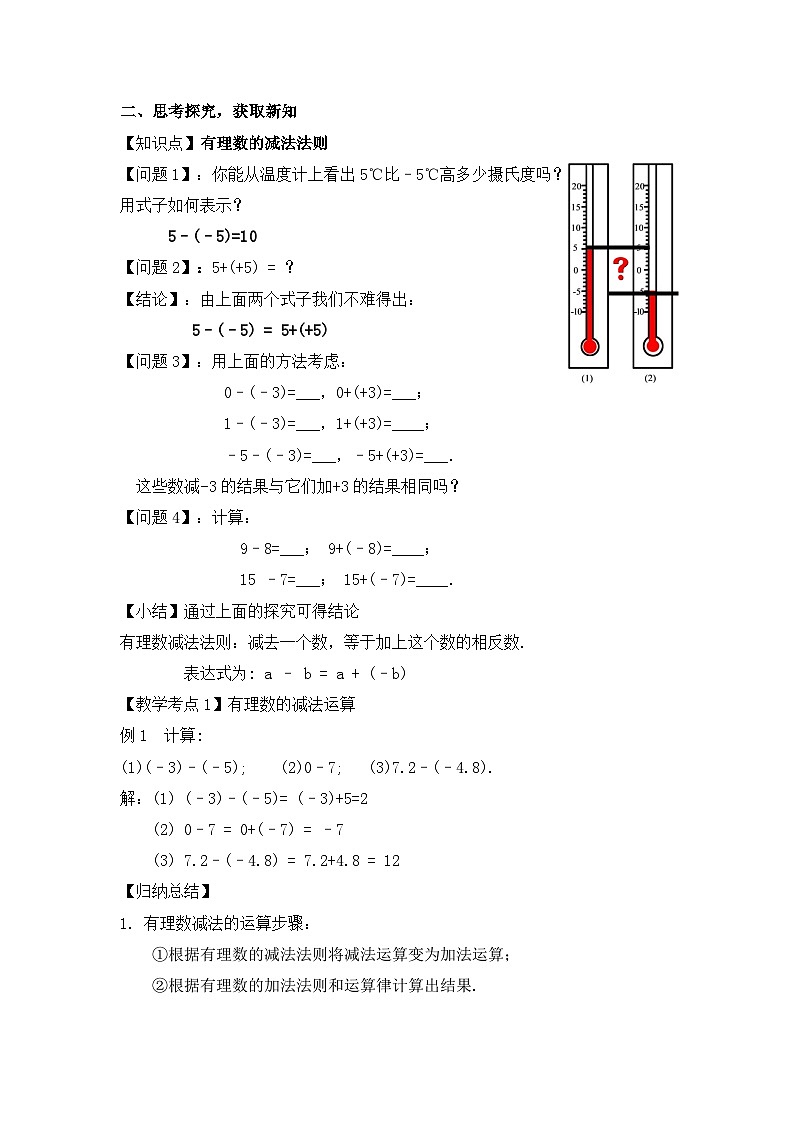
问题1：你能从温度计上看出5℃比–5℃高多少摄氏度吗？用式子如何表示？问题2： 5+(+5) = ？结论：由上面两个式子我们不难得出：
5–(–5)=10
5–(–5) = 5+(+5)
问题3：用上面的方法考虑：　 0–(–3)=___，0+(+3)=___； 　 1–(–3)=___，1+(+3)=____；　 –5–(–3)=___，–5+(+3)=___．问题4：计算： 9–8=___； 9+(–8)=____； 15 –7=___； 15+(–7)=____．
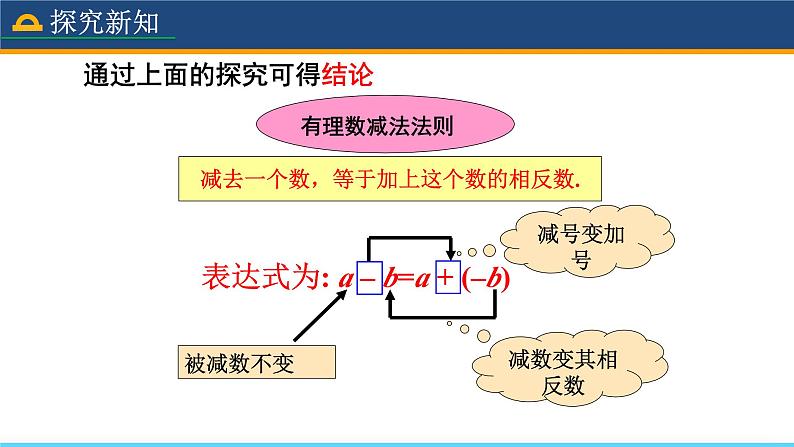
减去一个数，等于加上这个数的相反数.
表达式为: a – b=a + (–b)
通过上面的探究可得结论
(1)(–3)–(–5); (2)0–7; (3)7.2–(–4.8).
解：(1) (–3)–(–5)= (–3)+5=2
(2) 0–7 = 0+(–7) = –7
(3) 7.2–(–4.8) = 7.2+4.8 = 12
1. 有理数减法的运算步骤：①根据有理数的减法法则将减法运算变为加法运算；②根据有理数的加法法则和运算律计算出结果.2. 有理数的减法是有理数加法的逆运算 ，在转化过程中，应注意“两变一不变”，即减法变加法、减数变成它的相反数、被减数不变.
3. 有理数减法运算的四种情况： （1）任意一个数减去一个正数等于加上一个负数，如a-b=a+(-b); （2）任意一个数减去一个负数等于加上一个正数，如a-(-b)=a+b； （3）任何一个数减去0仍得这个数，如a-0=a; （4）0减去 一个数等于这个数的相反数，如0-a=-a.
填空：（1）–4 –(–3.2)= –4+ = ； （2）(–35)–(+12)= . 计算（口答） （1）6–9； （2）(+4)–(–7)； （3）(–5)–(–8) ； （4）(–4)–9； （5）0–(–5)；   （6）0–5．
例2 已知│a│= 5，│b│= 3，且a>0，b<0， 则a–b= .
解析：由│a│= 5，│b│= 3，得a=± 5，b= ±3. 又因为a>0，b<0，所以a= 5，b= –3. 所以a–b=5–(–3)=5+3=8.
有理数的减法的分类讨论题
若x是2的相反数，|y|＝3，则x–y的值是(　　) A．–5 B．1 C．–1或5 D．1或–5
解析：∵x是2的相反数，∴x= –2. ∵|y|＝3， ∴y=±3， 当y=3时，x–y= –2–3= –2+(–3)= –5； 当y= –3时，x–y= –2–(–3)= –2+3=1，故选D.
例3 世界上最高的山峰是珠穆朗玛峰，其海拔高度是 8844 米，吐鲁番盆地的海拔高度是–155 米，两处高度相差多少米？
解：8844 –(–155) =8844+155 =8999（米）答：两处高度相差8999米.
以地面为基准，A处高+2.5 m，B处高–17.8 m，C处高–32.4 m.问： （1）A处比B处高多少? （2）B处和C处哪个地方高?高多少? （3）A处和C处哪个地方低?低多少?
解：（1）(+2.5)–(–17.8)=2.5+17.8=20.3（m）. （2） B处高，(–17.8)–(–32.4)=–17.8+32.4=14.6（m）. （3） C处低，(+2.5)–(–32.4)=2.5+32.4=34.9（m）.
例4 某日哈尔滨、长春等五个城市的最高气温与最低气温记录如下表. 哪个城市的温差最大？哪个城市的温差最小？
分析：温差即最高气温与最低气温的差． 首先要根据题意列式，利用法则求解，最后比较大小．解：哈尔滨的温差为 2–(–12)＝2＋(＋12)＝14（ ℃ ）， 长春的温差为 3–(–10)＝3＋(＋10)＝13（ ℃ ）， 沈阳的温差为 3–(–8)＝3＋(＋8)＝11 （ ℃ ）， 北京的温差为 12–2＝10 （ ℃ ）， 大连的温差为 6–(–2)＝6＋(＋2)＝8（ ℃ ）．答：五个城市中哈尔滨的温差最大，为14 ℃； 大连的温差最小，为8 ℃.
小明家蔬菜大棚内的气温是24℃，此时棚外的气温是–13℃. 棚内气温比棚外气温高多少摄氏度？
解：24 –(–13)= 24+13=37（℃）
答：棚内气温比棚外高37℃.
1. –3–（–2）的值是（　　） A．–1 B．1 C．5 D．–5
2. 比–1小2的数是（　　） A．3 B．1 C．–2 D．–3
解析：–1–2= –3.
解析：–3–（–2）= –3+2= –1．
（1）(+7) –(–4); （2）(–0.45)–(–0.55);（3） 0–(–9)； （4） (–4)– 0 ；（5）(–5)–(+3).
（1）温度4℃比–6℃高________℃ ； （2）温度–7℃比–2℃低_________℃ ； （3）海拔高度–13m比–200m高_______m； （4）从海拔20m到–40m，下降了______m.
3. 判断并说明理由.（1）在有理数的加法中，两数的和一定比加数大.（ ）（2）两个数相减，被减数一定比减数大.（ ）（3）两数之差一定小于被减数.（ ）（4）0减去任何数，差都为负数.（ ）（5）较大的数减去较小的数，差一定是正数.（ ）
也可能小于加数或等于加数，例如–2+（–3）=–5，–3+0=–3.
也可能小于减数或相等，例如–4–10；6–6.
也可能大于被减数或相等，例如–4–（–10）=6；6–0=6.
也可能是正数或0，例如0–0=0，0–（–2）=2.
某次法律知识竞赛中规定：抢答题答对一题得20分，答错一题扣10分，问答对一题与答错一题得分相差多少分？
20–(–10)=20+10=30 (分)
答：答对一题与答错一题相差30分.
已知|x|＝3，|y|＝5，且|x–y|＝|x|＋|y|，求x＋y和x–y的值．
解：∵|x–y|＝|x|＋|y|， ∴x与y异号或x，y中至少有一个为0， 又|x|＝3，|y|＝5， ∴x＝3时，y＝–5；x＝–3时，y＝5. 当x＝3，y＝–5时，x＋y＝3＋(–5)＝–2，x–y＝3–(–5)＝8； 当x＝–3，y＝5时，x＋y＝–3＋5＝2，x–y＝–3–5＝–8.
有理数减法法则：减去一个数，等于加上这个数的 相反数．