2023-2024学年甘肃省兰州市教育局第四片区联考八年级（上）期中数学试卷（含解析）

这是一份2023-2024学年甘肃省兰州市教育局第四片区联考八年级（上）期中数学试卷（含解析），共1页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。

1．下列各组线段中，不能构成直角三角形的是（ ）
A．3，4，5B．5，12，13C．8，15，17D．6，7，9
2．在﹣2，，，3.14，，，这6个数中，无理数共有（ ）
A．4个B．3个C．2个D．1个
3．若点P（a+2，a）在y轴上，则点P的坐标为（ ）
A．（﹣2，0）B．（0，﹣2）C．（2，0）D．（0，2）
4．的算术平方根是（ ）
A．4B．2C．±4D．±2
5．点P关于x轴对称点M的坐标为（4，﹣5），那么点P关于y轴对称点N的坐标为（ ）
A．（﹣4，5）B．（4，5）C．（﹣4，﹣5）D．（﹣5，4）
6．估计的值在（ ）
A．1和2之间B．2和3之间C．3和4之间D．4和5之间
7．下列函数①y＝﹣5x；②y＝﹣2x+1；③y＝；④y＝x+6；⑤y＝x2﹣1中是一次函数的有（ ）
A．1个B．2个C．3个D．4个
8．已知+|b﹣1|＝0．那么（a+b）2023的值为（ ）
A．﹣1B．1C．32023D．﹣32023
9．在△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，根据以下条件：①∠A+∠B＝∠C；②a：b：c＝3：4：5；③a2＝c2﹣b2；④∠A：∠B：∠C＝1：2：3；⑤a＝32，b＝42，c＝52； ⑥a＝，b＝，c＝．能判定△ABC为直角三角形的有（ ）
A．①②③⑤B．②③④⑤C．①②③④D．①②③④⑤⑥
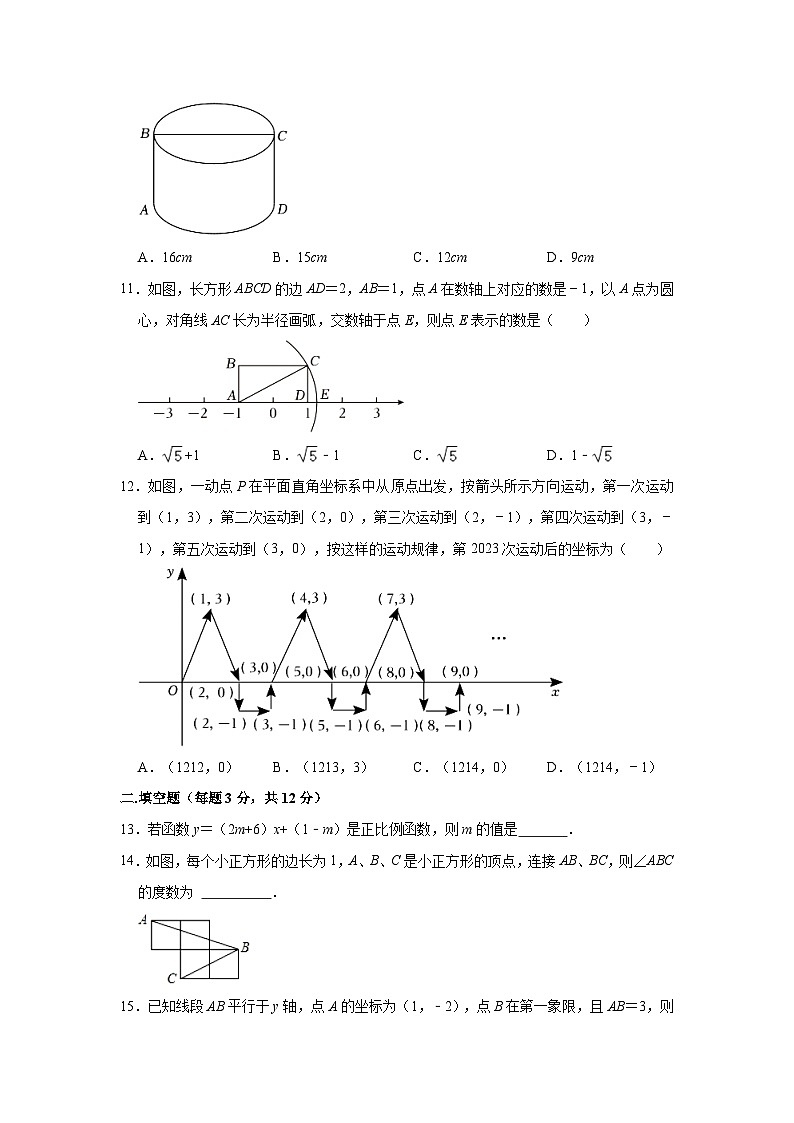
10．如图，圆柱的底面周长为24cm，高AB为9cm，BC是底面直径，一只蚂蚁从点A出发沿着圆柱体的侧面爬行到点C的最短路程是（ ）
A．16cmB．15cmC．12cmD．9cm
11．如图，长方形ABCD的边AD＝2，AB＝1，点A在数轴上对应的数是﹣1，以A点为圆心，对角线AC长为半径画弧，交数轴于点E，则点E表示的数是（ ）
A．+1B．﹣1C．D．1﹣
12．如图，一动点P在平面直角坐标系中从原点出发，按箭头所示方向运动，第一次运动到（1，3），第二次运动到（2，0），第三次运动到（2，﹣1），第四次运动到（3，﹣1），第五次运动到（3，0），按这样的运动规律，第2023次运动后的坐标为（ ）
A．（1212，0）B．（1213，3）C．（1214，0）D．（1214，﹣1）
二.填空题（每题3分，共12分）
13．若函数y＝（2m+6）x+（1﹣m）是正比例函数，则m的值是 ．
14．如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，连接AB、BC，则∠ABC的度数为 ．
15．已知线段AB平行于y轴，点A的坐标为（1，﹣2），点B在第一象限，且AB＝3，则点B的坐标为 ．
16．任何实数a，可用[a]表示不超过a的最大整数，如[4]＝4，[]＝1．现对72进行如下操作：72[]＝8[]＝2[]＝1，这样对72只需进行3次操作后变为1，类似的，①对81只需进行 次操作后变为1；②只需进行3次操作后变为1的所有正整数中，最大的是 ．
三、解答题（共10小题，满分72分）
17．计算：
（1）（﹣1）2023+﹣π0+×；
（2）÷﹣×+．
18．已知x+3的立方根为2，3x+y﹣1的平方根为±4，求x+2y的算术平方根．
19．先化简，后求值：，其中．
20．我们规定用（a，b）表示一对数对，给出如下定义：记m＝，n＝（a＞0，b＞0），将（m，n）与（n，m）称为数对（a，b）的一对“对称数对”．例如（4，1）的一对“对称数对”为（2，1）与（1，2）．
（1）数对（25，4）的一对“对称数对”是 和 ；
（2）若数对（x，2）的一对“对称数对”的一个数对是（，3），求x的值．
21．如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为17米，此人以1米每秒的速度收绳，7秒后船移动到点D的位置，问船向岸边移动了多少米？（假设绳子是直的）
22．甲、乙两地相距200km，现有一列火车从乙地出发，以80km/h的速度向甲地行驶．设x（h）表示火车行驶的时间，y（km）表示火车于甲地的距离．
（1）写出y与x之间的关系式，并判断y是否为x的一次函数；
（2）当x＝1.5时，求y的值．
23．如图，学校有一块四边形的空地ABCD，为了绿化环境，计划在空地上种植草皮，经测量，∠ADC＝90°，CD＝3m，AD＝4m，AB＝13m，BC＝12m．
（1）求出空地ABCD的面积．
（2）若每种植1m2草皮需要200元，问总共需投入多少元？
24．如图，△ABC的三边分别为AC＝6，BC＝8，AB＝10，如果将△ABC沿AD折叠，使AC恰好落在AB边上．
（1）试判断△ABC的形状，并说明理由．
（2）求线段CD的长．
25．如图，在直角坐标系中有三点A（﹣2，3）、B（2，1）、C（3，3）．
（1）在平面直角坐标系中画出△ABC；
（2）求△ABC的面积；
（3）P是x轴上的动点，求PA+PB的最小值．
26．如图1，长方形OABC的边OA、OC分别在x轴、y轴上，B点坐标是（8，4），将△AOC沿对角线AC翻折得△ADC，AD与BC相交于点E．
（1）求证：△CDE≌△ABE
（2）求E点坐标；
（3）如图2，动点P从点A出发，沿着折线A→B→C→O运动（到点O停止），是否存在点P，使得△POA的面积等于△ACE的面积，若存在，直接写出点P坐标，若不存在，说明理由．
参考答案
一、选择题（每题3分，共36分。在每小题列出的选项中，选出正确的一项）
1．下列各组线段中，不能构成直角三角形的是（ ）
A．3，4，5B．5，12，13C．8，15，17D．6，7，9
【分析】根据勾股定理的逆定理和各个选项中的数据，可以判断各个选项中的数据是否可以组成直角三角形，本题得以解决．
解：32+42＝52，故选项A不符合题意；
52+122＝132，故选项B不符合题意；
82+152＝172，故选项C不符合题意；
62+72≠92，故选项D符合题意；
故选：D．
【点评】本题考查勾股定理的逆定理，解答本题的关键是明确题意，利用勾股定理的逆定理解答．
2．在﹣2，，，3.14，，，这6个数中，无理数共有（ ）
A．4个B．3个C．2个D．1个
【分析】要确定题目中的无理数，在明确无理数的定义的前提下，知道无理数分为3大类：π类，开方开不尽的数，无限不循环的小数，根据这3类就可以确定无理数的个数．从而得到答案．
解：根据判断无理数的3类方法，可以直接得知：
是开方开不尽的数是无理数，
属于π类是无理数，
因此无理数有2个．
故选：C．
【点评】本题考查了无理数的定义，判断无理数的方法，要求学生对无理数的概念的理解要透彻．
3．若点P（a+2，a）在y轴上，则点P的坐标为（ ）
A．（﹣2，0）B．（0，﹣2）C．（2，0）D．（0，2）
【分析】根据y轴上的点的坐标特点可得a+2＝0，再解即可．
解：∵点P（a+2，a）在y轴上，
所以点P的横坐标为0，即a+2＝0，
解得a＝﹣2，
则点P的坐标是（0，﹣2），
故选：B．
【点评】此题主要考查了点的坐标，关键是掌握y轴上的点的横坐标为0．
4．的算术平方根是（ ）
A．4B．2C．±4D．±2
【分析】利用算术平方根的意义解答即可．
解：∵＝4，4的算术平方根为2，
∴的算术平方根是2，
故选：B．
【点评】本题主要考查了算术平方根的意义，熟练掌握算术平方根的意义是解题的关键．
5．点P关于x轴对称点M的坐标为（4，﹣5），那么点P关于y轴对称点N的坐标为（ ）
A．（﹣4，5）B．（4，5）C．（﹣4，﹣5）D．（﹣5，4）
【分析】根据关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数，即点P（x，y）关于x轴的对称点P′的坐标是（x，﹣y）．关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变，即点P（x，y）关于y轴的对称点P′的坐标是（﹣x，y）．
解：∵点P关于x轴对称点M的坐标为（4，﹣5），
∴P（4，5），
∴点P关于y轴对称点N的坐标为：（﹣4，5）．
故选：A．
【点评】此题主要考查了关于坐标轴对称的点的性质，正确记忆横纵坐标关系是解题的关键．
6．估计的值在（ ）
A．1和2之间B．2和3之间C．3和4之间D．4和5之间
【分析】根据算术平方根的定义，估算无理数的大小即可．
解：∵32＝9，42＝16，而9＜15＜16，
∴，
即3＜＜4，
故选：C．
【点评】本题考查估算无理数的大小，掌握算术平方根的定义是正确解答的前提．
7．下列函数①y＝﹣5x；②y＝﹣2x+1；③y＝；④y＝x+6；⑤y＝x2﹣1中是一次函数的有（ ）
A．1个B．2个C．3个D．4个
【分析】根据一次函数的定义，对题目中给出的函数逐一进行判断即可得出答案．
解：①y＝﹣5x是一次函数（正比例函数）；
②y＝﹣2x+1是一次函数；
③y＝是反比例函数；
④y＝x+6是一次函数；
⑤y＝x2﹣1是二次函数．
综上所述：①②④是一次函数，共3个．
故选：C．
【点评】此题主要考查了一次函数的定义，熟练掌握一次函数的定义是解决问题的关键．
8．已知+|b﹣1|＝0．那么（a+b）2023的值为（ ）
A．﹣1B．1C．32023D．﹣32023
【分析】根据算术平方根、绝对值的非负性，求出a、b的值，再代入计算即可．
解：∵+|b﹣1|＝0．
∴a+2＝0，b﹣1＝0，
即a＝﹣2，b＝1，
∴（a+b）2023＝（﹣2+1）2023＝﹣1，
故选：A．
【点评】本题考查算术平方根、绝对值，理解算术平方根、绝对值的非负性是正确解答的前提．
9．在△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，根据以下条件：①∠A+∠B＝∠C；②a：b：c＝3：4：5；③a2＝c2﹣b2；④∠A：∠B：∠C＝1：2：3；⑤a＝32，b＝42，c＝52； ⑥a＝，b＝，c＝．能判定△ABC为直角三角形的有（ ）
A．①②③⑤B．②③④⑤C．①②③④D．①②③④⑤⑥
【分析】根据三角形内角和定理可分析出①④的正误；根据勾股定理逆定理可分析出②③⑥的正误，根据三角形的三边关系可以分析出⑤的正误．
解：①∠A+∠B＝∠C，∠A+∠B+∠C＝180°，
∴∠C＝90°，
∴△ABC为直角三角形，故符合题意；
②a：b：c＝3：4：5，
设a＝3x，b＝4x，c＝5x，
∵（3x）2+（4x）2＝（5x）2，
∴能构成直角三角形，故符合题意；
③a2＝c2﹣b2，
∴a2+b2＝c2，
∴能构成直角三角形，故符合题意；
④∠A：∠B：∠C＝1：2：3；
设∠A＝x，∠B＝2x，∠C＝3x，
∵∠A+∠B＝x+2x＝3x＝∠C，∠A+∠B+∠C＝180°，
∴∠C＝90°，
∴能构成直角三角形，故符合题意；
⑤a＝32，b＝42，c＝52，
∵a+b＝c，
∴不能构成三角形，
∴不能构成直角三角形，故不符合题意；
⑥a＝，b＝，c＝，，，
∵，
∴不能构成直角三角形，故不符合题意；
能构成直角三角形的是①②③④．
故选：C．
【点评】此题主要考查了直角三角形的判定和三角形的三边关系，关键是掌握勾股定理逆定理：如果三角形的三边长a，b，c满足a2+b2＝c2，那么这个三角形就是直角三角形．
10．如图，圆柱的底面周长为24cm，高AB为9cm，BC是底面直径，一只蚂蚁从点A出发沿着圆柱体的侧面爬行到点C的最短路程是（ ）
A．16cmB．15cmC．12cmD．9cm
【分析】将圆柱的侧面展开，得到一个长方形，再然后利用两点之间线段最短解答．
解：如图所示：
由于圆柱体的底面周长为24cm，
则AD＝24×＝12（cm），
又因为CD＝AB＝9cm，
所以AC＝＝＝15（cm）．
故蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是15cm，
故选：B．
【点评】此题主要考查了平面展开图﹣最短路径问题，将圆柱的侧面展开，构造出直角三角形是解题的关键．
11．如图，长方形ABCD的边AD＝2，AB＝1，点A在数轴上对应的数是﹣1，以A点为圆心，对角线AC长为半径画弧，交数轴于点E，则点E表示的数是（ ）
A．+1B．﹣1C．D．1﹣
【分析】首先根据勾股定理计算出AC的长，进而得到AE的长，再根据A点表示﹣1，可得点E表示的实数．
解：∵AD长为2，AB长为1，
∴AC＝，
∵A点表示﹣1，
∴点E表示的实数是﹣1．
故选：B．
【点评】此题主要考查了勾股定理的应用，关键是掌握勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
12．如图，一动点P在平面直角坐标系中从原点出发，按箭头所示方向运动，第一次运动到（1，3），第二次运动到（2，0），第三次运动到（2，﹣1），第四次运动到（3，﹣1），第五次运动到（3，0），按这样的运动规律，第2023次运动后的坐标为（ ）
A．（1212，0）B．（1213，3）C．（1214，0）D．（1214，﹣1）
【分析】根据题中所给的点P的运动方式，发现纵坐标为3的这些点与运动次数之间的关系即可解决问题．
解：由题知，
点P第一次运动到（1，3），
点P第六次运动到（4，3），
点P第十一次运动到（7，3），
…，
由此可见，点P第（5n﹣4）次运动到的点的坐标为（3n﹣2，3）（n为正整数）．
当n＝405时，
5n﹣4＝2021，3n﹣2＝1213，
即点P第2021次运动后的坐标为（1213，3）．
所以P第2023次运动后的坐标为（1214，﹣1）．
故选：D．
【点评】本题考查点的坐标变化规律，能根据点P的运动方式得出点P第（5n﹣4）次运动到的点的坐标为（3n﹣2，3）（n为正整数）是解题的关键．
二.填空题（每题3分，共12分）
13．若函数y＝（2m+6）x+（1﹣m）是正比例函数，则m的值是 1 ．
【分析】根据正比例函数的定义列出关于m的不等式组，求出m的值即可．
解：∵函数y＝（2m+6）x+（1﹣m）是正比例函数，
∴，解得m＝1．
故答案为：1．
【点评】本题考查的是正比例函数的定义，熟知一般地，形如y＝kx（k是常数，k≠0）的函数叫做正比例函数是解答此题的关键．
14．如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，连接AB、BC，则∠ABC的度数为 45° ．
【分析】分别在格点三角形中，根据勾股定理即可得到AB，BC，AC的长度，继而可得出∠ABC的度数．
解：
连接AC．
根据勾股定理可以得到：AC＝BC＝，AB＝，
∵+＝，即AC2+BC2＝AB2，
∴△ABC是等腰直角三角形．
∴∠ABC＝45°．
故答案为：45°．
【点评】本题考查了勾股定理，判断△ABC是等腰直角三角形是解决本题的关键，注意在格点三角形中利用勾股定理．
15．已知线段AB平行于y轴，点A的坐标为（1，﹣2），点B在第一象限，且AB＝3，则点B的坐标为 （1，1） ．
【分析】由段AB平行于y轴可得xB＝1，由AB＝3可得|﹣2﹣yB|＝3，以此求得yB的值，并结合点B在第一象限求解即可．
解：∵线段AB平行于y轴，点A的坐标为（1，﹣2），
∴xB＝1，
∵AB＝3，
∴|﹣2﹣yB|＝3，
解得：yB＝1或﹣5，
又∵点B在第一象限，
∴yB＝1，
∴B（1，1）．
故答案为：（1，1）．
【点评】本题主要考查坐标与图形性质，熟知平行于y轴的直线上的点的横坐标相同是解题关键．
16．任何实数a，可用[a]表示不超过a的最大整数，如[4]＝4，[]＝1．现对72进行如下操作：72[]＝8[]＝2[]＝1，这样对72只需进行3次操作后变为1，类似的，①对81只需进行 3 次操作后变为1；②只需进行3次操作后变为1的所有正整数中，最大的是 255 ．
【分析】①根据规律依次求出即可；
②要想确定只需进行3次操作后变为1的所有正整数，关键是确定二次操作后数的大小不能大于4，二次操作时根号内的数必须小于16，而一次操作时正整数255恰好满足这一条件，即最大的正整数为255．
解：①[]＝9，[]＝3，[]＝1，
故答案为：3；
②最大的是255，
[]＝15，[]＝3，[]＝1，而[]＝16，[]＝4，[]＝2，[]＝1，
即只需进行3次操作后变为1的所有正整数中，最大的正整数是255，
故答案为：255．
【点评】本题考查了估算无理数的大小的应用，主要考查学生的阅读能力和猜想能力．
三、解答题（共10小题，满分72分）
17．计算：
（1）（﹣1）2023+﹣π0+×；
（2）÷﹣×+．
【分析】（1）先利用乘方和零指数幂的意义计算，再根据二次根式的乘法法则运算，然后化简二次根式后合并即可；
（2）先根据二次根式的除法法则和乘法法则运算，然后化简二次根式后合并即可．
解：（1）原式＝﹣1+3﹣1+
＝﹣1+3﹣1+2
＝3；
（2）原式＝﹣+2
＝4﹣+2
＝4+．
【点评】本题考查了二次根式的混合运算，熟练掌握二次根式的性质、二次根式的乘法和除法法则和零指数幂是解决问题的关键．
18．已知x+3的立方根为2，3x+y﹣1的平方根为±4，求x+2y的算术平方根．
【分析】根据立方根及平方根的定义求得x，y的值，然后将其代入x+2y中计算后利用算术平方根的定义即可求得答案．
解：∵x+3的立方根为2，3x+y﹣1的平方根为±4，
∴x+3＝8，3x+y﹣1＝16，
解得：x＝5，y＝2，
则x+2y＝5+4＝9，
那么x+2y的算术平方根是3．
【点评】本题考查平方根，算术平方根及立方根，结合已知条件求得x，y的值是解题的关键．
19．先化简，后求值：，其中．
【分析】先按照二次根式混合运算的法则把原式进行化简，然后将代入计算即可．
解：
＝a2﹣5﹣a2+2a
＝2a﹣5，
将代入2a﹣5得，
＝2+2﹣5
＝．
【点评】本题考查了二次根式的化简求值、平方差公式计算，掌握二次根式混合运算的法则是解题关键．
20．我们规定用（a，b）表示一对数对，给出如下定义：记m＝，n＝（a＞0，b＞0），将（m，n）与（n，m）称为数对（a，b）的一对“对称数对”．例如（4，1）的一对“对称数对”为（2，1）与（1，2）．
（1）数对（25，4）的一对“对称数对”是 （5，2） 和 （2，5） ；
（2）若数对（x，2）的一对“对称数对”的一个数对是（，3），求x的值．
【分析】（1）根据新定义及算术平方根的定义即可求得答案；
（2）根据新定义即可求得答案．
解：（1）∵＝5，＝2，
∴（25，4）的一对“对称数对”是（5，2）和（2，5），
故答案为：（5，2）；（2，5）；
（2）由题意可得x＝32＝9．
【点评】本题考查新定义及算术平方根，熟练掌握其定义是解题的关键．
21．如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为17米，此人以1米每秒的速度收绳，7秒后船移动到点D的位置，问船向岸边移动了多少米？（假设绳子是直的）
【分析】在Rt△ABC中，利用勾股定理计算出AB长，再根据题意可得CD长，然后再次利用勾股定理计算出AD长，再利用BD＝AB﹣AD可得BD长．
解：在Rt△ABC中：
∵∠CAB＝90°，BC＝17米，AC＝8米，
∴AB＝＝15（米），
∵此人以1米每秒的速度收绳，7秒后船移动到点D的位置，
∴CD＝17﹣1×7＝10（米），
∴AD＝＝＝6（米），
∴BD＝AB﹣AD＝15﹣6＝9（米），
答：船向岸边移动了9米．
【点评】此题主要考查了勾股定理的应用，关键是掌握从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．
22．甲、乙两地相距200km，现有一列火车从乙地出发，以80km/h的速度向甲地行驶．设x（h）表示火车行驶的时间，y（km）表示火车于甲地的距离．
（1）写出y与x之间的关系式，并判断y是否为x的一次函数；
（2）当x＝1.5时，求y的值．
【分析】（1）根据火车到甲地的距离＝甲、乙间的距离﹣火车行驶的路程，列出函数关系式，再根据一次函数的定义判断即可；
（2）将x＝1.5代入（1）中所求函数解析式可得．
解：（1）根据题意得：y＝200﹣80x，
根据一次函数的定义，y是x的一次函数，
∴y与x之间的关系式y＝200﹣80x，y是x的一次函数；
（2）当x＝015时，y＝200﹣80×1.5＝80．
∴y的值为80．
【点评】本题主要考查利用一次函数的模型解决实际问题的能力．要先根据题意列出函数关系式．解题的关键是要分析题意根据实际意义求解．
23．如图，学校有一块四边形的空地ABCD，为了绿化环境，计划在空地上种植草皮，经测量，∠ADC＝90°，CD＝3m，AD＝4m，AB＝13m，BC＝12m．
（1）求出空地ABCD的面积．
（2）若每种植1m2草皮需要200元，问总共需投入多少元？
【分析】（1）连接AC，由勾股定理得AC2＝52（m2），再由勾股定理的逆定理证△ABC是直角三角形，∠ACB＝90°，然后求出S四边形ABCD＝S△ACB﹣S△ACD＝24（m2），即可求解．
（2）根据空地ABCD的面积和每种植1m2草皮需要200元，列式计算即可．
解：（1）连接AC，如图：
在Rt△ACD中，AC2＝CD2+AD2＝32+42＝52（m2），
在△ABC中，AB2＝132（m2），BC2＝122（m2），
∵52+122＝132，
∴AC2+BC2＝AB2，
∴△ABC是直角三角形，∠ACB＝90°，
∴S四边形ABCD＝S△ACB﹣S△ACD＝•AC•BC﹣AD•CD＝×5×12﹣×3×4＝24（m2）；
（2）∵每平方米草皮需200元，
∴在该空地上种植草皮共需费用为：24×200＝4800（元）．
【点评】本题考查了勾股定理的应用以及勾股定理的逆定理，熟练掌握勾股定理，由勾股定理的逆定理证明△ABC为直角三角形是解题的关键．
24．如图，△ABC的三边分别为AC＝6，BC＝8，AB＝10，如果将△ABC沿AD折叠，使AC恰好落在AB边上．
（1）试判断△ABC的形状，并说明理由．
（2）求线段CD的长．
【分析】（1）根据勾股定理的逆定理，判断AC2+BC2＝62+82＝AB2是否成立即可．
（2）设折叠后点C与AB上的点E重合．在Rt△EBD中，根据勾股定理即可得到一个关于DE的方程，解方程即可求解．
解：（1）△ABC是直角三角形；
理由：∵AC2+BC2＝62+82＝100＝AB2，
∴∠C＝90°；
∴△ABC是直角三角形．
（2）设折叠后点C与AB上的点E重合．
设CD＝x，则DE＝x，AE＝6，BE＝4，BD＝8﹣x；
∵∠AED＝∠C＝90°，
在Rt△EBD中，x2+42＝（8﹣x）2，
解得：x＝3．
即线段CD的长为3．
【点评】本题主要考查了翻折变换（折叠问题），勾股定理的逆定理，以及利用勾股定理把求线段的长的问题转化为方程问题．
25．如图，在直角坐标系中有三点A（﹣2，3）、B（2，1）、C（3，3）．
（1）在平面直角坐标系中画出△ABC；
（2）求△ABC的面积；
（3）P是x轴上的动点，求PA+PB的最小值．
【分析】（1）根据点A，B，C的坐标描点再连线即可．
（2）利用三角形的面积公式计算即可．
（3）取点A关于x轴的对称点A'，连接A'B，交x轴于点P，可得PA+PB最小值即为A'B的长，利用勾股定理计算即可．
解：（1）如图，△ABC即为所求.
（2）△ABC的面积为＝5．
（3）如图，取点A关于x轴的对称点A'，连接A'B，交x轴于点P，连接AP，
此时PA+PB最小，最小值即为A'B的长，
∵＝，
∴PA+PB的最小值为．
【点评】本题考查作图﹣复杂作图、坐标与图形性质、三角形的面积、轴对称﹣最短路线问题，熟练掌握轴对称的性质、勾股定理等知识点是解答本题的关键．
26．如图1，长方形OABC的边OA、OC分别在x轴、y轴上，B点坐标是（8，4），将△AOC沿对角线AC翻折得△ADC，AD与BC相交于点E．
（1）求证：△CDE≌△ABE
（2）求E点坐标；
（3）如图2，动点P从点A出发，沿着折线A→B→C→O运动（到点O停止），是否存在点P，使得△POA的面积等于△ACE的面积，若存在，直接写出点P坐标，若不存在，说明理由．
【分析】（1）用角角边定理即可证明．
（2）设CE＝AE＝n，则BE＝8﹣n，利用勾股定理即可求解．
（3）构建方程确定点P的纵坐标即可解决问题．
解：（1）证明：∵四边形OABC为矩形，
∴AB＝OC，∠B＝∠AOC＝90°，
∴CD＝OC＝AB，∠D＝∠AOC＝∠B，
又∠CED＝∠AEB，
∴△CDE≌△ABE（AAS），
∴CE＝AE；
（2）∵B（8，4），即AB＝4，BC＝8．
∴设CE＝AE＝n，则BE＝8﹣n，
可得（8﹣n）2+42＝n2，
解得：n＝5，
∴E（5，4）；
（3）∵S△ACE＝•CE•AB＝×5×4＝10，
∴S△POA＝•OA•yP＝10，
∴×8×yP＝10，
∴yP＝，
∴满足条件的点P的坐标为（8，）或（0，）．
【点评】本题属于四边形综合题，考查了翻折变换，矩形的性质，三角形的面积等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．