初中数学人教版九年级上册24.4 弧长和扇形面积复习练习题

这是一份初中数学人教版九年级上册24.4 弧长和扇形面积复习练习题，共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
一、单选题
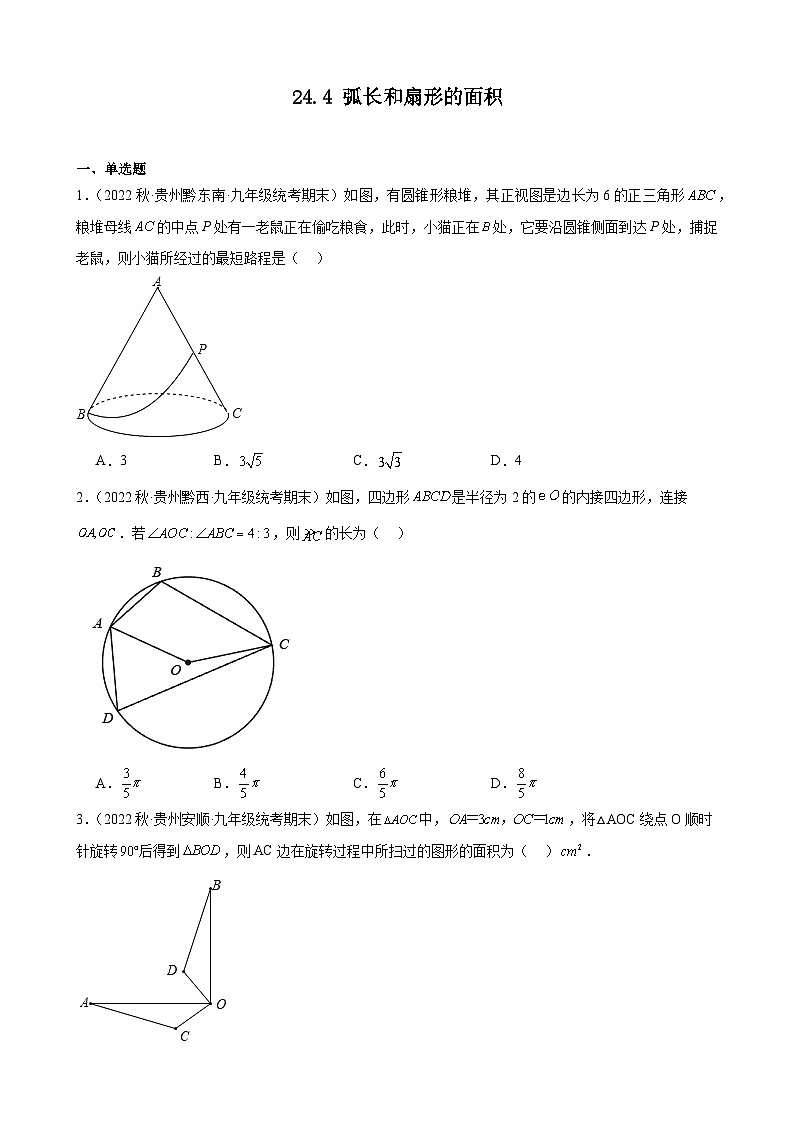
1．（2022秋·贵州黔东南·九年级统考期末）如图，有圆锥形粮堆，其正视图是边长为6的正三角形，粮堆母线的中点P处有一老鼠正在偷吃粮食，此时，小猫正在处，它要沿圆锥侧面到达P处，捕捉老鼠，则小猫所经过的最短路程是（ ）
A．3B．C．D．4
2．（2022秋·贵州黔西·九年级统考期末）如图，四边形是半径为2的的内接四边形，连接．若，则的长为（ ）
A．B．C．D．
3．（2022秋·贵州安顺·九年级统考期末）如图，在中，，将△AOC绕点O顺时针旋转后得到，则AC边在旋转过程中所扫过的图形的面积为（ ）．
A．B．C．D．
4．（2022秋·贵州黔西·九年级统考期末）小明同学在计算某扇形的面积和弧长时，分别写出如下式子：，，经核对，两个结果均正确，则下列说法正确的（ ）
A．该扇形的圆心角为，直径是4B．该扇形的圆心角为，直径是3
C．该扇形的圆心角为，直径是6D．该扇形的圆心角为，直径是4
5．（2022秋·贵州黔东南·九年级期末）如图，半径为10的扇形中，，为弧上一点，，，垂足分别为，．若，则图中阴影部分的面积为（ ）
A．B．C．D．
6．（2022秋·贵州贵阳·九年级期末）如图，在矩形ABCD中，，，以点B为圆心，BC为半径画弧，交AD于点F，则图中阴影部分面积为（ ）．（结果保留）．
A．B．
C．D．
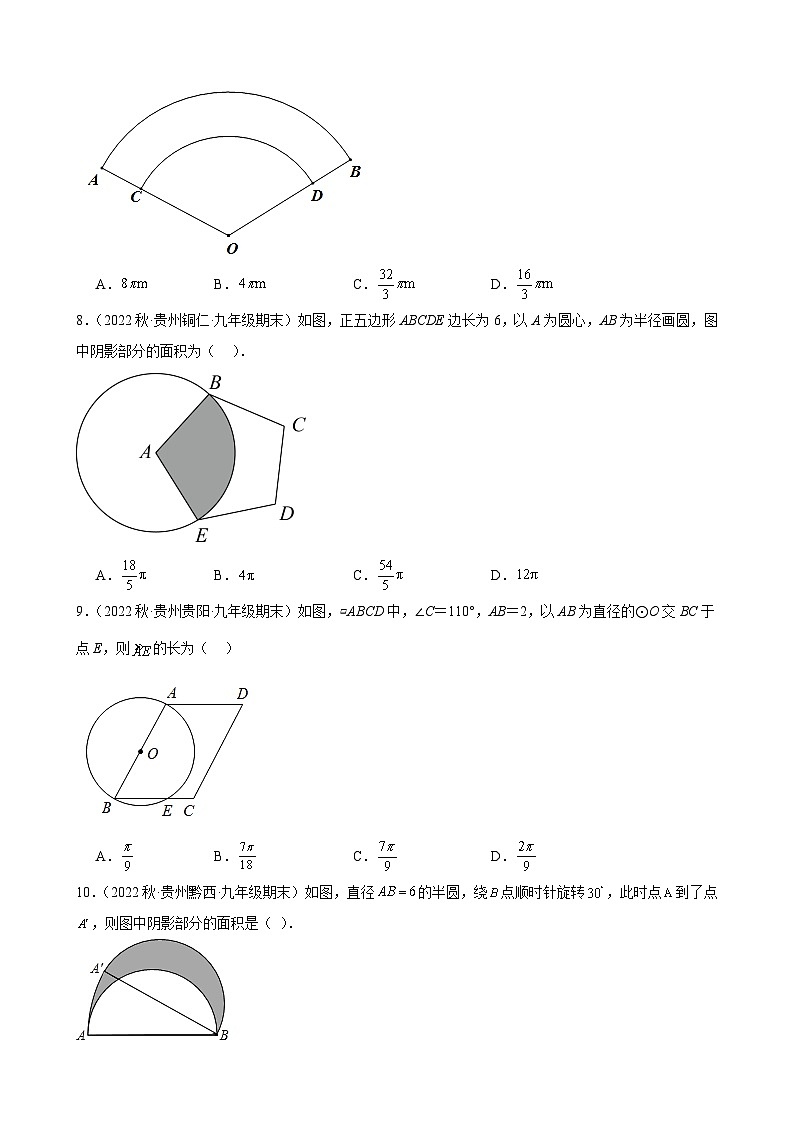
7．（2022秋·贵州安顺·九年级期末）某小区内的消防车道有一段弯道，如图，弯道的内外边缘均为圆弧，，所在圆的圆心为O，点C，D分别在OA，OB上，已知消防车道半径OC=12m，消防车道宽AC=4m，，则弯道外边缘的长为（ ）
A．B．C．D．
8．（2022秋·贵州铜仁·九年级期末）如图，正五边形ABCDE边长为6，以A为圆心，AB为半径画圆，图中阴影部分的面积为（ ）．
A．B．C．D．
9．（2022秋·贵州贵阳·九年级期末）如图，▱ABCD中，∠C＝110°，AB＝2，以AB为直径的⊙O交BC于点E，则的长为（ ）
A．B．C．D．
10．（2022秋·贵州黔西·九年级期末）如图，直径的半圆，绕点顺时针旋转，此时点到了点，则图中阴影部分的面积是（ ）．
A．B．C．D．
11．（2022秋·贵州毕节·九年级期末）在数学跨学科主题活动课上，芳芳用半径，圆心角的扇形纸板，做了一个圆锥形的生日帽，如图所示．在不考虑接缝的情况下，这个圆锥形生日帽的底面圆半径是（ ）
A．B．C．D．
12．（2022秋·贵州铜仁·九年级期末）已知圆锥底面圆的半径为6m，它的侧面积为60πcm2，则这个圆锥的高是（ ）
A．6cmB．8cmC．10cmD．12cm
二、填空题
13．（2022秋·贵州安顺·九年级统考期末）如图，在平面直角坐标系中，点A在y轴的正半轴上，，将绕点O顺时针旋转到，扫过的面积记为，交x轴于点；将绕点O顺时针旋转到，扫过的面积记为，交y轴于点；将绕点O顺时针旋转到，扫过的面积记为，交x轴于点；…；按此规律，则的值为 ．
14．（2022秋·贵州六盘水·九年级统考期末）如图，在边长为10的菱形ABCD中，分别以点A、B、C、D为圆心，以AB为半径画弧，与菱形ABCD的边相交，则图中阴影部分的面积是 ．
15．（2022秋·贵州遵义·九年级统考期末）等腰Rt△A1B1C1，等腰Rt△A2C1C2，等腰Rt△A3C2C3……按如图所示放置，点B的横坐标为1，点A1，A2，A3，A4，……直线y＝x上，分别以A2C2，A3C2，A4C3，……的中点O1，O2，O3……为圆心，A2O1，A3O2，A4O3……的长为半径画弧，，……依次按此作法进行下去，则的长是 （结果保留π）．
16．（2022秋·贵州黔东南·九年级统考期末）如图，是一个半径为6cm，面积为的扇形纸片，现需要一个半径R cm的圆形纸片，使两张纸片刚好能组合成圆锥体，则 cm．
17．（2022秋·贵州黔东南·九年级统考期末）如图，在Rt△ABC中，∠C＝90°，CA＝CB＝2．分别以A、B、C为圆心，以AC为半径画弧，三条弧与边AB所围成的阴影部分的面积是 ．（保留π）
18．（2022秋·贵州黔西·九年级统考期末）如图，从一个边长是5的正五边形纸片上剪出一个扇形（阴影部分），将剪下来的扇形围成一个圆锥，这个圆锥的底面直径为 ．
19．（2022秋·贵州黔西·九年级期末）一个扇形的半径为8cm，弧长为πcm，则扇形的圆心角为 ．
三、解答题
20．（2022秋·贵州遵义·九年级期末）如图，在中，，与，分别相切于点E，F，平分，连接．
（1）求证：是的切线；
（2）若，的半径是1，求图中阴影部分的面积．
21．（2022秋·贵州贵阳·九年级期末）如图，已知，为的直径，过点A作弦垂直于直径于F，点B恰好为 的中点，连接，．
(1)求证：；
(2)若，求的半径；
(3)在（2）的条件下，求阴影部分的面积．
22．（2022秋·贵州铜仁·九年级期末）如图，已知AB是⊙O的直径，点C，D在⊙O上，点E在⊙O外，∠EAC=∠B．
（1）求证：直线AE是⊙O的切线；
（2）若∠D=60°，AB=6时，求劣弧的长（结果保留π）．
参考答案：
1．B
【分析】求这只小猫经过的最短距离的问题首先应转化为圆锥的侧面展开图的问题，转化为平面上两点间的距离的问题．根据圆锥的轴截面是边长为的等边三角形可知，展开图是半径是6的半圆．点是半圆的一个端点，而点是平分半圆的半径的中点，根据勾股定理就可求出两点和在展开图中的距离，就是这只小猫经过的最短距离．
【详解】解：圆锥的底面周长是，则，
，即圆锥侧面展开图的圆心角是180度．
则在圆锥侧面展开图中，，度．
在圆锥侧面展开图中．
故小猫经过的最短距离是．故选：．

【点睛】本题考查的是平面展开最短路线问题，根据题意画出圆锥的侧面展开图，利用勾股定理求解是解答此题的关键．
2．D
【分析】设，则，，利用圆内接四边形的性质得，进而可求得，最后再结合弧长公式进行解答即可．
【详解】解：∵，
∴设，则，
∴，
四边形ABCD内接于，
，
，
解得：，
∴，
又的半径为2，
的长为．
故选：D．
【点睛】本题考查了圆周角定理、圆的内接四边形的性质以及弧长的计算，熟练掌握圆周角定理以及圆的内接四边形的性质是解决本题的关键．
3．B
【分析】根据旋转的性质可以得到阴影部分的面积＝扇形OAB的面积﹣扇形OCD的面积，利用扇形的面积公式即可求解．
【详解】解：
∴阴影部分的面积＝扇形OAB的面积﹣扇形OCD的面积
故选B．
【点睛】考查了旋转的性质以及扇形的面积公式，正确理解：阴影部分的面积＝扇形OAB的面积﹣扇形OCD的面积是解题关键．
4．D
【分析】根据，，可以写出和的形式，然后即可判断哪个选项是正确的，本题得以解决．
【详解】解：，，
，，
该扇形的圆心角为，直径是4，
故选：D．
【点睛】本题考查扇形面积的计算、弧长的计算，解答本题的关键是明确扇形的和．
5．C
【分析】连接OC，易证得四边形CDOE是矩形，则△DOE≌△CEO，得到∠COB＝∠DEO＝40°，图中阴影部分的面积＝扇形OBC的面积，利用扇形的面积公式即可求得．
【详解】解：如图，连接OC，
∵∠AOB＝90°，CD⊥OA，CE⊥OB，
∴四边形CDOE是矩形，
∴OD＝CE，DE＝OC，CD∥OE，
∵∠CDE＝40°，
∴∠DEO＝∠CDE＝40°，
在△DOE和△CEO中，，
∴△DOE≌△CEO（SSS），
∴∠COB＝∠DEO＝40°，
∴图中阴影部分的面积＝扇形OBC的面积，
∵S扇形OBC＝＝，
∴图中阴影部分的面积为，
故选：C．
【点睛】本题考查了扇形面积的计算，矩形的判定与性质，利用扇形OBC的面积等于阴影的面积是解题的关键．
6．A
【分析】连接BE．则阴影部分的面积=S矩形ABCD-S△ABE-S扇形BCE，根据题意知BE=BC=4，则∠AEB=∠EBC=30°，AE=，进而求出即可．
【详解】解：如图，连接BE，
则BE=BC=4，
在Rt△ABE中，AB=2、BE=4，
∴∠AEB=∠EBC=30°，AE=，
则阴影部分的面积=S矩形ABCD-S△ABE-S扇形BCE
=2×4-×2×-
=8--，
故选：A．
【点睛】本题主要考查了扇形面积求法，本题中能够将不规则图形的面积进行转换成规则图形的面积差是解题的关键．
7．C
【分析】确定半径OA，.根据弧长公式可得．
【详解】OA=OC+AC=12+4=16(m)，的长为： （m）,故选C .
【点睛】本题主要考查了弧长的计算公式，解题的关键是牢记弧长的公式．
8．C
【分析】先根据正五边形的内角和求出的度数，再利用扇形的面积公式即可得．
【详解】解：五边形是边长为6的正五边形，
，
则图中阴影部分的面积为，
故选：C．
【点睛】本题考查了扇形的面积、正五边形，熟练掌握正五边形的内角和是解题关键．
9．C
【分析】根据平行线的性质，可以得到∠B的度数，然后根据等腰三角形的性质和三角形的外角与内角的关系，可以得到∠AOB的度数，再根据弧长公式l＝，即可计算出的长．
【详解】解：连接OE，如图：
∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠B+∠C＝180°，
∵∠C＝110°，
∴∠B＝70°，
∵OB＝OE，
∴∠B＝∠OEB，
∴∠OEB＝70°，
∴∠AOE＝∠B+∠OEB＝70°+70°＝140°，
∵AB＝2，AB为⊙O的直径，
∴OA＝OB＝OE＝1，
∴的长为：，
故选：C．
【点睛】本题考查平行四边形的性质、弧长的计算、等腰三角形的性质，解答本题的关键是明确弧长公式和平行四边形的性质，利用数形结合的思想解答．
10．D
【分析】由半圆A′B面积+扇形ABA′的面积-空白处半圆AB的面积即可得出阴影部分的面积．
【详解】解：∵半圆AB，绕B点顺时针旋转30°，
∴S阴影=S半圆A′B+S扇形ABA′-S半圆AB
= S扇形ABA′
=
=3π
故选D．
【点睛】本题考查了扇形面积的计算以及旋转的性质，熟记扇形面积公式和旋转前后不变的边是解题的关键．
11．C
【分析】利用扇形的弧长等于圆锥的底圆周长求解即可．
【详解】解：由题意可知：
扇形的弧长
设底面圆半径为r,
∵扇形的弧长等于圆锥的底圆周长
∴，解得：，
故选：C．
【点睛】本题考查弧长公式，解题的关键是理解扇形的弧长等于圆锥的底圆周长．
12．B
【分析】先根据圆锥的侧面积公式求出圆锥的母线长，然后利用勾股定理求解即可．
【详解】解：设这个圆锥的母线长为lcm，根据题意，得：×2π×6×l＝60π，解得l＝10，
所以圆锥的高＝＝8（cm）．
故选：B．
【点睛】本题考查了圆锥的知识，圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长，掌握基本知识是关键.
13．
【分析】根据等腰直角三角形的性质可得出扇形的半径，写出部分的值，根据数的变化找出变化规律，依此规律即可得出结论．
【详解】由题意、、、、都是等腰直角三角形，
∴，， ，，
∴， ， ， ，；
∴，
∴，
故答案为：
【点睛】本题考查了坐标与图形性质旋转，等腰直角三角形的性质以及扇形的面积，解题的关键是找出规律．
14．25π
【分析】计算四个扇形的面积即可求解．
【详解】解：∵∠ABC+∠BCD+∠CDA+∠DAB=360°，
∴四个扇形的面积，是一个以AB的长为半径的圆，
∴图中阴影部分的面积=π×52=25π，
故答案为：25π．
【点睛】本题考查菱形的性质、扇形面积计算．关键在于图中四个扇形的面积实际上是一个圆的面积．
15．22019π
【分析】根据等腰直角三角形性质，OB＝1，可得A1B＝1，A2C1＝2，A3C2＝4，A4C3＝，可以此类推，则AnCn−1＝2n−1，由分别以A2C1，A3C2，A4C3…的中点O1，O2，O3…为圆心，可得的半径为2−1，的半径为4−2，的半径为8−，可以此类推，的半径为2n−2n−1，再根据是以半径为22021−22020的圆，即可得出答案．
【详解】解：如图所示，根据等腰直角三角形性质可得，
A1B＝1，A2C1＝2，A3C2＝4，A4C3＝，
以此类推，则AnCn−1＝2n−1，
∵的半径为2−1，的半径为4−2，的半径为8−，
以此类推，以此类推，的半径为2n−2n−1，
∴是以半径为22021−22020的圆
∴×2πr＝×2π×(22021−22020)＝π（22020−22019）＝22019π．
故答案为：22019π．
【点睛】本题主要考查了弧长的计算，规律型问题及一次函数图象上坐标的特征，熟练掌握弧长的计算，及一次函数图象上坐标的特征，找出问题的规律进行计算是解决本题的关键．
16．2
【分析】能组合成圆锥体，那么扇形的弧长等于圆形纸片的周长．应先利用扇形的面积=圆锥的弧长母线长，得到圆锥的弧长=2扇形的面积母线长，进而根据圆锥的底面半径=圆锥的弧长求解．
【详解】解：圆锥的弧长,
圆锥的底面半径,
故答案为2．
【点睛】本题考查了求圆锥底面半径，解决本题的难点是得到圆锥的弧长与扇形面积之间的关系，注意利用圆锥的弧长等于底面周长这个知识点．
17．2﹣
【分析】由于三条弧所对的圆心角的和为180°，根据扇形的面积公式可计算出三个扇形的面积和，而三条弧与边AB所围成的阴影部分的面积=S△ABC-三个扇形的面积和，再利用三角形的面积公式计算出S△ABC，然后代入即可得到答案．
【详解】∵在Rt△ABC中，∠C＝90°，CA＝CB＝2．
∴AC =1，S△ABC=×2×2=2，
∵三条弧所对的圆心角的和为180°，
∴三个扇形的面积和==，
∴三条弧与边AB所围成的阴影部分的面积=S△ABC−三个扇形的面积和=2﹣
故答案为：2﹣
【点睛】本题主要考查扇形的面积公式，熟练掌握S扇形=，是解题的关键．
18．3
【分析】先求出正五边形的内角的度数，根据扇形的弧长等于圆锥的底面周长，可求出底面直径．
【详解】解：五边形是正五边形，
，
则弧的长为，即圆锥底面周长为，
圆锥底面直径为，
故答案为：．
【点睛】本题考查正多边形与圆，扇形弧长及圆周长，掌握扇形弧长、圆周长的计算方法是正确解决问题的关键．
19．120°
【详解】试题分析：设扇形的圆心角为n°，
根据题意得π=，解得n=120，
所以扇形的圆心角为120°．
故答案为120°．
考点：弧长的计算．
20．（1）证明见解析；（2）．
【分析】（1）过点作于点，连接，先根据圆的切线的性质可得，再根据角平分线的定义可得，然后根据三角形全等的判定定理与性质可得，最后根据圆的切线的判定即可得证；
（2）设分别交于点，连接，先根据圆的切线的性质、矩形的判定与性质可得，从而可得，再利用勾股定理可得，然后根据直角三角形全等的判定定理与性质可得，从而可得，最后根据图中阴影部分的面积等于即可得．
【详解】证明：（1）如图，过点作于点，连接，
与相切于点，
，
平分，
，
在和中，，
，
，
是的半径，
又，
是的切线；
（2）如图，设分别交于点，连接，
的半径是1，
，
与相切于点，
，
，
四边形是矩形，
，
，
，
，
在和中，，
，
，
，
，
则图中阴影部分的面积为．
【点睛】本题考查了圆的切线的判定与性质、三角形全等的判定定理与性质、扇形的面积公式等知识点，熟练掌握圆的切线的判定与性质是解题关键．
21．(1)证明见详解；
(2)2；
(3)．
【分析】（1）连接 ，，为的直径，得到两个直角及两条线段相等，再根据弧的中点得到弧相等，从而等到角相等，证明两个三角形全等即可得到答案；
（2）连接，根据弧的中点得到弧相等，从而等到圆周角圆心角的关系，结合平角，求出的度数，在中根据勾股定理即可得到答案；
（3）由（2）可得圆心角度数直接求扇形面积，再算出的面积即可得到阴影部分面积．
【详解】（1）证明：连接 ，
∵，为的直径，
∴，，
∵点B是 的中点，
∴，
∴，
在与中，
∵，，，
∴≌，
∴；
（2）解：连接，
∵点B是 的中点，
∴，
∴，，
∵垂直于直径于F， ，
∴，，，
∵，
∴，
∵，
∴，
∴，
∴，
在中，
，
解得：；
（3）由（2）可得，
，
在中，
∴，
∴，，
∴，
∴．
【点睛】本题考查了垂径定理、圆周角定理、扇形的面积以及解直角三角形等，作出辅助线构建直角三角形和等边三角形是解题的关键．
22．（1）证明见试题解析；（2）2π．
【分析】（1）由AB是⊙O的直径，得到∠ACB=90°，∠CBA+∠CAB=90°，由∠EAC=∠B，得到∠CAE+∠BAC=90°，从而可得直线AE是⊙O的切线；
（2）连接CO，计算出AO的长，再利用圆周角定理得到∠AOC的度数，然后利用弧长公式可得答案．
【详解】（1）∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠CBA+∠CAB=90°，
∵∠EAC=∠B，
∴∠CAE+∠BAC=90°，即 BA⊥AE，
∴AE是⊙O的切线；
（2）连接CO，∵AB=6，
∴AO=3，
∵∠D=60°，
∴∠AOC=120°，
∴==2π．