人教B版 (2019)必修 第二册第四章 指数函数、对数函数与幂函数4.6 函数的应用(二)综合训练题

这是一份人教B版 (2019)必修 第二册第四章 指数函数、对数函数与幂函数4.6 函数的应用(二)综合训练题试卷主要包含了6函数的应用，14aB．1，56，31等内容，欢迎下载使用。

一、选择题
1．某研究小组在一项实验中获得一组关于之间的数据，将其整理得到如图所示的散点图，下列函数中最能近似刻画与之间关系的是（ ）
A． B． C． D．
2．某工厂去年总产值为a,计划今后5年内每年比上一年增长10%,则这5年的最后一年该厂的总产值是( )
A．1.14aB．1.15aC．1.16aD．(1+1.15)a
3．我国古代著名的思想家庄子在《庄子·天下篇》中说：“一尺之锤，日取其半，万世不竭”.用现代语言叙述为：一尺长的木棒，每天取其一半，永远也取不完.这样，每天剩下的部分都是前一天的一半，如果把“一尺之锤”看成单位“1”，那么x天后剩下的部分y与x的函数关系式为（ ）
A． B．
C． D．
4．某公司为激励创新，计划逐年加大研发资金投入．若该公司2010年全年投入研发资金130万元，在此基础上，每年投入的研发资金比上一年增长，则该公司全年投入的研发资金开始超过400万元的年份是（参考数据：，，）
A．2018年B．2019年C．2020年D．2021年
5．某创业公司2018年投入的科研资金为100万元，在此基础上，每年投入的科研资金比上一年增长20%，则该厂投入的科研资金开始超过200万元的年份是
A．2021年 B．2022年 C．2023年 D．2024年
6．某储蓄所计划从2004年底起，力争做到每年的吸蓄量比前一年增加8％，则到2007年底该蓄所的吸蓄量比2004年的吸蓄量增加（ ）
A．24% B．32% C．（－1）100％ D．（－1）100％
7．在一定的储存温度范围内，某食品的保鲜时间单位：小时与储存温度单位：满足函数关系为自然对数的底数，k，b为常数，若该食品在时的保鲜时间为120小时，在时的保鲜时间为15小时，则该食品在时的保鲜时间为
A．30小时 B．40小时 C．50小时 D．80小时
8．某化工厂生产一种溶液，按市场要求，杂质含量不能超过0.1%，若初时含杂质2%，每过滤一次可使杂质含量减少，要使产品达到市场要求，则至少应过滤的次数为（已知：lg2=0.3010，lg3=0.4771）（ ）
A．8 B．9 C．10 D．11
9．某工厂2017年投入的科研资金为120万元，在此基础上，每年投入的科研资金比上年增长12%，则该厂投入的科研资金开始超过200万元的年份是（参考数据：lg1.12=0.05，lg3=0.48，lg2=0.30）（ ）
A．2020年 B．2021年 C．2022年 D．2023年
10．双“十一”要到了，某商品原价为元，商家在节前先连续次对该商品进行提价且每次提价.然后在双“十一”期间连续次对该商品进行降价且每次降价.则最后该商品的价格与原来的价格相比
A．相等 B．略有提高 C．略有降低 D．无法确定
11．某公司为激励创新，计划逐年加大研发资金投入，若该公司2017年全年投入研发资金130万元，在此基础上，每年投入的研发资金比上一年增长，则该公司全年投入的研发资金开始超过200万元的年份是（ ）（参考数据：，，）
A．2020年 B．2021年 C．2022年 D．2023年
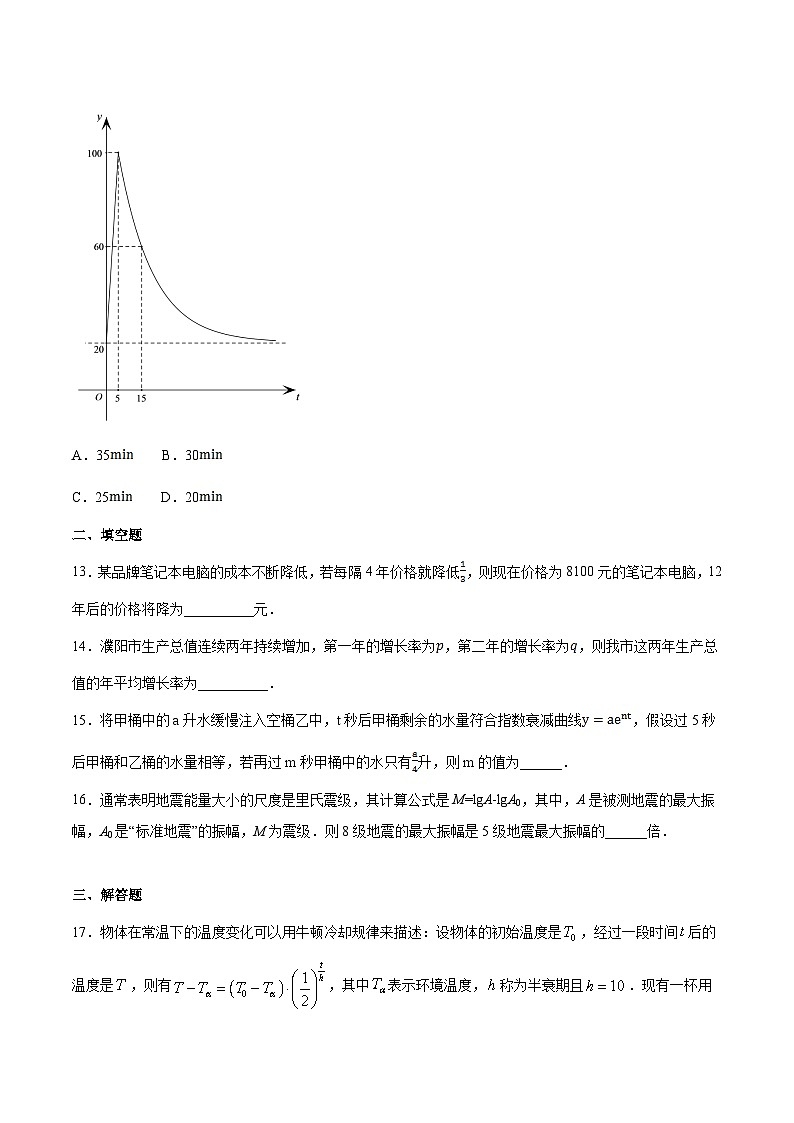
12．某种热饮需用开水冲泡，其基本操作流程如下：①先将水加热到100，水温与时间近似满足一次函数关系；②用开水将热饮冲泡后在室温下放置，温度与时间近似满足函数的关系式为 （为常数）, 通常这种热饮在40时，口感最佳，某天室温为时，冲泡热饮的部分数据如图所示，那么按上述流程冲泡一杯热饮，并在口感最佳时饮用，最少需要的时间为
A．35 B．30
C．25 D．20
二、填空题
13．某品牌笔记本电脑的成本不断降低，若每隔4年价格就降低，则现在价格为8100元的笔记本电脑，12年后的价格将降为__________元．
14．濮阳市生产总值连续两年持续增加，第一年的增长率为，第二年的增长率为，则我市这两年生产总值的年平均增长率为__________．
15．将甲桶中的a升水缓慢注入空桶乙中，t秒后甲桶剩余的水量符合指数衰减曲线，假设过5秒后甲桶和乙桶的水量相等，若再过m秒甲桶中的水只有升，则m的值为______．
16．通常表明地震能量大小的尺度是里氏震级，其计算公式是M=lgA-lgA0，其中，A是被测地震的最大振幅，A0是“标准地震”的振幅，M为震级．则8级地震的最大振幅是5级地震最大振幅的______倍．
三、解答题
17．物体在常温下的温度变化可以用牛顿冷却规律来描述：设物体的初始温度是，经过一段时间后的温度是，则有，其中表示环境温度，称为半衰期且．现有一杯用热水冲的速溶咖啡，放置在的房间中分钟，求此时咖啡的温度是多少度？如果要降温到，共需要多长时间？（，结果精确到）
18．某种放射性元素的原子数随时间的变化规律是，其中是正的常数， 为自然对数的底数.
（1）判断函数是增函数还是减函数；
（2）把表示成原子数的函数.
19．数据显示，某公司2018年上半年五个月的收入情况如下表所示：
根据上述数据，在建立该公司2018年月收入（万元）与月份的函数模型时，给出两个函数模型与供选择.
（1）你认为哪个函数模型较好，并简单说明理由；
（2）试用你认为较好的函数模型，分析大约从第几个月份开始，该公司的月收入会超过100万元？（参考数据，）
20．大西洋鲑鱼每年都要逆流而上，游回产地产卵，经研究发现鲑鱼的游速可以表示为函数y=lg3（），单位是m/s，θ是表示鱼的耗氧量的单位数．
（1）当一条鲑鱼的耗氧量是900个单位时，它的游速是多少？
（2）计算一条鱼静止时耗氧量的单位数.
（3）某条鲑鱼想把游速提高1 m/s，那么它的耗氧量的单位数是原来的多少倍？
21．科学研究表明：人类对声音有不的感觉，这与声音的强度单位：瓦平方米有关在实际测量时，常用单位：分贝来表示声音强弱的等级，它与声音的强度I满足关系式：是常数，其中瓦平方米如风吹落叶沙沙声的强度瓦平方米，它的强弱等级分贝．
已知生活中几种声音的强度如表：
声音来源
求a和m的值
为了不影响正常的休息和睡眠，声音的强弱等级一般不能超过50分贝，求此时声音强度I的最大值．
22．医药公司针对某种疾病开发了一种新型药物，患者单次服用制定规格的该药物后，其体内的药物浓度随时间的变化情况（如图所示）：当时，与的函数关系式为（为常数）；当时，与的函数关系式为（为常数）.服药后，患者体内的药物浓度为，这种药物在患者体内的药物浓度不低于最低有效浓度，才有疗效；而超过最低中毒浓度，患者就会有危险.
（1）首次服药后，药物有疗效的时间是多长？
（2）首次服药1小时后，可否立即再次服用同种规格的这种药物?
（参考数据：，）
第四章 指数函数、对数函数与幂函数
4.6函数的应用（二）
一、选择题
1．某研究小组在一项实验中获得一组关于之间的数据，将其整理得到如图所示的散点图，下列函数中最能近似刻画与之间关系的是（ ）

A． B． C． D．
【答案】C
【解析】
根据图中的特殊点（2,1），（4,2）,通过选项可知只有C：满足题意.故选C.
2．某工厂去年总产值为a,计划今后5年内每年比上一年增长10%,则这5年的最后一年该厂的总产值是( )
A．1.14aB．1.15aC．1.16aD．(1+1.15)a
【答案】B
【解析】
由题意,得x年后的总产值为y=a·(1+10%)x,
则5年后的总产值为a(1+10%)5,即1.15a.
本题选择B选项.
3．我国古代著名的思想家庄子在《庄子·天下篇》中说：“一尺之锤，日取其半，万世不竭”.用现代语言叙述为：一尺长的木棒，每天取其一半，永远也取不完.这样，每天剩下的部分都是前一天的一半，如果把“一尺之锤”看成单位“1”，那么x天后剩下的部分y与x的函数关系式为（ ）
A． B．
C． D．
【答案】D
【解析】
由题意可得：剩下的部分所构成的数列为，
∴x天后剩下的部分y与x的函数关系式为
故选：D
4．某公司为激励创新，计划逐年加大研发资金投入．若该公司2010年全年投入研发资金130万元，在此基础上，每年投入的研发资金比上一年增长，则该公司全年投入的研发资金开始超过400万元的年份是（参考数据：，，）
A．2018年B．2019年C．2020年D．2021年
【答案】C
【解析】
根据题意，设第年开始超过400万元，
则，
化为：，
解可得：；
则，
故选：C．
5．某创业公司2018年投入的科研资金为100万元，在此基础上，每年投入的科研资金比上一年增长20%，则该厂投入的科研资金开始超过200万元的年份是
A．2021年 B．2022年 C．2023年 D．2024年
【答案】B
【解析】
某创业公司2018年投入的科研资金为100万元，
在此基础上，每年投入的科研资金比上一年增长20%，
则x年后投入的科研资金为：
y＝100（1+20%）x＝100×1.2x，
由100×1.2x＞200，
解得x≥4．
该厂投入的科研资金开始超过200万元的年份是2018+4＝2022年．
故选：B．
6．某储蓄所计划从2004年底起，力争做到每年的吸蓄量比前一年增加8％，则到2007年底该蓄所的吸蓄量比2004年的吸蓄量增加（ ）
A．24% B．32% C．（－1）100％ D．（－1）100％
【答案】C
【解析】
设2004年储蓄量为 ，根据等比数列通项公式得
2005年储蓄量为
2006年储蓄量为
2007年储蓄量为
所以2007年底该蓄所的吸蓄量比2004年的吸蓄量增加了

所以选C
7．在一定的储存温度范围内，某食品的保鲜时间单位：小时与储存温度单位：满足函数关系为自然对数的底数，k，b为常数，若该食品在时的保鲜时间为120小时，在时的保鲜时间为15小时，则该食品在时的保鲜时间为
A．30小时 B．40小时 C．50小时 D．80小时
【答案】A
【解析】
由题意可知，，，
．
故选：A．
8．某化工厂生产一种溶液，按市场要求，杂质含量不能超过0.1%，若初时含杂质2%，每过滤一次可使杂质含量减少，要使产品达到市场要求，则至少应过滤的次数为（已知：lg2=0.3010，lg3=0.4771）（ ）
A．8 B．9 C．10 D．11
【答案】D
【解析】
设至少需要过滤次，则，
即,
所以，
即，
又，所以，
所以至少过滤11次才能使产品达到市场要求,故选D．
9．某工厂2017年投入的科研资金为120万元，在此基础上，每年投入的科研资金比上年增长12%，则该厂投入的科研资金开始超过200万元的年份是（参考数据：lg1.12=0.05，lg3=0.48，lg2=0.30）（ ）
A．2020年 B．2021年 C．2022年 D．2023年
【答案】C
【解析】
设第n年后，建立不等式，

故从2017年起第5年，故为2022，故选C.
10．双“十一”要到了，某商品原价为元，商家在节前先连续次对该商品进行提价且每次提价.然后在双“十一”期间连续次对该商品进行降价且每次降价.则最后该商品的价格与原来的价格相比
A．相等 B．略有提高 C．略有降低 D．无法确定
【答案】C
【解析】
==<1，
故选C.
11．某公司为激励创新，计划逐年加大研发资金投入，若该公司2017年全年投入研发资金130万元，在此基础上，每年投入的研发资金比上一年增长，则该公司全年投入的研发资金开始超过200万元的年份是（ ）（参考数据：，，）
A．2020年 B．2021年 C．2022年 D．2023年
【答案】B
【解析】
由题意求满足最小n值，
由得

，开始超过200万元的年份是2017+5-1=2021,选B.
12．某种热饮需用开水冲泡，其基本操作流程如下：①先将水加热到100，水温与时间近似满足一次函数关系；②用开水将热饮冲泡后在室温下放置，温度与时间近似满足函数的关系式为 （为常数）, 通常这种热饮在40时，口感最佳，某天室温为时，冲泡热饮的部分数据如图所示，那么按上述流程冲泡一杯热饮，并在口感最佳时饮用，最少需要的时间为

A．35 B．30
C．25 D．20
【答案】C
【解析】
由题意，当0≤t≤5时，函数图象是一个线段，当t≥5时，函数的解析式为，
点（5，100）和点（15，60），代入解析式，
有，
解得a＝5,b=20，
故函数的解析式为，t≥5．令y=40，解得t=25,
∴最少需要的时间为25min．
故选C.
二、填空题
13．某品牌笔记本电脑的成本不断降低，若每隔4年价格就降低，则现在价格为8100元的笔记本电脑，12年后的价格将降为__________元．
【答案】2400
【解析】
12年后的价格可降为81002400元．
故答案为2400．
14．濮阳市生产总值连续两年持续增加，第一年的增长率为，第二年的增长率为，则我市这两年生产总值的年平均增长率为__________．
【答案】
【解析】
设该市这两年生产总值的年平均增长率为,由题意,
所以，故填.
15．将甲桶中的a升水缓慢注入空桶乙中，t秒后甲桶剩余的水量符合指数衰减曲线，假设过5秒后甲桶和乙桶的水量相等，若再过m秒甲桶中的水只有升，则m的值为______．
【答案】5
【解析】
秒后两桶水量相等
若秒后水量为： ，即

本题正确结果：
16．通常表明地震能量大小的尺度是里氏震级，其计算公式是M=lgA-lgA0，其中，A是被测地震的最大振幅，A0是“标准地震”的振幅，M为震级．则8级地震的最大振幅是5级地震最大振幅的______倍．
【答案】
【解析】
由M=lgA-lgA0可得，M=， A=•．
当M=8时，地震的最大振幅为=•108；
当M=5时，地震的最大振幅为=•105；
∴两次地震的最大振幅之比是：，
∴8级地震的最大振幅是5级地震的最大振幅的1000倍．
故答案为：1000．
三、解答题
17．物体在常温下的温度变化可以用牛顿冷却规律来描述：设物体的初始温度是，经过一段时间后的温度是，则有，其中表示环境温度，称为半衰期且．现有一杯用热水冲的速溶咖啡，放置在的房间中分钟，求此时咖啡的温度是多少度？如果要降温到，共需要多长时间？（，结果精确到）
【答案】，需要约分钟．
【解析】
由条件知，，，．
代入，得，
解得；
如果要降温到，则．
解得．
答：此时咖啡的温度，要降温到，共需要约分钟．
18．某种放射性元素的原子数随时间的变化规律是，其中是正的常数， 为自然对数的底数.
（1）判断函数是增函数还是减函数；
（2）把表示成原子数的函数.
【答案】(1)减函数；(2) （其中）.
【解析】
（1）由已知可得
因为是正常数， ，所以，即，
又是正常数，所以是关于的减函数
（2）因为，所以，所以，即（其中）.
19．数据显示，某公司2018年上半年五个月的收入情况如下表所示：
根据上述数据，在建立该公司2018年月收入（万元）与月份的函数模型时，给出两个函数模型与供选择.
（1）你认为哪个函数模型较好，并简单说明理由；
（2）试用你认为较好的函数模型，分析大约从第几个月份开始，该公司的月收入会超过100万元？（参考数据，）
【答案】（1）函数这一模型较好（2）大约从第9月份开始
【解析】
（1）画出散点图

由图可知点 基本上是落在函数的图像的附近，
因此用函数这一模型较好
（2）当时， ，
即
故大约从第9月份开始，该公司的月收入会超过100万元.
另解：当时，

故大约从第9月份开始，该公司的月收入会超过100万元.
20．大西洋鲑鱼每年都要逆流而上，游回产地产卵，经研究发现鲑鱼的游速可以表示为函数y=lg3（），单位是m/s，θ是表示鱼的耗氧量的单位数．
（1）当一条鲑鱼的耗氧量是900个单位时，它的游速是多少？
（2）计算一条鱼静止时耗氧量的单位数.
（3）某条鲑鱼想把游速提高1 m/s，那么它的耗氧量的单位数是原来的多少倍？
【答案】（1）1（2）100(3)9
【解析】
(1)由y=lg3（）可知，
当θ＝900时，v＝lg3＝lg39＝1(m/s)．
所以当一条鲑鱼的耗氧量是900个单位时，它的游速是1 m/s.
（2)令y=0，则

(3)由v2－v1＝1，即lg3－lg3＝1，得＝9.
所以耗氧量的单位数为原来的9倍．
21．科学研究表明：人类对声音有不的感觉，这与声音的强度单位：瓦平方米有关在实际测量时，常用单位：分贝来表示声音强弱的等级，它与声音的强度I满足关系式：是常数，其中瓦平方米如风吹落叶沙沙声的强度瓦平方米，它的强弱等级分贝．
已知生活中几种声音的强度如表：
声音来源
求a和m的值
为了不影响正常的休息和睡眠，声音的强弱等级一般不能超过50分贝，求此时声音强度I的最大值．
【答案】（1），；（2）瓦平方米
【解析】
（1）将瓦平方米，瓦平方米代入
得：
则：
由题意得：，即：，
得，即
此时声音强度的最大值为瓦平方米
22．医药公司针对某种疾病开发了一种新型药物，患者单次服用制定规格的该药物后，其体内的药物浓度随时间的变化情况（如图所示）：当时，与的函数关系式为（为常数）；当时，与的函数关系式为（为常数）.服药后，患者体内的药物浓度为，这种药物在患者体内的药物浓度不低于最低有效浓度，才有疗效；而超过最低中毒浓度，患者就会有危险.
（1）首次服药后，药物有疗效的时间是多长？
（2）首次服药1小时后，可否立即再次服用同种规格的这种药物?
（参考数据：，）

【答案】（1）小时；（2）见解析
【解析】
（1）当时，，函数图像过点，
所以，得
所以当时，
当时，，函数图像过点
所以，所以
由，得，所以
则药物有疗效时间为小时.
（2）设再次服用同等规格的药物小时后的药物浓度为
当时，
因为函数在内单调递增，
所以当时，
当时，
因为，所以首次服药后1小时，可以立即再次服用同等规格的药物.

月份
2
3
4
5
6
月收入（万元）
1.4
2.56
5.31
11
21.3
声音大小
风吹落叶沙沙声
轻声耳语
很嘈杂的马路
强度瓦平方米
强弱等级分贝
10
m
90
月份
2
3
4
5
6
月收入（万元）
1.4
2.56
5.31
11
21.3
声音大小
风吹落叶沙沙声
轻声耳语
很嘈杂的马路
强度瓦平方米
强弱等级分贝
10
m
90