河南省安阳市五中学区2023-2024学年九年级上学期10月学情调研数学试题

这是一份河南省安阳市五中学区2023-2024学年九年级上学期10月学情调研数学试题，共3页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
2．若关于的一元二次方程的一个根是1，则的值是（ ）
A．B．1C．1或D．或0
3．关于二次函数，下列说法正确的是（ ）
A．函数图象的开口向下B．函数图象的顶点坐标为
C．该函数有最大值，最大值为5D．当时，随的增大而增大
4．如图，在中，，将绕点逆时针旋转到的位置，使得，划的度数是（ ）
A．35°B．40°C．50°D．70°
5．已知、、是二次函数图象上的三点，则、、的大小关系为（ ）
A．B．C．D．
6．二次函数的图象与轴有两个不同交点，则可以是（ ）
A．0B．1C．2D．3
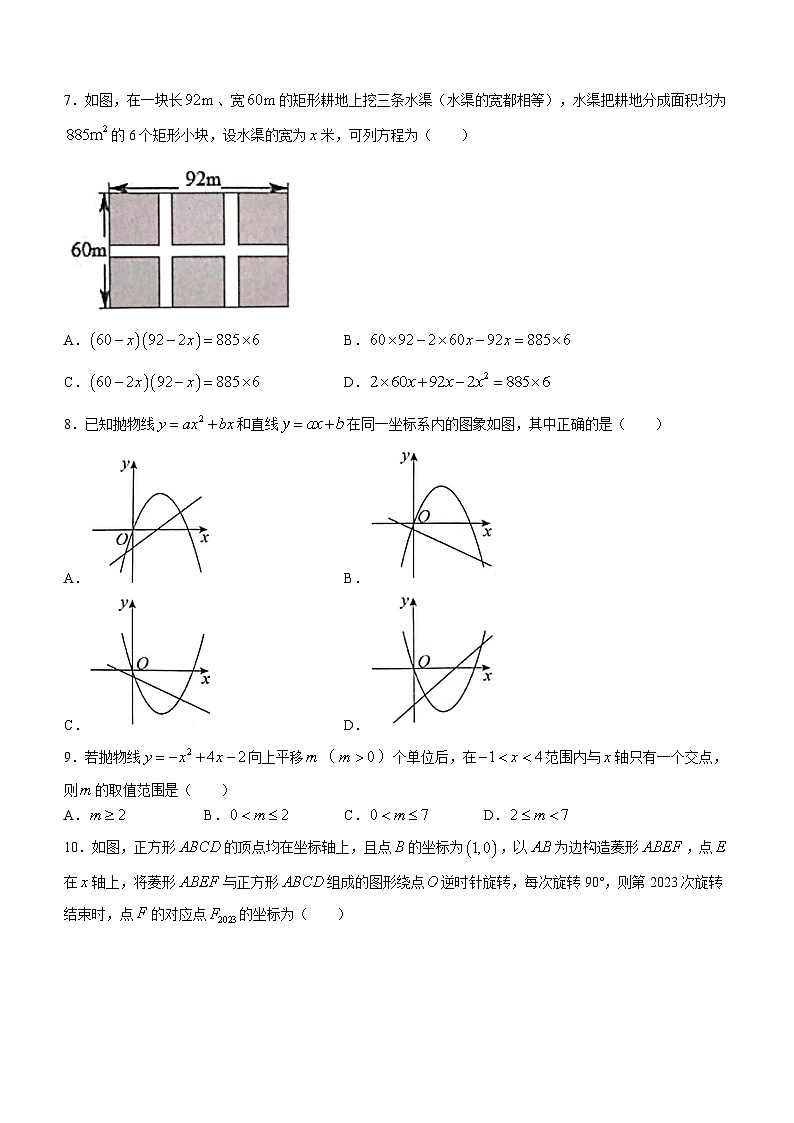
7．如图，在一块长、宽的矩形耕地上挖三条水渠（水渠的宽都相等），水渠把耕地分成面积均为的6个矩形小块，设水渠的宽为米，可列方程为（ ）
A．B．
C．D．
8．已知抛物线和直线在同一坐标系内的图象如图，其中正确的是（ ）
A．B．
C．D．
9．若抛物线向上平移（）个单位后，在范围内与轴只有一个交点，则的取值范围是（ ）
A．B．C．D．
10．如图，正方形的顶点均在坐标轴上，且点的坐标为，以为边构造菱形，点在轴上，将菱形与正方形组成的图形绕点逆时针旋转，每次旋转90°，则第2023次旋转结束时，点的对应点的坐标为（ ）
第10题图
A．B．C．D．
二、填空题（共15分）
11．方程的根是______．
12．设，是方程的两个不相等的实数根，则的值为______．
13．在平面直角坐标系中，已知点和点关于原点对称，则______．
14．将抛物线先向右平移1个单位长度，再向上平移2个单位长度，得到的抛物线的函数表达式为，则的值为______．
15．如图，等腰中，是上一动点，连接．将绕点逆时针旋转90°得到，连接．若，则周长最小值是______．
第15题图
三、解答题（共75分）
16．（本题8分）解下列方程：
（1）；
（2）．
17．（本题9分）已知：关于的方程．
（1）不解方程，判别方程根的情况，并说明理由；
（2）若，是该方程的两个实数根，且，求的值．
18．（本题9分）如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，的顶点均在格点上．
（1）画出将关于原点的中心对称图形；
（2）将绕点顺时针旋转90°得到，画出；
（3）若由绕着某点旋转得到的，则这点的坐标为______．
19．（本题9分）2022年北京冬季奥运会于2月4日至2月20日在北京市和河北省张家口市联合举行，冬奥会吉祥物为“冰墩墩”。
（1）据市场调研发现，某工厂今年二月份共生产500个“冰墩墩”，该工厂连续两个月增加生产量后四月份生产720个“冰墩墩”，求平均每月的增长率是多少？
（2）已知某商店“冰墩墩”平均每天可销售20个，每个盈利20元，在每个降价幅度不超过8元的情况下，每下降2元，则每天可多售10件．如果每天要盈利700元，则每个“冰墩墩”应降价多少元？
20．（本题9分）课本知识再现：
（Ⅰ）归纳（八年级上册课本70页）：点关于轴对称的点的坐标为；点关于轴对称的点的坐标为；
（Ⅱ）归纳（九年级上册课本68页）：两个点关于原点对称时，它们的坐标符号相反，即点关于原点的对称点为．
小颖在学习完《旋转》与《二次函数》两章后，从点的对称角度思考函数图象的对称，发现一次函数、二次函数图象上也可以应用点的对称特点．
（1）根据上面知识，求与已知直线关于轴对称的直线的解析式；
解：∵点关于轴对称的点的坐标为；
即直线上的点关于轴对称的直线上的点为，
∴．
∴与已知直线关于轴对称的直线的解析式为．
理解上面的解题过程，并完成填空：
与已知直线关于轴对称的直线的解析式为______；
（2）已知二次函数的图象与抛物线关于原点对称，求，，的值；
（3）判断以下每对函数的图象：①与；②与；③与；④与．其中一定关于原点对称的是______（填序号）．
21．（本题10分）如图，在某中学的一场篮球赛中，李明在距离篮圈中心（水平距离）处跳起投篮，球出手时离地面，当篮球运行的水平距离为时达到离地面的最大高度．已知篮球在空中的运行路线为一条抛物线，篮圈中心距地面．
（1）建立如图所示的平面直角坐标系，求篮球运动路线所在抛物线的函数解析式；
（2）场边看球的小丽认为，李明投出的此球不能命中篮圈中心．请通过计算说明小丽判断的正确性；
（3）在球出手后，未达到最高点时，被防守队员拦截下来称为盖帽．但球到达最高点后，处于下落过程时，防守队员再出手拦截，属于犯规．在（1）的条件下，防守方球员张亮前来盖帽，已知张亮的最大摸球高度为，则他应该在李明前面多少米范围内跳起拦截才能盖帽成功？
22．（本题10分）如图，二次函数的图象与轴交于点和点，与轴交于点．
（1）求二次函数的解析式；
（2）求点坐标，并结合图象写出时，的取值范围；
（3）直线交抛物线于点，，若点在抛物线上且位于直线的上方（不与，重合），直接写出点的纵坐标的取值范围．
23．（本题11分）已知四边形和都为正方形，连接，，，点，，分别是，，的中点．
图① 图② 图③
（1）观察思考
如图①，点，分别在，上，线段和的数量关系和位置关系为______；
（2）探究证明
如图②，将正方形绕点旋转，在旋转的过程中和的上述关系是否发生变化？请结合图②说明理由；
（3）综合实践
如图③，连接，取的中点，连接，．
①判断四边形的形状，并说明理由；
②若，，在旋转的过程中，四边形的周长的最大值为______．
数学参考答案
1．C
【详解】解：选项，不是轴对称图形，故选项，不符合题意；
选项，不是轴对称图形，故选项，不符合题意；
选项，既是轴对称图形又是中心对称图形，故选项，符合题意；
选项，不是中心对称图形，故选项，不符合题意；
故选：．
2．A
【详解】解：把代入方程得：，即，
开方得：或，
∵，即，
∴．
故选：A．
3．D
【详解】解：中，
的系数为1，，函数图象开口向上，A错误；
函数图象的顶点坐标是，B错误；
函数图象开口向上，有最小值为5，C错误；
函数图象的对称轴为，时y随x的增大而减小；时，y随x的增大而增大，所以，当时，y随x的增大而增大，故D正确．
故选：D．
4．B
【详解】解：∵，
∴，
∵将绕点逆时针旋转到的位置，
∴，
∴，
∴，
，，
∴，即旋转角的度数是，
故选：B．
5．A
【详解】解：二次函数的关系式为，
∴抛物线开口向上，对称轴为直线，距离对称轴越近，函数值越小，
∵，，，
∴
∴，
故选：A．
6．B
【详解】∵二次函数的图像与x轴有两个不同的交点，
∴，，
解得，且，
所以a可以是1．
故选：B．
7．A
【详解】在一块长92m、宽60m的矩形耕地上挖三条水渠（水渠的宽都相等），水渠把耕地分成面积均为的6个矩形小块，设水渠的宽为x米，可列方程为
故选：A
8．D
【详解】解：A．由二次函数图象的开口方向可知，根据对称轴在y轴的右侧，可知a、b异号，，此时直线应经过一、二、四象限，与图中一次函数图象不一致，故可排除；
B．由二次函数图象的开口方向可知，根据对称轴在y轴的右侧，可知a、b异号，，此时直线应经过一、二、四象限，与图中一次函数图象不一致，故可排除；
C．由二次函数图象的开口方向可知，根据对称轴在y轴的右侧，可知a、b异号，，此时直线应经过一、三、四象限，与图中一次函数图象不一致，故可排除；
D．由二次函数图象的开口方向可知，根据对称轴在y轴的右侧，可知a、b异号，，此时直线应经过一、三、四象限，与图中一次函数图象一致，符合要求；
故选D．
D
【详解】解：根据题意，平移后的抛物线的表达式为，
∵平移后抛物线的开口向下，对称轴为直线，
∴要使在范围内与x轴只有一个交点，只需时对应图象上的点在x轴下方，时对应函数图象上的点在x轴上或x轴上方，如图，

∴，解得，
故选：D．
10．B
【详解】解：由题意知，，
由勾股定理得，，
∵菱形，
∴，
∴，
∵每次旋转，
∴每旋转4次，点F重合一次，
∵，
∴，
∵在第四象限，如图，连接，，作于，

由旋转的性质可得，，，
∵，
∴，
∵，，，
∴，
∴，，
∴，
∴，
故选：B．
11.
【详解】解：，
∴，
即，
∴或，
解得：，
故答案为：．
12．2022
【详解】解：a，b是方程的两个不相等的实数根，
、，
．
故答案为：2022．
13．1
【详解】解：∵点和点关于原点对称，
∴，
∴，
故答案为：1．
14．
【详解】将抛物线先向右平移1个单位长度，再向上平移2个单位长度后得到的抛物线对应的函数表达式为：，
∴，
解得．
故答案为：．
15．
【详解】解：∵为等腰直角三角形，，
∴，，
∵将绕点逆时针旋转得到，
∴，
∴，是等腰直角三角形，
∴，
∴当取最小值时，的值最小，则周长的值最小，
当时，的值最小，
∵是等腰直角三角形，，
∴，
∴的值最小时，可有，
∴，
∴周长最小值是．
故答案为：．
16．(1)
(2)，
【详解】（1）解：∵，
∴，
∴或，
解得；（4分）
（2）解：，
，
，
，
，
∴，
∴，．（8分）
17．(1)方程有两个不相等的实数根，理由见解析；
(2)，．
【详解】（1）依题意得：．
方程有两个不相等的实数根．（4分）
（2）由一元二次方程的根与系数的关系可得：，
．
，
解得，．（9分）
18．(1)见解析
(2)见解析
(3)
【详解】（1）解：如图，即为所求；（3分）
；
（2）解：如图，即为所求；（6分）
（3）解：根据旋转的性质可得，旋转中心为和垂直平分线的交点，图中点P即为旋转中心，
∴，(9分)
故答案为：．
19．(1)
(2)6元
【详解】（1）解：设平均每月的增长率是，
（个），
解得，（舍）
答：平均每月的增长率是．（4分）
（2）设每个“冰墩墩”降价元，则每个盈利元，平均每天可售出个，
依题意得：，
整理得：，
解得：（不符合题意，舍去）
答：每个“冰墩墩”应降价6元．（9分）
20.解:(1)y=-2x-3(3分)
(2)∵P(x，y)关于原点的对称点为P'(-x，-y),即抛物线 y=-2x2+8x-7上的点(x,y)关于原点对称的抛物线上的点为(-x，-y),∴-y=-2(-x)²+8(-x)-7=-2x²-8x-7,即y=2x²+8x+7∴二次函数y=ax2+bx+c中的 a=2,b=8，c=7(6分)(3)③(9分)
21．(1)
(2)小丽的判断是正确的，计算过程见解析
(3)张亮应在李明前面1米范围内处跳起拦截才能盖帽成功
【详解】（1）抛物线顶点坐标为，
设抛物线的解析式为．
把代入，得．
；（3分）
（2）把代入抛物线解析式
得．
，
此球不能投中，小丽的判断是正确的．（6分）
（3）当时，，
解之，得或．
，．
答：张亮应在李明前面1米范围内处跳起拦截才能盖帽成功．（10分）
22．(1)
(2)，或
(3) -5＜yp ≤4 或
【详解】（1）解：∵二次函数的图象经过点，，
∴，
解得，
∴该二次函数的解析式为．（3分）
（2）解：由（1）可知，二次函数的解析式为，
当=0时，，
解得，
∴．
根据图象可知，当时，的取值范围为或．（6分）
（3）解：∵，
∴当时，y取得最大值，最大值为4，
当时，，
当时，，
解得：或2，
∴点，或，
∵点P在抛物线上且位于直线l的上方（不与M，N重合），
当点时，；
当时，；
综上所述，点P的纵坐标yp的取值范围(3) -5＜yp ≤4 或（10分）
23．(1)且
(2)不变，理由见解析
(3)①四边形是正方形，理由见解析；②16
【详解】（1）解：∵四边形和都为正方形，
∴，，，
∴，，
∵，，分别为，，的中点，
∴且，且，
∴且；
故答案为：且；（2分）
（2）且，理由如下：
∵，，分别为，，的中点，
∴且，且，
由旋转知，，
，，
∴，
∴，，
∴
，
∴与的夹角为，
∴
∴且；（6分）
（3）①四边形是正方形，理由如下：
∵，分别为，的中点
∴，，
由（2）知，，，
∴，，
∴四边形是平行四边形
∵，且，
∴是正方形；（9分）
②当点在线段上时，长最大，
此时，,
∴，
∴四边形的周长的最大值为，．
故答案为：16．（11分）