




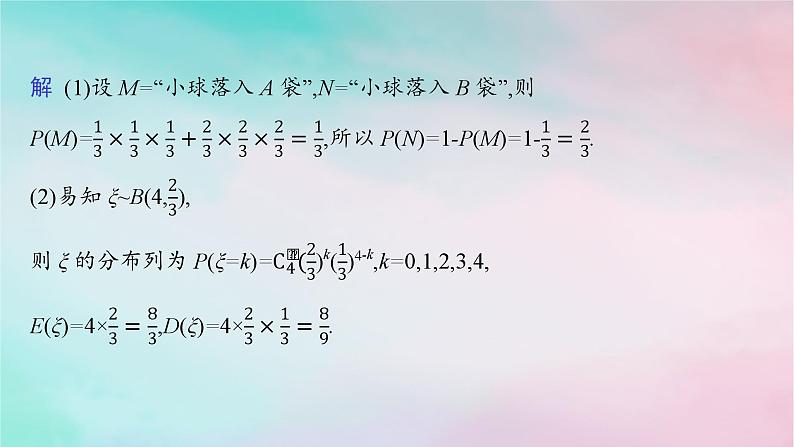


还剩24页未读,
继续阅读
成套系列资料,整套一键下载
- 新教材2023_2024学年高中数学第7章随机变量及其分布7.4二项分布与超几何分布7.4.2超几何分布课件新人教A版选择性必修第三册 课件 0 次下载
- 新教材2023_2024学年高中数学第7章随机变量及其分布7.5正态分布课件新人教A版选择性必修第三册 课件 0 次下载
- 新教材2023_2024学年高中数学第7章随机变量及其分布本章总结提升课件新人教A版选择性必修第三册 课件 0 次下载
- 新教材2023_2024学年高中数学第8章成对数据的统计分析8.1成对数据的统计相关性8.1.1变量的相关关系8.1.2样本相关系数课件新人教A版选择性必修第三册 课件 0 次下载
- 新教材2023_2024学年高中数学第8章成对数据的统计分析8.2一元线性回归模型及其应用8.2.1一元线性回归模型8.2.2一元线性回归模型参数的最玄乘估计课件新人教A版选择性必修第三册 课件 0 次下载
新教材2023_2024学年高中数学第7章随机变量及其分布培优课__离散型随机变量的均值与方差的综合应用课件新人教A版选择性必修第三册
展开
这是一份新教材2023_2024学年高中数学第7章随机变量及其分布培优课__离散型随机变量的均值与方差的综合应用课件新人教A版选择性必修第三册,共32页。
第七章培优课——离散型随机变量的均值与方差的综合应用重难探究·能力素养全提升成果验收·课堂达标检测目录索引 重难探究·能力素养全提升探究点一 二项分布均值与方差的综合【例1】 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,在下落的过程中,每次遇到障碍物时,小球向左、右两边下落的概率分别是 ,小球最后落入A袋或B袋中.(1)分别求出小球落入A袋和B袋中的概率;(2)在容器的入口处依次放入4个小球,记ξ为落入B袋中的小球的个数,求ξ的分布列、均值和方差.规律方法 通过审题,明确判断出随机变量X(击中次数)服从二项分布是解题的关键,然后利用二项分布的均值和方差的计算公式即可求出E(X),D(X).变式训练1某运动员投篮命中率P=0.6.(1)求1次投篮命中次数ξ的均值与方差;(2)求重复5次投篮时,命中次数η的均值与方差.解 (1)投篮1次只有两种结果,投篮命中ξ=1,不中ξ=0,服从两点分布,其分布列为则E(ξ)=1×0.6=0.6,D(ξ)=(1-0.6)×0.6=0.24.(2)由题意,重复5次投篮,命中的次数η服从二项分布,即η~B(5,0.6).由二项分布均值与方差的计算公式知,E(η)=5×0.6=3,D(η)=5×0.6×0.4=1.2.探究点二 离散型随机变量的均值与方差的常见类型【例2】 设袋子中装有a个红球、b个黄球、c个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.(1)当a=3,b=2,c=1时,从该袋子中任取一个球,记下颜色后放回,再取一个球(每球取到的机会均等),记随机变量ξ为取出此2球所得分数之和,求ξ的分布列.(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若E(η)= ,D(η)= ,求a∶b∶c.(2)由题意知η的分布列为 规律方法 离散型随机变量的均值与方差的常见类型及解题策略(1)求离散型随机变量的均值与方差.可依题设条件求出离散型随机变量的分布列,然后利用均值、方差公式直接求解.(2)由已知均值或方差求参数值.可依据条件利用均值、方差公式得出含有参数的方程(组),解方程(组)即可求出参数值.变式训练2某滑雪场开展滑雪促销活动.该滑雪场的收费标准是:滑雪时间不超过1小时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过1小时离开的概率分别为 ;1小时以上且不超过2小时离开的概率分别为 ;两人滑雪时间都不会超过3小时.(1)求甲、乙两人所付滑雪费用相同的概率;(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).探究点三 均值与方差在决策中的应用【例3】 计划在某水库建一座至多安装3台发电机的水电站.过去50年的水文资料显示,水库年入流量X(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的入流量相互独立.(1)求未来4年中,至多有1年的年入流量超过120的概率;(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量X限制,并有如下关系:若某台发电机运行,则该台发电机年利润为5 000万元;若某台发电机未运行,则该台发电机年亏损800万元.欲使水电站年总利润的均值达到最大,应安装发电机多少台?(2)记水电站年总利润为Y(单位:万元).①安装1台发电机的情形.由于水库年入流量总大于40,故一台发电机运行的概率为1,对应的年利润Y=5 000,E(Y)=5 000×1=5 000.②安装2台发电机的情形.依题意,当40120时,三台发电机运行,此时Y=5 000×3=15 000,因此P(Y=15 000)=P(X>120)=P3=0.1.由此得Y的分布列如下.所以,E(Y)=3 400×0.2+9 200×0.7+15 000×0.1=8 620.综上,欲使水电站年总利润的均值达到最大,应安装发电机2台.规律方法 随机变量的均值反映了随机变量取值的平均水平,方差反映了随机变量稳定于均值的程度,它们从整体和全局上刻画了随机变量,是生产实际中用于方案取舍的重要理论依据.一般先比较均值,若均值相同,再用方差来决定.本节要点归纳1.知识清单:(1)二项分布的均值、方差;(2)超几何分布的均值、方差.2.方法归纳:公式法.3.常见误区:(1)对随机变量的分布类型判断出错;(2)混淆公式.成果验收·课堂达标检测123451.下列说法正确的是( )A.离散型随机变量ξ的均值E(ξ)反映了ξ取值的概率的平均值B.离散型随机变量ξ的方差D(ξ)反映了ξ取值的平均水平C.离散型随机变量ξ的均值E(ξ)反映了ξ取值的平均水平D.离散型随机变量ξ的方差D(ξ)反映了ξ取值的概率的平均值C解析 由离散型随机变量的均值与方差的定义可知,C正确. 123452.已知随机变量X的分布列如下. 其中a,b,c成等差数列.若E(X)= ,则D(X)的值是( ) B123453.随机变量ξ的取值为0,1,2.若P(ξ=0)= ,E(ξ)=1,则D(ξ)= . 123454.某广场上有4盏装饰灯,晚上每盏灯都随机地闪烁红灯或绿灯,每盏灯出现红灯的概率都是 ,出现绿灯的概率都是 .记这4盏灯中出现红灯的数量为ξ,当这4盏装饰灯闪烁一次时,则ξ的均值为 . 解析 (方法一)ξ的所有可能取值为0,1,2,3,4,计算的具体结果如下表所示.12345123455.甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率为 .求:(1)甲恰好击中目标2次的概率;(2)乙至少击中目标2次的概率;(3)乙恰好比甲多击中目标2次的概率. 12345
第七章培优课——离散型随机变量的均值与方差的综合应用重难探究·能力素养全提升成果验收·课堂达标检测目录索引 重难探究·能力素养全提升探究点一 二项分布均值与方差的综合【例1】 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,在下落的过程中,每次遇到障碍物时,小球向左、右两边下落的概率分别是 ,小球最后落入A袋或B袋中.(1)分别求出小球落入A袋和B袋中的概率;(2)在容器的入口处依次放入4个小球,记ξ为落入B袋中的小球的个数,求ξ的分布列、均值和方差.规律方法 通过审题,明确判断出随机变量X(击中次数)服从二项分布是解题的关键,然后利用二项分布的均值和方差的计算公式即可求出E(X),D(X).变式训练1某运动员投篮命中率P=0.6.(1)求1次投篮命中次数ξ的均值与方差;(2)求重复5次投篮时,命中次数η的均值与方差.解 (1)投篮1次只有两种结果,投篮命中ξ=1,不中ξ=0,服从两点分布,其分布列为则E(ξ)=1×0.6=0.6,D(ξ)=(1-0.6)×0.6=0.24.(2)由题意,重复5次投篮,命中的次数η服从二项分布,即η~B(5,0.6).由二项分布均值与方差的计算公式知,E(η)=5×0.6=3,D(η)=5×0.6×0.4=1.2.探究点二 离散型随机变量的均值与方差的常见类型【例2】 设袋子中装有a个红球、b个黄球、c个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.(1)当a=3,b=2,c=1时,从该袋子中任取一个球,记下颜色后放回,再取一个球(每球取到的机会均等),记随机变量ξ为取出此2球所得分数之和,求ξ的分布列.(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若E(η)= ,D(η)= ,求a∶b∶c.(2)由题意知η的分布列为 规律方法 离散型随机变量的均值与方差的常见类型及解题策略(1)求离散型随机变量的均值与方差.可依题设条件求出离散型随机变量的分布列,然后利用均值、方差公式直接求解.(2)由已知均值或方差求参数值.可依据条件利用均值、方差公式得出含有参数的方程(组),解方程(组)即可求出参数值.变式训练2某滑雪场开展滑雪促销活动.该滑雪场的收费标准是:滑雪时间不超过1小时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过1小时离开的概率分别为 ;1小时以上且不超过2小时离开的概率分别为 ;两人滑雪时间都不会超过3小时.(1)求甲、乙两人所付滑雪费用相同的概率;(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).探究点三 均值与方差在决策中的应用【例3】 计划在某水库建一座至多安装3台发电机的水电站.过去50年的水文资料显示,水库年入流量X(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的入流量相互独立.(1)求未来4年中,至多有1年的年入流量超过120的概率;(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量X限制,并有如下关系:若某台发电机运行,则该台发电机年利润为5 000万元;若某台发电机未运行,则该台发电机年亏损800万元.欲使水电站年总利润的均值达到最大,应安装发电机多少台?(2)记水电站年总利润为Y(单位:万元).①安装1台发电机的情形.由于水库年入流量总大于40,故一台发电机运行的概率为1,对应的年利润Y=5 000,E(Y)=5 000×1=5 000.②安装2台发电机的情形.依题意,当40
相关资料
更多









