新教材2023_2024学年高中数学第8章成对数据的统计分析综合训练新人教A版选择性必修第三册

这是一份新教材2023_2024学年高中数学第8章成对数据的统计分析综合训练新人教A版选择性必修第三册，共17页。

第八章综合训练
一、选择题(本题共8小题,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在一项中学生近视情况的调查中,某校男生150名中有80名近视,女生140名中有70名近视,在检验这些中学生眼睛近视是否与性别有关联时,最有说服力的方法是 (　　)
A.平均数与方差
B.回归分析
C.独立性检验
D.概率
2.[2023江西兴国期中]两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其抽样数据列联表如表所示.
X
Y
合计
y1
y2
x1
a
b
a+b
x2
c
d
c+d
合计
a+c
b+d
a+b+c+d
则在下列四组数据中,分类变量X和Y之间关系最强的是(　　)
A.a=4,b=2,c=3,d=6
B.a=2,b=1,c=3,d=5
C.a=4,b=5,c=6,d=8
D.a=2,b=3,c=4,d=6
3.从某高中学生中选取10名学生,根据其身高(单位:cm)、体重(单位:kg)数据,得到体重y关于身高x的经验回归方程=0.85x-85,用来刻画回归效果的R2=0.6,则下列说法正确的是(　　)
A.这些学生的体重和身高具有非线性相关关系
B.这些学生的体重和身高具有线性相关关系
C.身高为170 cm的学生的体重一定为59.5 kg
D.这些学生的身高每增加0.85 cm,其体重约增加1 kg
4.下列关于回归分析的说法错误的是(　　)
A.经验回归直线一定过点()
B.在残差图中,残差比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C.残差平方和越小,模型的拟合的效果越好
D.若甲、乙两个模型的R2分别约为0.98和0.80,则模型乙的拟合效果更好
5.某地以“绿水青山就是金山银山”理念为引导,推进绿色发展,现要订购一批苗木,苗木长度与售价如表:
苗木长度x/厘米
38
48
58
68
78
88
售价y/元
16.8
18.8
20.8
22.8
24
25.8
由表可知,苗木长度x(单位:厘米)与售价y(单位:元)之间存在线性相关关系,经验回归方程为=0.2x+,则当苗木长度为150厘米时,售价大约为(　　)
A.33.3元 B.35.5元 C.38.9元 D.41.5元
6.变量x与y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5),变量u与v相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示变量y与x之间的样本相关系数,r2表示变量v与u之间的样本相关系数,则(　　)
A.r2 B.0 C.r2<0 D.r2=r1
7.某公司为了确定下一年投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售量y(单位:千件)的影响.现收集了近5年的年宣传费x(单位:万元)和年销售量y(单位:千件)的数据,其数据如下表所示,且y关于x的经验回归方程为x-8.2,则下列结论错误的是(　　)
x
4
6
8
10
12
y
1
5
7
14
18
A.x,y之间呈正相关关系
B.=2.15
C.该经验回归直线一定经过点(8,7)
D.当该种产品的年宣传费为20万元时,预测该种产品的年销售量为34 800件
8.[2023北京丰台期末]经验表明,某种树的高度y(单位:m)与胸径x(单位:cm)(树的主干在地面以上1.3米处的直径)具有线性相关关系.根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的经验回归方程为=0.25x+15.据此模型进行推测,下列结论正确的是 (　　)
A.y与x负相关
B.胸径为20 cm的树,其高度一定为20 m
C.经过一段时间,样本中一棵树的胸径增加1 cm,估计其高度增加0.25 m
D.样本数据(xi,yi)(i=1,2,…,n)中至少有一对满足经验回归方程=0.25x+15
二、选择题(本题共4小题,在每小题给出的选项中,有多项符合题目要求)
9.下列说法正确的是(　　)
A.样本相关系数r越大,两个变量之间的线性相关性越强
B.样本相关系数r与回归系数同号
C.当P(B)>0时,P(A|B)=P(A)是A与B相互独立的充要条件
D.正态曲线越“胖”,方差越小
10.某地响应号召,建立农业科技图书馆,供农民免费借阅,收集了近5年的借阅数据如下表:
年份
2018
2019
2020
2021
2022
年份代码x
1
2
3
4
5
年借阅量y/万册
4.9
5.1
5.5
5.7
5.8
根据上表,可得y关于x的经验回归方程为=0.24x+,则下列说法正确的是(　　)
A.=4.68
B.近5年借阅量估计以0.24万册/年的速度增长
C.x与y的样本相关系数r>0
D.2023年的借阅量一定不少于6.12万册
11.某校计划在课外活动中新增攀岩项目,为了解学生喜欢攀岩和性别是否有关联,面向学生开展了一次随机调查,其中参加调查的男、女生人数相同,男生喜欢攀岩的占80%,女生不喜欢攀岩的占70%,则(　　)
参考公式:χ2=.
α
0.05
0.01
xα
3.841
6.635
A.参与调查的学生中喜欢攀岩的男生人数比喜欢攀岩的女生人数多
B.参与调查的女生中喜欢攀岩的人数比不喜欢攀岩的人数多
C.若参与调查的男、女生人数均为100人,则依据α=0.01的独立性检验认为喜欢攀岩和性别有关联
D.无论参与调查的男、女生人数为多少,都可以依据α=0.01的独立性检验认为喜欢攀岩和性别有关联
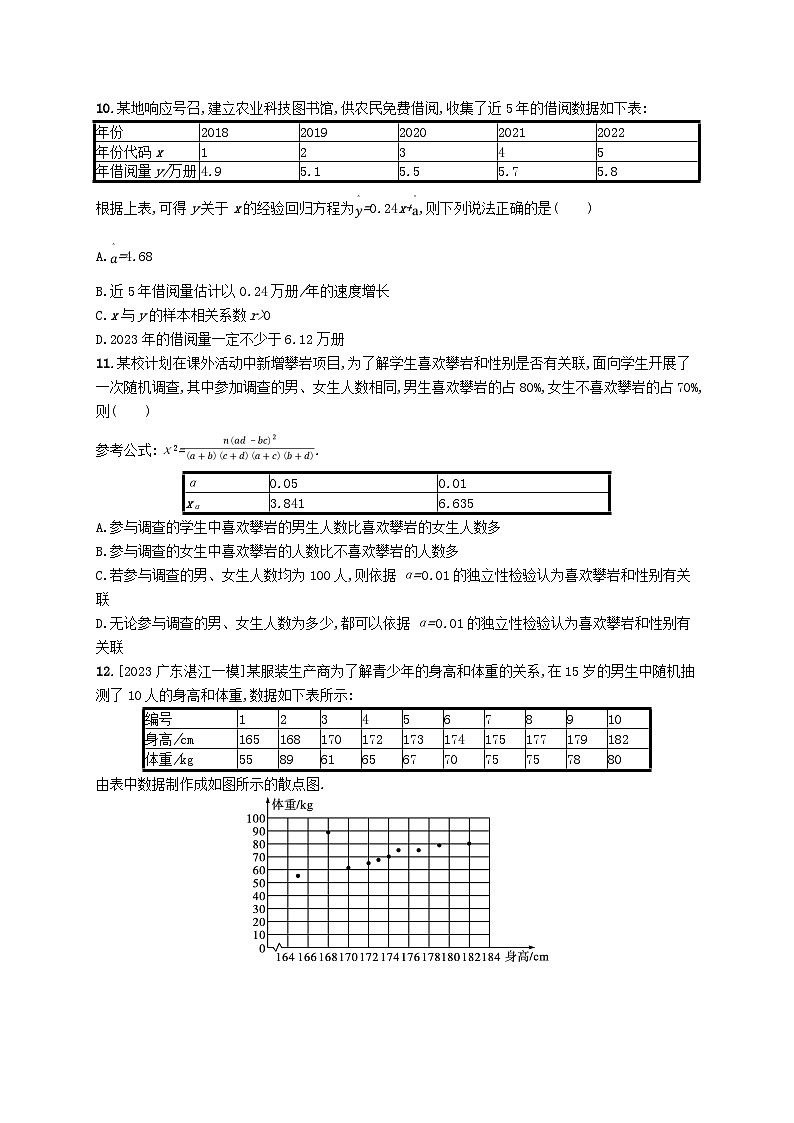
12.[2023广东湛江一模]某服装生产商为了解青少年的身高和体重的关系,在15岁的男生中随机抽测了10人的身高和体重,数据如下表所示:
编号
1
2
3
4
5
6
7
8
9
10
身高/cm
165
168
170
172
173
174
175
177
179
182
体重/kg
55
89
61
65
67
70
75
75
78
80
由表中数据制作成如图所示的散点图.

由最小二乘法计算得到经验回归直线l1的方程为x+,样本相关系数为r1,决定系数为;经过残差分析确定(168,89)为离群点(对应残差过大),把它去掉后,再用剩下的9组数据计算得到经验回归直线l2的方程为x+,样本相关系数为r2,决定系数为.则以下结论正确的有(　　)
A.r1>0,r2>0 B.
C.r1 三、填空题(本题共4小题)
13.某高校“统计初步”课程的教师随机统计了一些学生的情况,具体数据如下表:
性别
不选该课程
选择该课程
男
13
10
女
7
20
根据表中的数据,依据α=0.05的独立性检验,认为选择该门课程与性别　　　　　关联.(填“有”或“没有”) 
14.若一组观测值(x1,y1),(x2,y2),…,(xn,yn)之间满足yi=bxi+a+ei(i=1,2,…,n),且ei=0,则R2为　　　　　. 
15.某厂2023年1~4月份用水量(单位:百吨)的一组数据如下表:
月份x
1
2
3
4
用水量y
2.5
3
4
4.5
根据上表可画出散点图(图略),由散点图可知,用水量y与月份x之间有较明显的线性相关关系,其经验回归方程是x+1.75,则预测2023年6月份该厂的用水量为　　　　　百吨. 
16.下面是一个2×2列联表:
X
Y
合计
y1
y2
x1
a
21
70
x2
5
c
30
合计
b
d
100
则b-d=　　　　　,χ2≈　　　　　.(保留小数点后3位) 
四、解答题(本题共6小题,解答应写出文字说明、证明过程或演算步骤)
17.[2023湖南宜章检测]某公司市场部对同类产品连续5个月的销售单价x和月销售量y的数据进行了统计,得如下统计表:
月销售单价x/(元/件)
1
2
3
4
5
月销售量y/万件
28
23
m
15
10
统计时,不慎将m处的数据丢失,但记得0 (1)已知x和y线性相关,建立y关于x的经验回归方程;
(2)根据(1)的结果,若该产品成本是0.5元/件,月销售单价x(其中x∈N*)为何值时,公司月利润的预测值最大?
经验回归方程x+中斜率和截距的最小二乘估计为.













18.[2023安徽凤阳质检]已知甲、乙两地生产同一种瓷器,现从两地的瓷器中随机抽取了一共300件统计质量指标值,得到如图所示的两个统计图,其中甲地瓷器的质量指标值在区间[95,105]和[125,135]上的频数相等.
甲地瓷器质量频率分布直方图

乙地瓷器质量扇形图

(1)求频率分布直方图中x的值,并估计甲地瓷器质量指标值的平均值;(同一组中的数据用该组区间的中点值作代表)
(2)规定该种瓷器的质量指标值不低于125为特等品,且已知样本中甲地的特等品比乙地的特等品多10个,结合乙地瓷器质量扇形图完成下面的2×2列联表,并依据α=0.05的独立性检验,分析甲、乙两地的瓷器质量是否有差异.
单位:件
质量指标
特等品
非特等品
合计
甲地



乙地



合计



附:χ2=,其中n=a+b+c+d.
α
0.1
0.05
0.01
xα
2.706
3.841
6.635












19.为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表.记成绩不低于70分者为“成绩优良”.
分数
[50,59)
[60,69)
[70,79)
[80,89)
[90,100]
甲班频数
5
6
4
4
1
乙班频数
1
3
6
5
5
(1)由以上统计数据填写下面2×2列联表,依据α=0.05的独立性检验,能否认为成绩优良与教学方式有关联?
单位:人
成绩
班级
合计
甲班
乙班
优良



不优良



合计



(2)现从上述40人中,学校按成绩是否优良采用分层随机抽样的方法抽取8人进行考核.在这8人中,记乙班成绩不优良的人数为X,求X的分布列及数学期望.
附:χ2=.
α
0.1
0.05
0.01
xα
2.706
3.841
6.635












20.“碳中和”是指在一定时间内直接或间接产生的温室气体排放总量通过植树造林、节能减排等方式,以抵消自身产生的二氧化碳排放量,实现二氧化碳“零排放”.某城市计划通过绿色能源(光伏、风电、核能)替代煤电能源、智慧交通、大力发展新能源汽车以及植树造林置换大气中的二氧化碳实现碳中和.该城市某研究机构统计了若干小排量汽车5年内所行驶的里程数(单位:万千米)的频率分布直方图,如图.

(1)求a的值及这些汽车5年内所行驶里程的平均值.
(2)据“碳中和罗盘”显示:一辆小排量汽车每年行驶1万千米的排碳量需要近100棵树用1年时间来吸收.根据频率分布直方图,该城市每一辆小排量汽车平均每年需要多少棵树才能够达到“碳中和”?
(3)该城市为了减少碳排量,计划大力推动新能源汽车,关于车主购买汽车时是否考虑对大气污染的因素,对400名车主进行了调查,这些车主中新能源汽车车主占,且这些车主在购车时考虑大气污染因素的占20%,燃油汽车车主在购车时考虑大气污染因素的占15%,根据以上统计情况,补全下面2×2列联表,并依据小概率值α=0.01的独立性检验,分析购买新能源汽车与考虑大气污染是否有关联.
单位:人
车主
是否考虑大气污染
合计
考虑大气污染
没考虑大气污染
新能源汽车车主



燃油汽车车主



合计



附:χ2=,其中n=a+b+c+d.
α
0.1
0.05
0.01
0.005
0.001
xα
2.706
3.841
6.635
7.879
10.828











21.某医疗队针对某非洲国家制定的猴痘病毒防控措施之一是要求猴痘病毒确诊患者的密切接触者集中医学观察21天.在医学观察期结束后发现密切接触者中未接种过天花疫苗者感染病毒的比例较大.对该国家200个接种与未接种天花疫苗的密切接触者样本医学观察结束后,统计了感染病毒情况,得到下面的列联表:
单位:人
天花疫苗
猴痘病毒
合计
感染
未感染
未接种
30
60
90
接种
20
90
110
合计
50
150
200

(1)依据α=0.01的独立性检验,分析密切接触者感染猴痘病毒与未接种天花疫苗是否有关联.
(2)以样本中结束医学观察的密切接触者感染猴痘病毒的频率估计概率.现从该国所有结束医学观察的密切接触者中随机抽取4人进行感染猴痘病毒人数统计,求其中至多有2人感染猴痘病毒的概率.
(3)该国现有一个中风险村庄,当地政府决定对村庄内所有住户进行排查.在排查期间,发现一户3口之家与确诊患者有过密切接触,这种情况下医护人员要对其家庭成员逐一进行猴痘病毒检测.每名成员进行检测后即告知结果,若检测结果呈阳性,则该家庭被确定为“感染高危家庭”.假设该家庭每个成员检测呈阳性的概率均为p(0 附:χ2=,n=a+b+c+d.
α
0.1
0.05
0.01
xα
2.706
3.841
6.635










22.近期某公交公司分别推出扫码支付乘车活动,活动设置了一段时间的推广期.由于推广期内优惠力度较大,吸引了越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),统计数据如下表所示:
x
1
2
3
4
5
6
7
y
6
11
21
34
66
101
196

根据以上数据,绘制了散点图.

(1)根据散点图判断,在推广期内,y=a+bx与y=cdx(c,d均为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的经验回归方程模型;(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中的数据,求y关于x的经验回归方程,并预测活动推出第8天使用扫码支付的人次.
参考数据:其中vi=lg yi,vi


xiyi
xivi
100.54
62.14
1.54
2 535
50.12
3.47
参考公式:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其经验回归方程u的斜率和截距的最小二乘估计分别为.


参考答案
第八章综合训练
1.C
2.A　对于A,计算χ2=≈1.607,
对于B,计算χ2=≈0.749,
对于C,计算χ2=≈0.006,
对于D,计算χ2==0,
由题意知,选项A中观测值χ2最大,所以选项A中分类变量X和Y之间的关系最强.
3.B　因为经验回归方程为=0.85x-85,且刻画回归效果的R2=0.6,所以这些学生的体重和身高具有线性相关关系,故A错误,B正确;当x=170时,=0.85×170-85=59.5,预测身高为170 cm的学生体重为59.5 kg,故C错误;这些学生的身高每增加0.85 cm,其体重约增加0.85×0.85=0.722 5(kg),故D错误.
故选B.
4.D　对于A,经验回归直线一定过点(),正确;
对于B,可用残差图判断模型的拟合效果,残差比较均匀地落在水平的带状区域中,说明这样的模型比较合适,带状区域的宽度越窄,说明模型的拟合精度越高,故正确;
对于C,可用残差平方和判断模型的拟合效果,残差平方和越小,模型的拟合效果越好,故正确;
对于D,因为R2取值越大,说明残差平方和越小,模型的拟合效果越好,又因为甲、乙两个模型的R2分别约为0.98和0.80,且0.98>0.80,所以甲模型的拟合效果好,故D错误.
故选D.
5.C　由题意可知,×(38+48+58+68+78+88)=63,
×(16.8+18.8+20.8+22.8+24+25.8)=21.5,
因为经验回归直线=0.2x+过点(63,21.5),
则有21.5=0.2×63+,解得=8.9,
所以经验回归方程为=0.2x+8.9,
把x=150代入方程可得,=0.2×150+8.9=38.9.
所以当苗木长度为150厘米时,售价大约为38.9元.
6.C　∵变量x与y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5),
可得变量y与x之间正相关,∴r1>0.
变量u与v相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1),可知变量v与u之间负相关,
∴r2<0.
∴r2<0 7.C　由表中数据可得,×(4+6+8+10+12)=8,×(1+5+7+14+18)=9,
故经验回归直线一定经过点(8,9),
故9=8-8.2,解得=2.15,故A,B正确,C错误,
将x=20代入=2.15x-8.2,解得=34.8,
故当该种产品的年宣传费为20万元时,预测该种产品的年销售量为34 800件,故D正确.
故选C.
8.C　由经验回归方程=0.25x+15,可知y与x正相关,故A错误;
取x=20,得=0.25×20+15=20,说明胸径为20 cm的树,预测其高度为20 m,但也不一定就是20 m,故B错误;
样本中一棵树的胸径增加1 cm,估计其高度增加0.25 m,故C正确;
经验回归直线恒过样本点的中心,但样本中的点不一定经过经验回归直线,故D错误.
9.BC　样本相关系数r∈[-1,1],|r|越大,两个变量之间的线性相关性越强,故A错误.
样本相关系数r为正时,则两个变量为正相关,故回归系数为正,样本相关系数r为负时,则两个变量为负相关,故回归系数为负,故样本相关系数r与回归系数同号,故B正确.
当P(B)>0时,若P(A|B)=P(A),则由P(A|B)=,得P(A)=,
即P(AB)=P(A)P(B),故A与B相互独立;
若A与B相互独立,则P(AB)=P(A)P(B),因为P(B)>0,所以P(A|B)==P(A).
所以当P(B)>0时,P(A|B)=P(A)是A与B相互独立的充要条件,故C正确.
正态曲线越“胖”,说明随机变量的取值越分散,故方差越大,故D错误.
10.ABC　把=3,=5.4代入=0.24x+,可得=4.68,故A正确;
由=0.24x+,得直线的斜率为0.24,0.24万册是每年的借阅量的增长量的预测值,故B正确;
因为=0.24>0,所以x与y正相关,故r>0,故C正确;
把x=6代入=0.24x+4.68,得=6.12,然而6.12万册是预测值,不是精确值,故D错误.
故选ABC.
11.AC　由题意设参加调查的男、女生人数均为m人,则得到如下2×2列联表:
单位:人
性别
喜欢攀岩
不喜欢攀岩
合计
男生
0.8m
0.2m
m
女生
0.3m
0.7m
m
合计
1.1m
0.9m
2m
所以参与调查的学生中喜欢攀岩的男生人数比喜欢攀岩的女生人数多,参与调查的女生中喜欢攀岩的人数比不喜欢攀岩的人数少,故A正确,B错误.
零假设为H0:喜欢攀岩和性别无关联.由列联表中的数据,计算得到χ2=,当m=100时,χ2=≈50.505>6.635=x0.01,所以当参与调查的男、女生人数均为100人时,依据α=0.01的独立性检验,我们推断H0不成立,即认为喜欢攀岩和性别有关联,此推断犯错误的概率不超过0.01,故C正确,D错误.故选AC.
12.AC　结合题中图象,可知身高和体重正相关,故A正确;
因为离群点(168,89)的纵坐标89相对过大,所以去掉离群点后经验回归直线的截距变小,所以,故B错误;
去掉离群点后成对样本数据的线性相关程度更强,拟合效果会更好,所以r1 13.有　零假设为H0:选择该门课程与性别无关联.根据表中的数据,得到χ2=≈4.84>3.841=x0.05,依据α=0.05的独立性检验,我们推断H0不成立,即认为选择该门课程与性别有关联,此推断犯错误的概率不超过0.05.
14.1　由ei=0,知yi=,即yi-=0,
故R2=1-=1-0=1.
15.5.95　由题意可知=2.5,
=3.5.
又因为经验回归直线经过(),所以3.5=2.5+1.75,
解得=0.7.
所以=0.7x+1.75.
当x=6时,=0.7×6+1.75=5.95.
所以预测2023年6月份该厂的用水量为5.95百吨.
16.8　24.047　由2×2列联表得a=49,b=54,c=25,d=46.
∴b-d=54-46=8.
χ2=≈24.047.
17.解∵月销售量的平均数与中位数相等,且平均数>15,
∴中位数为m或23,则=m或=23,解得m=19或m=39(舍去).
(1)=3,=19.
xiyi=1×28+2×23+3×19+4×15+5×10=241,
=-4.4,=19-(-4.4)×3=32.2.
∴y关于x的经验回归方程为=-4.4x+32.2.
(2)设销售利润为z,则z=(x-0.5)(-4.4x+32.2)(x>0.5且x∈N*),
∴z=-4.4x2+34.4x-16.1,≈3.9,
∴当x=4时,z取最大值.
∴月销售单价为4元/件时,公司月利润的预测值最大.
18.解(1)由(0.008+x+0.026+0.03+x+0.004)×10=1,解得x=0.016.
甲地瓷器质量指标的平均值为=90×0.08+100×0.16+110×0.26+120×0.3+130×0.16+140×0.04=114.2.
(2)设300件样品中甲地瓷器有m件,则乙地瓷器有(300-m)件,因为甲地的特等品比乙地的特等品多10个,从而有0.2m-(300-m)×30%=10,解得m=200.
零假设为H0:甲、乙两地的瓷器质量没有差异.
从而2×2列联表如下:
单位:件
质量指标
特等品
非特等品
合计
甲地
40
160
200
乙地
30
70
100
合计
70
230
300
所以χ2=≈3.727<3.841=x0.05,所以依据α=0.05的独立性检验,没有充分证据推断H0不成立,因此认为H0成立,即认为甲、乙两地的瓷器质量没有差异.
19.解(1) 单位:人
成绩
班级
合计
甲班
乙班
优良
9
16
25
不优良
11
4
15
合计
20
20
40
零假设为H0:成绩优良与教学方式无关联.根据2×2列联表中的数据,可得χ2=≈5.227>3.841=x0.05,依据α=0.05的独立性检验,我们推断H0不成立,即认为成绩优良与教学方式有关联,此推断犯错误的概率不大于0.05.
(2)由列联表可知在8人中成绩不优良的人数为×8=3,则X的可能取值为0,1,2,3.
P(X=0)=;P(X=1)=;
P(X=2)=;P(X=3)=.
所以X的分布列为
X
0
1
2
3
P




E(X)=0×+1×+2×+3×.
20.解 (1)由(0.052+a+0.32+0.22+a+0.052)×1=1,解得a=0.178.
设为这些汽车5年内所行驶里程的平均值,则=3.5×0.052+4.5×0.178+5.5×0.32+6.5×0.22+7.5×0.178+8.5×0.052=5.95.
(2)由(1)可知,一辆汽车1年内平均行驶里程为=1.19(万千米),因为一辆汽车每年行驶1万千米的排碳量需要近100棵树用1年时间来吸收,所以每一辆汽车平均需要1.19×100=119(棵)树才能够达到“碳中和”.
(3)对400名车主进行了调查,这些车主中新能源汽车车主有400×=80(人),这些车主在购车时考虑大气污染因素的占80×20%=16(人),燃油汽车车主有400×=320(人),燃油汽车车主在购车时考虑大气污染因素的有320×15%=48(人),
补全2×2列联表如下:
单位:人
车主
是否考虑大气污染
合计
考虑大气污染
没考虑大气污染
新能源汽车车主
16
64
80
燃油汽车车主
48
272
320
合计
64
336
400
零假设为H0:购买新能源汽车与考虑大气污染无关联.
因为χ2=≈1.19<6.635=x0.01,所以根据小概率值α=0.01的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为购买新能源汽车与考虑大气污染无关联.
21.解(1)零假设为H0:密切接触者感染猴痘病毒与未接种天花疫苗无关联.
依题意知,χ2=≈6.061<6.635=x0.01,所以依据α=0.01的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为密切接触者感染猴痘病毒与未接种天花疫苗无关联.
(2)由题意得,该地区每名密切接触者感染病毒的概率为.
设随机抽取的4人中至多有2人感染病毒为事件A,
则P(A)=1-×3×-4=.
(3)设事件B为该家庭检测了2名成员确定为“感染高危家庭”;事件C为该家庭检测了3名成员确定为“感染高危家庭”,
则P(B)=(1-p)p,P(C)=(1-p)2p,
所以f(p)=(1-p)p+(1-p)2p=p(1-p)(2-p),
设x=1-p,x>0,则p=1-x,所以y=(1-x)x(1+x)=x-x3,
对其求导得y'=1-3x2,令y'=0,得x=,此时p=1-,f(p)取得最大值.
22.解(1)根据散点图判断y=cdx适宜作为扫码支付的人次y关于活动推出天数x的经验回归方程模型.
(2)由(1)知y=cdx,两边同时取对数得lgy=lgc+(lgd)·x,设v=lgy,
则=4,=12+22+32+42+52+62+72=140,
所以lgd==0.25,
所以lgc=-(lg d)·=1.54-0.25×4=0.54.
所以v关于x的经验回归方程为=0.54+0.25x,则y关于x的非线性经验回归方程为=100.54+0.25x=3.47×100.25x,当x=8时,=3.47×102=347,故预测活动推出第8天使用扫码支付的人次为347.