第二十四章圆习题24.2课件（人教版九上）

这是一份第二十四章圆习题24.2课件（人教版九上），共15页。

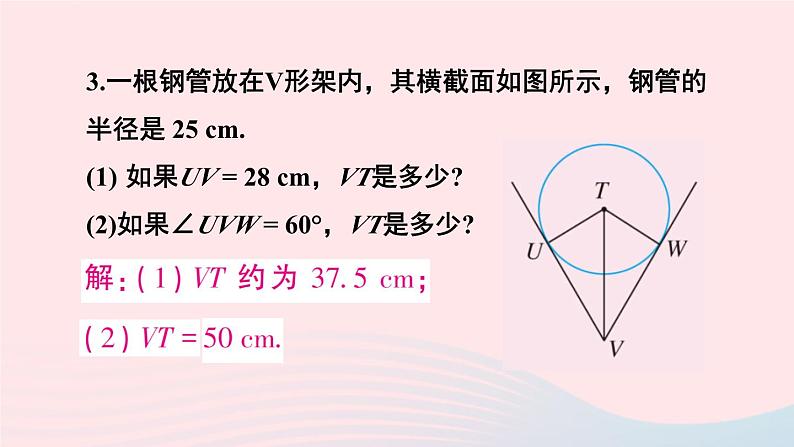
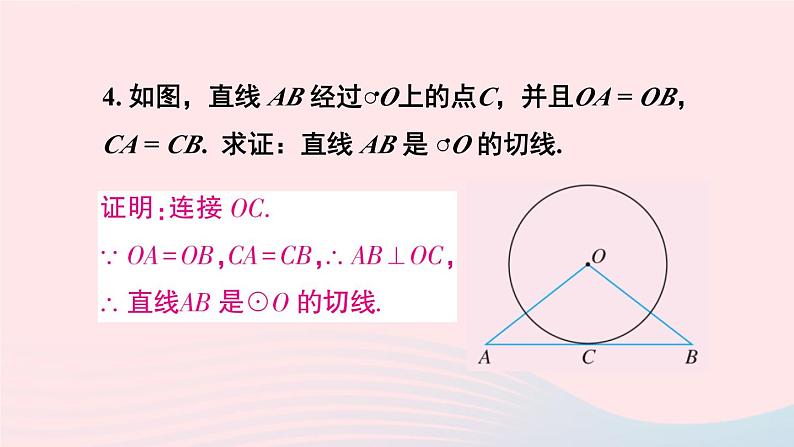
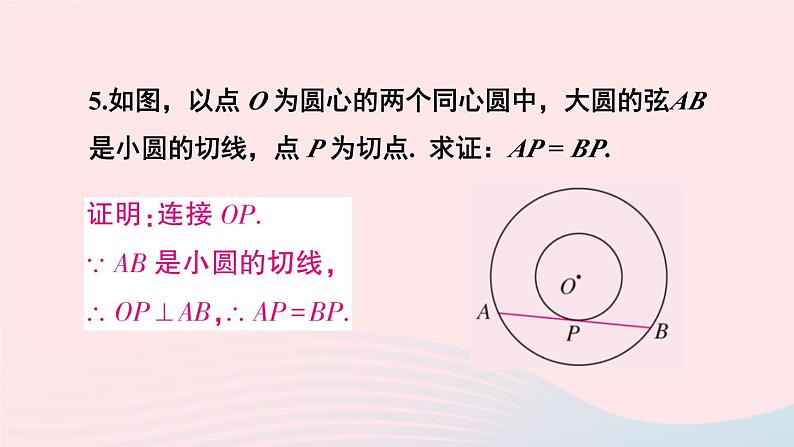
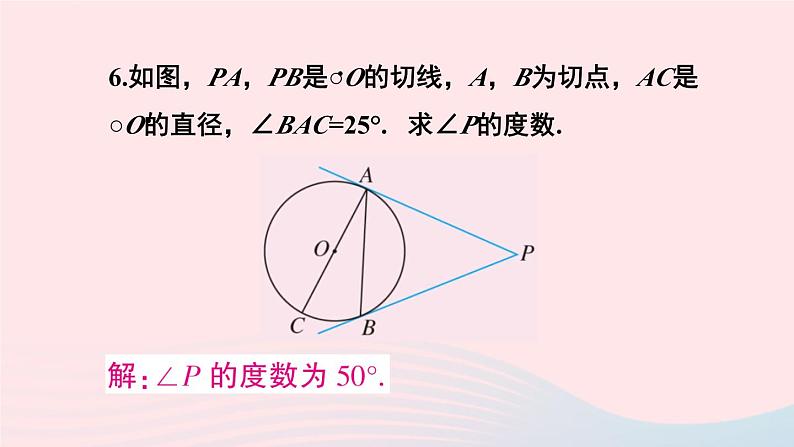
习题 24.2R·九年级上册复习巩固1. ○O的半径为10 cm，根据下列点 P 到圆心 O 的距离，判断点 P 和○O的位置关系：(1)8cm； (2)10cm； (3)12cm.··3.一根钢管放在V形架内，其横截面如图所示，钢管的半径是 25 cm.如果UV = 28 cm，VT是多少?(2)如果∠UVW = 60°，VT是多少?4. 如图，直线 AB 经过○O上的点C，并且OA = OB，CA = CB. 求证：直线 AB 是 ○O 的切线.··5.如图，以点 O 为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点 P 为切点. 求证：AP = BP.6.如图，PA，PB是○O的切线，A，B为切点，AC是○O的直径，∠BAC=25°. 求∠P的度数.··综合运用7.已知 AB = 6cm，画半径为4 cm的圆，使它经过A，B两点. 这样的圆能画出多少个？如果半径为 3cm，2cm 呢？8. 如图，分别作出锐角三角形、直角三角形和钝角三角形的外接圆，它们外心的位置有什么特点？9.如图是一名考古学家发现的一块古代车轮的碎片，你能帮他找出这个轮子的半径吗？说出你的理由.10. 如图，一个油桶靠在直立的墙边，量得WY = 0.65 m，并且XY⊥WY. 这个油桶的底面半径是多少？为什么？11.如图，AB，BC，CD分别与○O相切于 E，F，G三点，且AB // CD， BO = 6 cm，CO = 8 cm. 求，BC的长.·12. 如图，AB为○O的直径，C为○O上一点，AD和过点C的切线互相垂直，垂足为D. 求证：AC平分∠DAB.··拓广探索13. 如下页图，等圆 ○O1 和 ○O2 相交于A，B两点，○O1经过○O2的圆心O2. 求∠O1AB的度数.····14. 如图，Rt△ABC中，∠C = 90°，AB，BC，CA的长分别为c，a，b. 求△ABC的内切圆半径 r .