北师大版七年级数学下册专题三第二章相交线与平行线创新考点教学课件

这是一份北师大版七年级数学下册专题三第二章相交线与平行线创新考点教学课件，共16页。
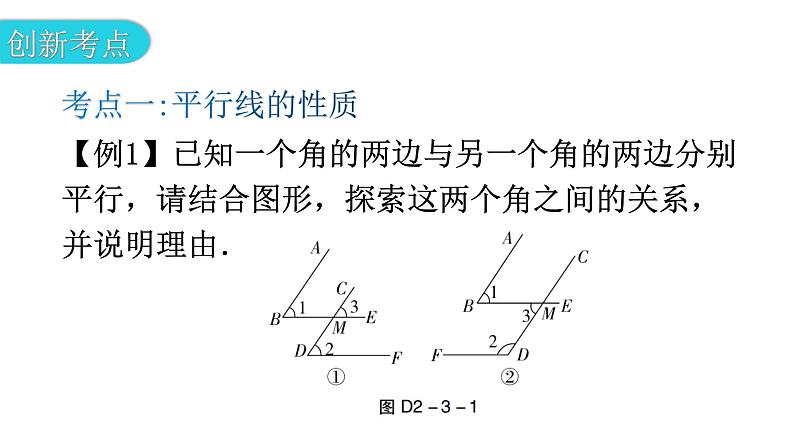
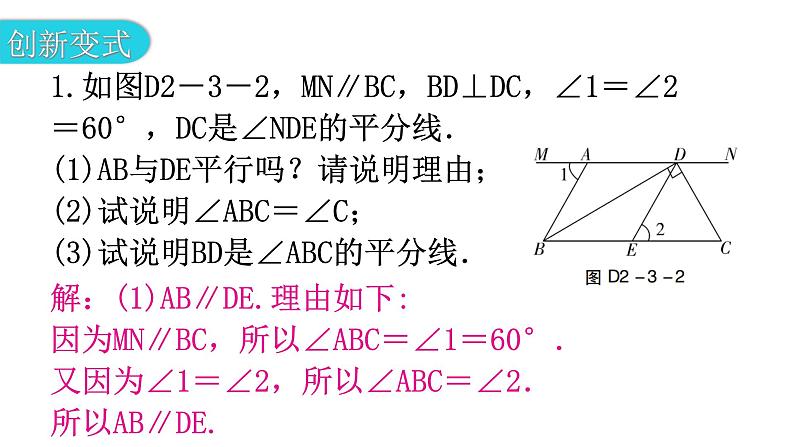
专题三 本章创新考点【例1】已知一个角的两边与另一个角的两边分别平行，请结合图形，探索这两个角之间的关系，并说明理由． 考点一:平行线的性质(1)如图D2－3－1①，AB∥CD，BE∥DF，∠1与∠2的关系是什么？请说明理由;(2)如图D2－3－1②，AB∥CD，BE∥DF，∠1与∠2的关系是什么？请说明理由；(3)经过上述论证，我们可得出结论，如果一个角的两边与另一个角的两边分别平行，那么这两个角________________；相等或互补(4)若这两个角的两边分别平行，且一个角比另一个角的2倍少30°，则这两个角分别是多少度？解：(1)∠1与∠2相等. 理由如下：因为AB∥CD，所以∠1＝∠3.因为BE∥DF，所以∠2＝∠3. 所以∠1＝∠2.（2）∠1与∠2互补.理由如下：因为AB∥CD，所以∠1＝∠3.因为BE∥DF，所以∠2＋∠3＝180°.所以∠1＋∠2＝180°.(4)设一个角的度数为x，则另一个角的度数为2x－30°.①当x＝2x－30°，解得x＝30°，则这两个角的度数分别为30°，30°；②当x＋2x－30°＝180°，解得x＝70°，则这两个角的度数分别为70°，110°.1.如图D2－3－2，MN∥BC，BD⊥DC，∠1＝∠2＝60°，DC是∠NDE的平分线．(1)AB与DE平行吗？请说明理由；(2)试说明∠ABC＝∠C；(3)试说明BD是∠ABC的平分线．解：(1)AB∥DE.理由如下:因为MN∥BC，所以∠ABC＝∠1＝60°．又因为∠1＝∠2，所以∠ABC＝∠2．所以AB∥DE.【例2】如图D2－3－3，直线MN分别与直线AC，DG交于点B，F，且∠1＝∠2．∠ABF的平分线BE交直线DG于点E，∠BFG的平分线FC交直线AC于点C. (1)请写出直线AC与DG的位置关系，并说明理由；(2)求证：BE∥CF；(3)若∠C＝35°，求∠BED的度数．考点二：平行线的判定解：(1)AC∥DG. 理由如下：因为∠ABF＝∠1，∠1＝∠2，所以∠ABF＝∠2.所以AC∥DG. (3)解：因为AC∥DG，∠C＝35°，所以∠C＝∠CFG＝35°. 因为BE∥CF，所以∠BEG＝∠CFG＝35°. 所以∠BED＝180°－∠BEG＝145°．2. 如图D2－3－4，在三角形ABC中，D，E，F分别是三边上的点，且DE平分∠ADF，∠ADF＝2∠DFB. (1)求证：DE∥BC；(2)若∠B＝∠DEF，请判断EF和AB的位置关系，并说明理由；(3)在(2)的条件下，若∠BDF＝2∠B，求∠B的大小．(1)证明：因为DE平分∠ADF，所以∠ADF＝2∠EDF. 又因为∠ADF＝2∠DFB，所以∠EDF＝∠DFB. 所以DE∥BC. (2)解：EF∥AB. 理由如下：因为DE∥BC，所以∠B＝∠ADE. 因为∠B＝∠DEF，所以∠ADE＝∠DEF. 所以EF∥AB. (3)解：因为DE平分∠ADF，所以∠ADE＝∠EDF. 因为DE∥BC，所以∠B＝∠ADE，∠EDB＋∠B＝180°. 所以∠B＝∠EDF. 因为∠BDF＝2∠B，所以(∠B＋2∠B)＋∠B＝180°. 所以∠B＝45°．