初中数学北师大版九年级下册1 锐角三角函数巩固练习

这是一份初中数学北师大版九年级下册1 锐角三角函数巩固练习，共39页。
一、选择题（每题3分，共30分）
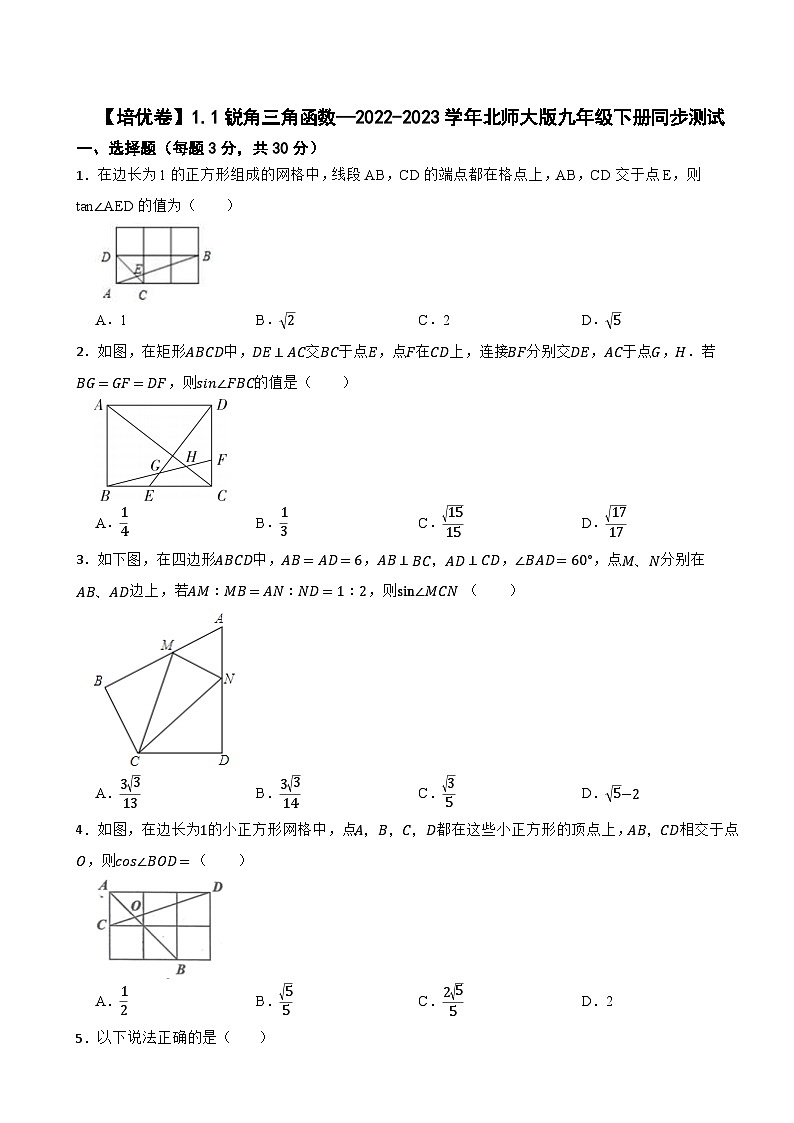
1．在边长为1的正方形组成的网格中，线段AB，CD的端点都在格点上，AB，CD交于点E，则tan∠AED的值为（ ）
A．1B．2C．2D．5
2．如图，在矩形ABCD中，DE⊥AC交BC于点E，点F在CD上，连接BF分别交DE，AC于点G，H．若BG=GF=DF，则sin∠FBC的值是（ ）
A．14B．13C．1515D．1717
3．如下图，在四边形ABCD中，AB=AD=6，AB⊥BC，AD⊥CD，∠BAD=60°，点M、N分别在AB、AD边上，若AM：MB=AN：ND=1：2，则sin∠MCN （ ）
A．3313B．3314C．35D．5−2
4．如图，在边长为1的小正方形网格中，点A，B，C，D都在这些小正方形的顶点上，AB，CD相交于点O，则cs∠BOD=（ ）
A．12B．55C．255D．2
5．以下说法正确的是（ ）
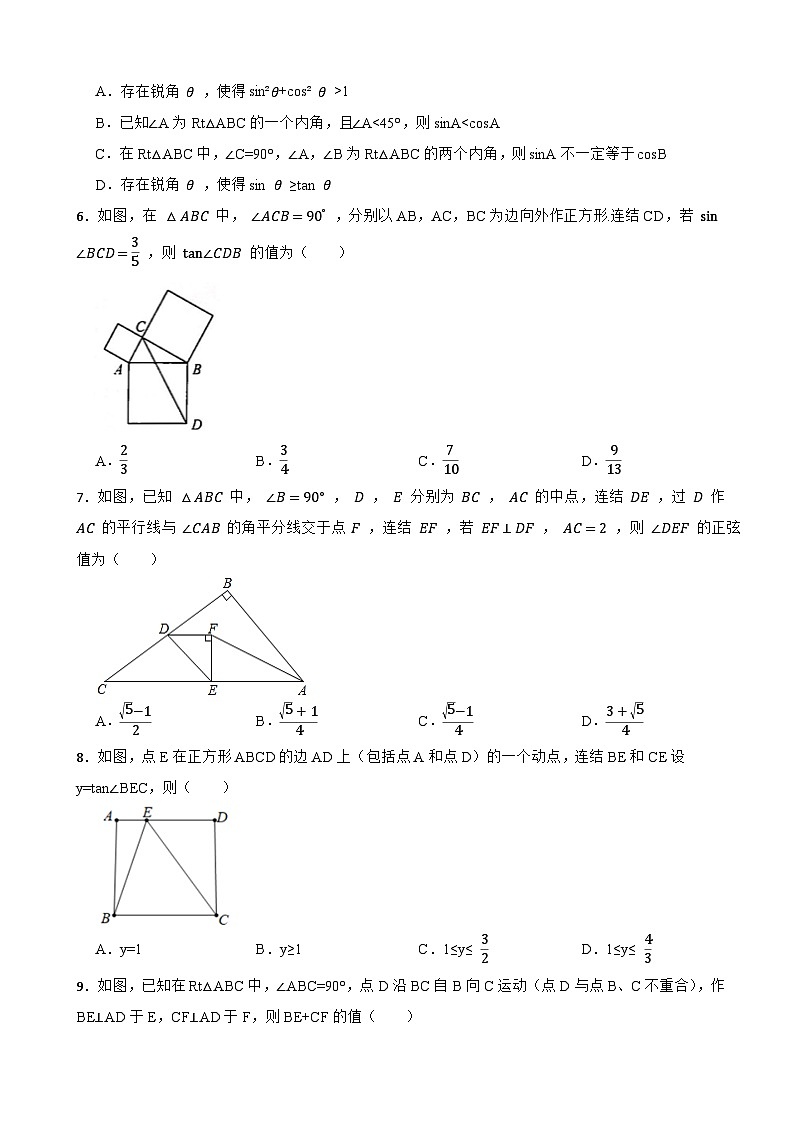
A．存在锐角 θ ，使得sin²θ+cs² θ >1
B．已知∠A为Rt△ABC的一个内角，且∠A0，x>0)的图象有且只有一个交点B，一次函数y＝－x＋2a与x轴交于点A，点P是线段OA上的动点，点Q在反比例函数图象上，且满足∠BPO＝∠QPA．设PQ与线段AB的交点为M，若OM⊥BP，则sin∠AMP的值为 ．
三、解答题（共7题，共66分）
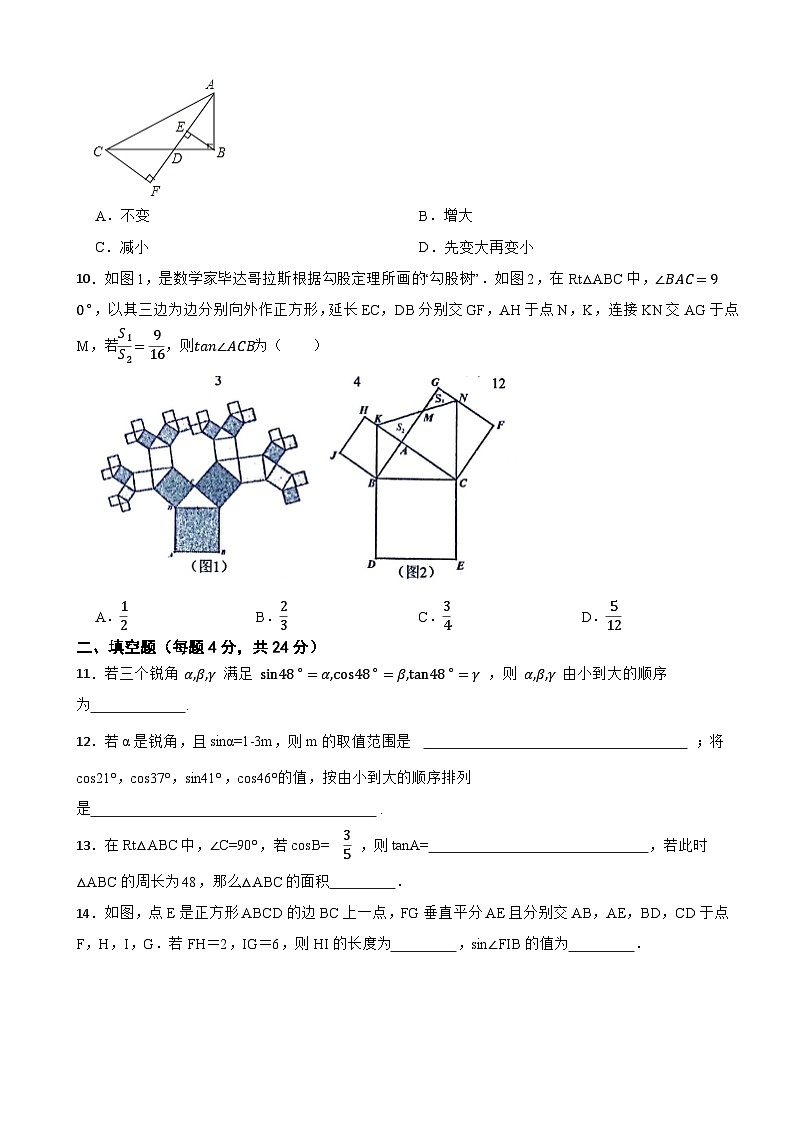
17．△ABC 中，tan∠ACB=m，AD⊥BC于D，CE⊥AB于E，AD交CE于F
（1）求证：△ADC∽△BDF；
（2）求sin∠FBD（用含m的代数式表示）；
（3）当m=43时，求CECF的最大值．
18．如图
（1）如图1，在△ABC中，∠ACB=2∠B，CD平分∠ACB，交AB于点D，DE//AC，交BC于点E．
①若DE=1，BD=32，求BC的长；
②试探究ABAD−BEDE是否为定值．如果是，请求出这个定值；如果不是，请说明理由．
（2）如图2，∠CBG和∠BCF是△ABC的2个外角，∠BCF=2∠CBG，CD平分∠BCF，交AB的延长线于点D，DE//AC，交CB的延长线于点E.记△ACD的面积为S1，△CDE的面积为S2，△BDE的面积为S3.若S1⋅S3=916S22，求cs∠CBD的值．
19．已知，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，点M是射线CD上一动点（不与C、D重合），连结AM，在AM下方作△AMN，连结BN，使∠MAN=∠CAB，∠ABN=∠ABC．
（1）如图，当点M在线段CD上时，求证：△ACM∽△ABN；
（2）如图，AC∶BC=3∶4，当点M在线段CD的延长线上时，BN交射线CD于点E．
①试判断AM与MN的数量关系和位置关系，并说明理由；
②若BN=AB，求sin∠ENM的值．
20．如图，在矩形ABCD中，AE平分∠BAD交射线BC于点E，过点C作CF⊥AE交射线AE于点F，连结BD交AE于点G，连结DF交射线BC于点H.
（1）当AB＜AD时，
①求证：BE＝CD，
②猜想∠BDF的度数，并说明理由.
（2）若ABAD=k时，求tan∠CDF的值（用含k的代数式表示）.
21．（1）如图1，纸片▱ABCD中，AD＝10，S▱ABCD=60，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCE′的位置，拼成四边形AEE′D，则四边形AEE′D的形状为____．（从以下选项中选取）
A．正方形
B．菱形
C．矩形
（2）如图2，在（1）中的四边形纸片AEE′D中，在EE′上取一点F，使EF＝8， 剪下△AEF，将它平移至△DE′F′的位置，拼成四边形AFF′D．
①求证：四边形AFF′D是菱形；
②连接DF，求sin∠ADF的值．
22．如图，在矩形ABCD中，AD=nAB(n>1)，点E是AD边上一动点（点E不与A，D重合），连接BE，以BE为边在直线BE的右侧作矩形EBFG，使得矩形EBFG∽矩形ABCD，EG交直线CD于点H.
（1）【尝试初探】在点E的运动过程中，△ABE与△DEH始终保持相似关系，请说明理由.
（2）【深入探究】若n=2，随着E点位置的变化，H点的位置随之发生变化，当H是线段CD中点时，求tan∠ABE的值.
（3）【拓展延伸】连接BH，FH，当△BFH是以FH为腰的等腰三角形时，求tan∠ABE的值（用含n的代数式表示）.
23．问题背景：
（1）如图1，正方形ABCD，点E、F分别在边AB、BC上，连接AF与DE交于点O，有∠FOD＝90°，则AFDE＝ ，若E为AB中点，则EODO= ；
（2）尝试应用：
如图2，平行四边形ABCD，AB＝5，BC＝4，点E边AB上，点F在边BC的延长线上，连接AF与DE交于点O，当∠FOD＝∠B时，求AFDE的值；
（3）类比拓展：
如图3，菱形ABCD中，AEBE=2m（m>2），点E在边AB上，点F是BC延长线上一点，且满足BCCF=32，连接AF与DE交于点O时，∠DAO＝∠AED；直接写出cs∠ABF的值．（用含m的式子表示）
答案解析部分
1．【答案】C
【知识点】正方形的性质；相似三角形的判定与性质；锐角三角函数的定义
【解析】【解答】解：连结AF，交CD于点F，如图所示，
∵四边形ACGD是正方形，
∴DF=CF=12CD，GF=12AG，CD⊥AG，CD=AG，
∴DF=AF，
由题意得AC∥BD，
∴△ACE~△DBE，
∴CEDE=ACBD=13，
∴CECF=12，
∴CE=CF=12DF=12AF，
在Rt△AEF中，tan∠AED=AFEF=2，
故答案为：C.
【分析】连结AF，交CD于点F，由题意得出四边形ACGD是正方形，根据正方形的性质即可得出DF=CF=12CD，GF=12AG，CD⊥AG，CD=AG，然后根据AC∥BD，得出△ACE~△DBE，从而得出CEDE=ACBD=13，进而得出CECF=12，在Rt△AEF中，根据正切函数的定义即可求解.
2．【答案】A
【知识点】平行线的性质；等腰三角形的判定与性质；矩形的性质；锐角三角函数的定义；三角形的中位线定理
【解析】【解答】解：连接BD交AC于点O，连接OG，
∵BG=GF=DF，
∴∠FGD=∠FDG.
∵四边形ABCD为矩形，
∴OB=OD，AB=CD，∠ABC=∠BCD=90°，
∴OG为△BDF的中位线，
∴OG∥DC，DF=BG=GF=2OG，
∴∠ACD=∠COG.
∵∠FGD+∠OHG=90°，∠ACD+∠FDG=90°，
∴∠OHG=∠ACD.
∵∠OHG=∠CHF，
∴∠OHG=∠CHF=∠ACD=∠COG，
∴OG=GM，MF=FC.
设OG=GH=x，则DF=GF=2x，
∴HF=FC=GF-GH=x，CD=DF+CF=3x，
∴sin∠FBC=CFBF=x4x=14.
故答案为：A.
【分析】连接BD交AC于点O，连接OG，由已知条件可知BG=GF=DF，根据等腰三角形的性质可得
∠FGD=∠FDG，由矩形的性质可得OG为△BDF的中位线，则OG∥DC，DF=BG=GF=2OG，根据平行线的性质可得∠ACD=∠COG，由同角的余角相等结合对顶角的性质可得∠OHG=∠CHF=∠ACD=∠COG，则OG=GH，HF=FC，设OG=GH=x，则DF=GF=2x，HF=FC=GF-GH=x，CD=DF+CF=3x，然后利用三角函数的概念进行计算.
3．【答案】B
【知识点】直角三角形全等的判定（HL）；勾股定理；锐角三角函数的定义
【解析】【解答】如图，连接AC，连接MN，过M点作ME⊥CN于E，
∵AB=AD=6，AM：MB=AN：ND=1：2，
∴AM=AN=2，BM=DN=4，
∵AB⊥BC，AD⊥CD，∠BAD=60°，
在Rt△ABC与Rt△ADC中
AB=ADAC=AC，
∴Rt△ABC≌Rt△ADC（HL），
∴∠BAC=∠DAC=12BAD=30°，MC=NC，
∴BC=12AC，
∴AC2=BC2+AB2，
即(2BC)2=BC2+AB2，
BC=23，
在Rt△BMC中，
CM=BM2+BC2=42+(23)2=27，
∵AN=AM，∠MAN=60°，
∴△MAN是等边三角形，
∴MN=AM=AN=2，
设NE=x，则CE=27−x，
∴MN2−NE2=MC2−EC2，
即4−x2=(27)2−(27−x)2，
解得x=77，
∴ME=MN2−NE2=3217，
∴sin∠MCN=MECM=3314．
故答案为：B．
【分析】连接AC，通过三角形全等，求得∠BAC=30°，从而求得BC的长，然后根据勾股定理求得CM的长，连接MN，过点M作ME⊥CN于E，则△MNA是等边三角形求得MN=2，设NE=x，表示出CE，根据勾股定理即可求得ME，然后求得sin∠MCN的值即可。
4．【答案】B
【知识点】锐角三角函数的定义
【解析】【解答】解：连接CE、DE，如图：
∵由图可知：∠1=∠2=∠3=∠4=∠ABE=45°
∴∠CED=∠2+∠3=90°，AB//CE
∴∠BOD=∠DCE
∵小正方形的边长为1
∴在Rt△CDE中，CE=12+12=2， CD=12+32=10
∴cs∠DCE=CECD=210=55
∴cs∠BOD=cs∠DCE=55．
故答案为：B
【分析】先求出∠BOD=∠DCE，再利用勾股定理和锐角三角函数计算求解即可。
5．【答案】B
【知识点】互余两角三角函数的关系
【解析】【解答】解：A、因为对于任意角， sin²θ+cs²θ=1，不符合题意；
B、当∠A小于45°时，有 sinA