






还剩11页未读,
继续阅读
第四章因式分解本章章末复习课件(北师大版八下)
展开
这是一份第四章因式分解本章章末复习课件(北师大版八下),共19页。
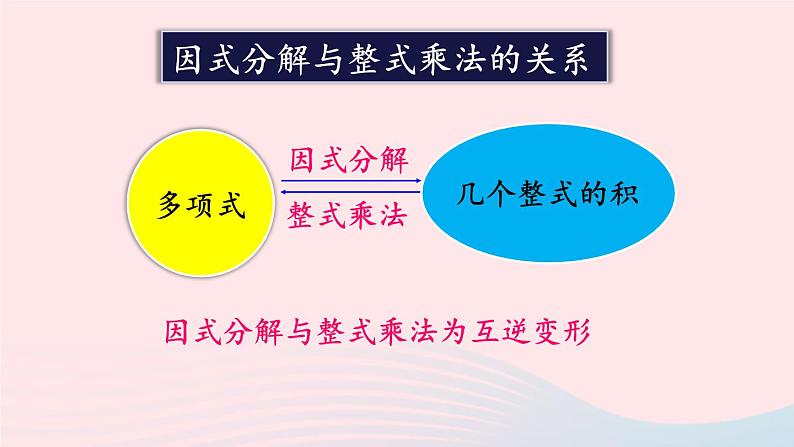
北师版 八年级下册本章章末复习因式分解的定义 把一个多项式化成_____________的形式,这种变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.几个整式的积因式分解与整式乘法的关系因式分解整式乘法因式分解与整式乘法为互逆变形因式分解的方法1.提公因式法 如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法.提公因式法的依据:____________________________.am + bm + cm = m(a + b + c)怎么确定公因式? 各项系数的最大公约数与各项相同字母(或因式)的最低次幂的积.2.公式法 (1) 平方差公式:a2 - b2 = (a + b)(a - b).即两个数的平方差,等于这两个数的和与这个数的差的积. (2)完全平方公式:a2±2ab + b2 = (a±b)2.其中,a2±2ab + b2 叫做完全平方式.思想方法归纳1.整体思想 如果将两个多项式相乘展开后项数太多,而两个多项式中又有相同部分,我们可以考虑将这一部分当成一个整体.因式分解: (x - 2)(x - 4)(x - 6)(x - 8) + 16.解: (x - 2)(x - 4)(x - 6)(x - 8) + 16= [(x - 2) (x - 8)][(x - 4)(x - 6)] + 16= [(x2 -10x) + 16][(x2 - 10x) + 24] + 16= (x2 - 10x)2 + 40(x2 - 10x) + 16×24 + 16= (x2 - 10x)2 + 40(x2 - 10x) + 202= (x2 - 10x + 20)2.2.转化思想 某些多项式从表面上看是无法利用因式分解的一般步骤进行的,需要通过适当的转化,如经过添“-”号、去括号、合并同类项等变形,才能利用因式分解的有关方法进行.把多项式 6x(x - y)2 + 3(y - x)3 因式分解.解:6x(x - y)2 + 3(y - x)3 = 6x(x - y)2 - 3(x - y)3 = 3(x - y)2[2x - (x - y)] = 3(x - y)2(x + y).3.换元思想 换元思想就是将较复杂的式子中的某些整体用新的字母代替,从而使计算简单化.多项式 (x2 + y2) (x2 - 2xy + y2) + x2y2 因式分解.解:设x2 + y2 = m,xy = n.则(x2 + y2) (x2 - 2xy + y2) + x2y2= m(m - 2n) + n2= m2 - 2mn + n2= (m-n)2 = (x2 + y2 - xy)2. 随堂练习将下列多项式因式分解,结果中不含有因 式a + 1的是( ). A. a2 - 1 B. a2 + a C. a2 + a - 2 D. (a + 2)2 - 2(a + 2) + 1C2. 分解因式:x2(x - 2) - 16(x - 2) = _________________.(x - 2)(x - 4)(x + 4)3. 已知a + b = 3,a – b = 5,则代数式a2 - b2的值是____.154. 先因式分解,然后计算求值.解:9x2 + 12xy + 4y2 = (3x)2+12xy + (2y)2 = (3x + 2y)2,原式= 9.= ab.5. 利用因式分解计算. (1)32014-32013;(2)(-2)101+(-2)100+299.解(1)32014 - 32013 = 32013×(3 - 1) = 2×32013;(2)(-2)101 + (-2)100+299 = -299(22-2-1)= -299. 6.如图,某农场修建一座小型水库,需要一种空心混凝土管道,它的规格是内径 d = 45 cm,外径 D =75 cm,长 l =300 cm.利用因式分解计算浇制一节这样的管道约需多少立方米的混凝土(π取3.14,结果精确到0.01 m3).当d=45 cm,D=75 cm,l=300 cm时,体积 = 847 800(cm3) ≈ 0.85(m3).
北师版 八年级下册本章章末复习因式分解的定义 把一个多项式化成_____________的形式,这种变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.几个整式的积因式分解与整式乘法的关系因式分解整式乘法因式分解与整式乘法为互逆变形因式分解的方法1.提公因式法 如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法.提公因式法的依据:____________________________.am + bm + cm = m(a + b + c)怎么确定公因式? 各项系数的最大公约数与各项相同字母(或因式)的最低次幂的积.2.公式法 (1) 平方差公式:a2 - b2 = (a + b)(a - b).即两个数的平方差,等于这两个数的和与这个数的差的积. (2)完全平方公式:a2±2ab + b2 = (a±b)2.其中,a2±2ab + b2 叫做完全平方式.思想方法归纳1.整体思想 如果将两个多项式相乘展开后项数太多,而两个多项式中又有相同部分,我们可以考虑将这一部分当成一个整体.因式分解: (x - 2)(x - 4)(x - 6)(x - 8) + 16.解: (x - 2)(x - 4)(x - 6)(x - 8) + 16= [(x - 2) (x - 8)][(x - 4)(x - 6)] + 16= [(x2 -10x) + 16][(x2 - 10x) + 24] + 16= (x2 - 10x)2 + 40(x2 - 10x) + 16×24 + 16= (x2 - 10x)2 + 40(x2 - 10x) + 202= (x2 - 10x + 20)2.2.转化思想 某些多项式从表面上看是无法利用因式分解的一般步骤进行的,需要通过适当的转化,如经过添“-”号、去括号、合并同类项等变形,才能利用因式分解的有关方法进行.把多项式 6x(x - y)2 + 3(y - x)3 因式分解.解:6x(x - y)2 + 3(y - x)3 = 6x(x - y)2 - 3(x - y)3 = 3(x - y)2[2x - (x - y)] = 3(x - y)2(x + y).3.换元思想 换元思想就是将较复杂的式子中的某些整体用新的字母代替,从而使计算简单化.多项式 (x2 + y2) (x2 - 2xy + y2) + x2y2 因式分解.解:设x2 + y2 = m,xy = n.则(x2 + y2) (x2 - 2xy + y2) + x2y2= m(m - 2n) + n2= m2 - 2mn + n2= (m-n)2 = (x2 + y2 - xy)2. 随堂练习将下列多项式因式分解,结果中不含有因 式a + 1的是( ). A. a2 - 1 B. a2 + a C. a2 + a - 2 D. (a + 2)2 - 2(a + 2) + 1C2. 分解因式:x2(x - 2) - 16(x - 2) = _________________.(x - 2)(x - 4)(x + 4)3. 已知a + b = 3,a – b = 5,则代数式a2 - b2的值是____.154. 先因式分解,然后计算求值.解:9x2 + 12xy + 4y2 = (3x)2+12xy + (2y)2 = (3x + 2y)2,原式= 9.= ab.5. 利用因式分解计算. (1)32014-32013;(2)(-2)101+(-2)100+299.解(1)32014 - 32013 = 32013×(3 - 1) = 2×32013;(2)(-2)101 + (-2)100+299 = -299(22-2-1)= -299. 6.如图,某农场修建一座小型水库,需要一种空心混凝土管道,它的规格是内径 d = 45 cm,外径 D =75 cm,长 l =300 cm.利用因式分解计算浇制一节这样的管道约需多少立方米的混凝土(π取3.14,结果精确到0.01 m3).当d=45 cm,D=75 cm,l=300 cm时,体积 = 847 800(cm3) ≈ 0.85(m3).
相关资料
更多










