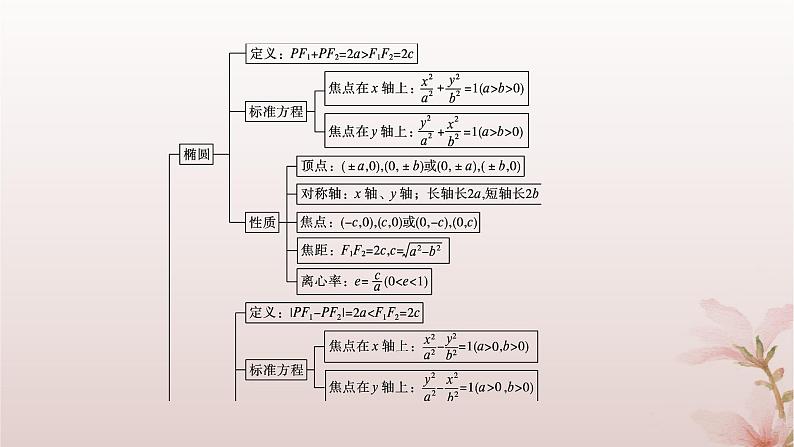
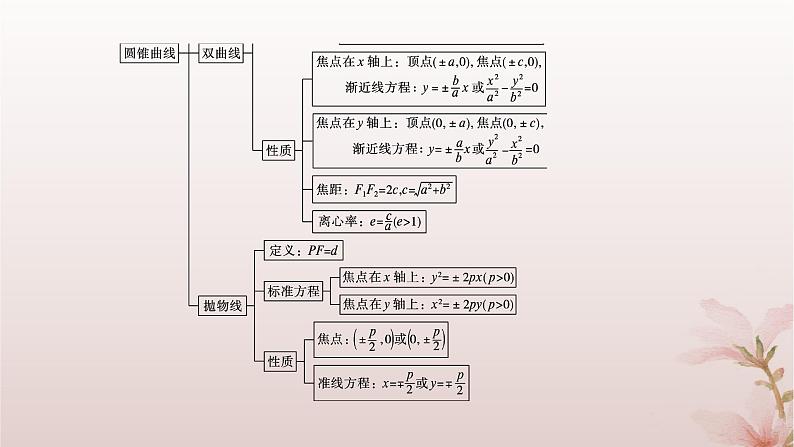
江苏专版2023_2024学年新教材高中数学第3章圆锥曲线与方程章末总结提升课件苏教版选择性必修第一册

这是一份江苏专版2023_2024学年新教材高中数学第3章圆锥曲线与方程章末总结提升课件苏教版选择性必修第一册，共37页。

1网络构建·知识导图2要点归纳·典例提升01网络构建·知识导图02要点归纳·典例提升要点一 圆锥曲线的定义与标准方程 1.求圆锥曲线方程的常用方法  （2）定义法：动点满足已知曲线的定义，可先设定方程，再确定其中的基本量. （3）相关点法：动点满足的条件不便用等式列出，但动点是随着另一动点（称之为相关点）而运动的.如果相关点所满足的条件是明显的，或是可分析的，这时我们可以用动点坐标表示相关点的坐标，根据相关点所满足的方程即可求得动点的轨迹方程. （4）待定系数法：根据条件能确定曲线的类型，可设出方程形式，再根据条件确定待定的系数. 2.求圆锥曲线方程体现了逻辑推理和数学运算、直观想象的数学素养.     题后反思 （1）应用定义解题时注意圆锥曲线定义中的限制条件. （2）涉及椭圆、双曲线上的点与两个定点构成的三角形问题时，常用定义结合解三角形的知识来解决. （3）在求有关抛物线的最值问题时，常利用定义把到焦点的距离转化为到准线的距离，结合几何图形，利用几何意义去解决. D   C   4  要点二 圆锥曲线的几何性质 1.本类问题主要有两种考查类型： （1）已知圆锥曲线的方程研究其几何性质，其中以求椭圆、双曲线的离心率为考查重点. （2）已知圆锥曲线的性质求其方程，基本方法是待定系数法，其步骤可以概括为“先定位、后定量”. 2.圆锥曲线的性质的讨论和应用充分体现了直观想象和逻辑推理的数学素养. AC  图1  图2 B [解析] 如图，    AB  要点三 直线与圆锥曲线的位置关系  2.借用直线与圆锥曲线问题培养数学运算的核心素养.       题后反思 直线与圆锥曲线的位置关系的运用常常用到“设而不求”思想，“设而不求”是解析几何解题的基本手段,是比较特殊的一种思想方法,其实质是整体结构意义上的变式和整体思想的应用.“设而不求”的灵魂是通过科学的手段使运算量最大限度地减少,通过设出相应的参数,利用题设条件加以巧妙转化,以参数为过渡,设而不求.      要点四 圆锥曲线的综合问题 1.圆锥曲线的综合问题包括位置关系证明及定点、定值、最值、探索性问题，解决的基本思路是利用代数法，通过直线与圆锥曲线的方程求解. 2.圆锥曲线的综合问题的解决培养学生的逻辑推理和数学运算素养.      规律方法 圆锥曲线中的定值问题的常见类型及解题策略 （1）求代数式为定值.依题意设条件,得出与代数式参数有关的等式,代入代数式，化简即可得出定值. （2）求点到直线的距离为定值.利用点到直线的距离公式得出距离的解析式,再利用题设条件化简、变形求得. （3）求某线段长度为定值.利用两点间距离公式求得解析式,再根据条件对解析式进行化简、变形即可求得.