






初中数学鲁教版 (五四制)六年级下册3 同底数幂的除法教课ppt课件
展开1、探索学习同底数幂的除法的性质(重点)2、理解并掌握同底数幂的除法的性质。正确运用同底数幂的除法的性质计算(重难点)3、理解并掌握零指数幂和负指数幂公式并能运用熟练运用(重难点)
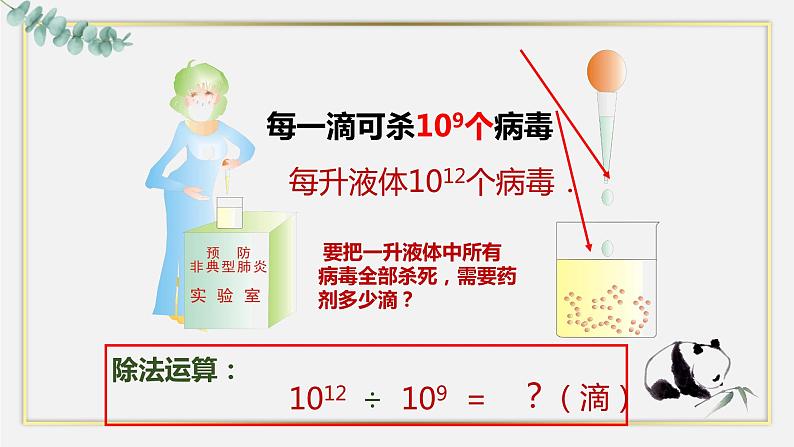
2003年在广州地区流行的“非典型肺炎”,经专家的研究,发现是由一种“病毒”引起的,现有一瓶含有该病毒的液体,其中每升含有1012个病毒. 医学专家进行了实验,发现一种药物对它有特殊的杀灭作用,每一滴这种药物,可以杀死109个病毒. 要把一升液体中的所有病毒全部杀死,需要这种药剂多少滴?
1012 ÷ 109 =
计算下列各式,并说明理由(m>n)
(1) 10 ÷10 =
(2) 10 ÷10 =
(3) (-3) ÷(-3) =
解:(根据幂的定义)
(1) 108 ÷ 105 =
(2) 10m ÷ 10 n =
(3) (-3)m ÷ (-3)n =
同底数幂的除法的一般规律
am ÷ a n =
am ÷a n = (a ≠ 0,m,n都是正整数,且m>n)
同底数幂相除,底数 ,指数 .
105÷ 103﹦____ (- 3)4÷(-3)2﹦____ a6÷ a2=_____
a7-4 = a3
(-x)6-3 = (-x)3 = -x3
(xy)4-1 = (xy)3 = x3y3
b2m+2-2 = b2m
同底数幂相除,底数 ,指数 .
(1) a6 ÷ a1 = a(2)b6 ÷ b3 = b2(3) a10 ÷a9 = a(4)(-bc )4÷ (-bc ) 2 = -b 2 c 2
错误,应等于a6-1 = a5
错误,应等于b6-3 = b3
错误,应等于(-bc )4-2= (-bc ) 2 = b 2 c 2
213-7 = 25 = 32
(-x)7-1 =(-x)6 = x6
(-ab)5-2= (-ab)3 = -a3b3
62m+1-m= 6m+1
计算:
(1)(a-b)7 ÷ (b-a)3 = (2)m19 ÷ m14 ╳ m3 ÷ m =(3) (b2 ) 3 ╳(-b 3)4 ÷(b 5)3 = (4) 98 ╳ 27 2 ÷ (-3) 18 =
=a15 ×a2 ÷a4=a17 ÷a4=a17-4=a13
=x6.x5÷x6=x6+5÷x6=x11÷x6=x11-6=x5
1.已知xm=3,xn=6则x m-n的值。
原式=xm÷xn =3÷6 ﹦1/2
2.若xm=3,xn= 9,求x2m-n的值。
原式=(xm)2÷xn=1
3.已知3m=6, 3n=2,求3 2m-3n的值
3 2m-3n=(3m)2÷(3n)3=9/2
4.已知16m÷8m-1×2m=512求m的值
24m÷23m-3×2m=29 ∴22m+3=29 ∴m=3
x6 ÷x5×1/x5(x-y)7 ÷ (x-y)3×(y-x)2X2m-1 ÷ xm-110a=200,10b=1/5,试求4a ÷22b﹖
am÷an=am-n(a≠0,m,n都是正整数,并且m>n).
一般地,am中指数m可以是零和负整数吗?如果可以,那么a0和负整数指数幂am分别表示什么?
a0=1 (a≠0)
这就是说,任何不等于0的数的0次幂都等于1.
a m÷a n = a m-n 这条性质对于m,n是任意整数的情形仍然适用.
(1) (2)
例2 下列等式是否正确?为什么?(1)am÷an=am·a-n;(2)
解:(1)∵am÷an=am-n=am+(-n)=am·a-n,∴am÷an=am·a-n.故等式正确. (2)
1.填空:(-3)2·(-3)-2=( );103×10-2=( );a-2÷a3=( );a3÷a-4=( ).2.计算:(1)0.1÷0.13(2)(-5)2 014÷(-5)2 016(3)100×10-1÷10-2(4)x-2·x-3÷x2
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少?如果有m个0呢?
类似地,我们可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成a×10-n的形式,其中n是正整数,1≤∣a∣<10.
例3 纳米(nm)是非常小的长度单位,1 nm=10–9 m,把1 nm的物体放到乒乓球上,就如同把乒乓球放到地球上,1 mm3的空间可以放多少个1 nm3的物体?(物体之间间隙忽略不计)
【解析】 1 mm=10-3 m,1 nm=10-9 m.(10-3)3÷ (10-9)3 = 10-9 ÷ 10-27= 1018,1 mm3的空间可以放1018个1 nm3的物体.
0.005 = 5 × 10-3
例4 用科学记数法表示下列各数:
0.02 04
0.020 4=2.04×10-2
(3)0.000 36
0.000 36
0.000 36=3.6×10-4
1.用科学记数法表示:(1)0.000 03; (2)-0.000 006 4;(3)0.000 0314; 2.用科学记数法填空:(1)1 s是1 μs的1 000 000倍,则1 μs=______s;(2)1 mg=______kg;(3)1 μm =______m; (4)1 nm=______ μm ;(5)1 cm2=______ m2 ;(6)1 mL =______m3.
(1)(2×10-6)× (3.2×103)= (2)(2×10-6)2 ÷ (10-4)3 =
4.下列是用科学记数法表示的数,写出原来的数.(1)2×10-8 (2)7.001×10-6答案:(1)0.000 000 02 (2)0.000 007 001
5.比较大小:(1)3.01×10-4________9.5×10-3(2)3.01×10-4________3.10×10-4
1.(益阳·中考)下列计算正确的是( )A.30=0 B.-|-3|=-3C.3-1=-3 D. 32 =±3【解析】选B.30=1,3-1= 32 =3.
2.(聊城·中考)下列计算不正确的是( )A. B.C. D.
3.(怀化·中考)若0
5.某种大肠杆菌的半径是3.5×10-6 m,一只苍蝇携带这种细菌1.4×103个.如果把这种细菌近似地看成球状,那么这只苍蝇所携带的所有大肠杆菌的总体积是多少立方米?(结果精确到0.001,球的体积公式V= πR3)【解析】每个大肠杆菌的体积是 ·π·(3.5×10-6)3≈1.796×10-16( m3),总体积=1.796×10-16×1.4×103≈2.514×10-13( m3).答:这只苍蝇共携带大肠杆菌的总体积是2.514×10-13 m3.
1.零指数幂:当a≠0时,a0=1.2.负整数指数幂:当n是正整数时,a-n=3.整数指数幂的运算性质:(1)am·an=am+n(m,n为整数,a≠0)(2)(ab)m=ambm(m为整数,a≠0,b≠0)(3)(am)n=amn(m,n为整数,a≠0)
北师大版七年级下册3 同底数幂的除法多媒体教学ppt课件: 这是一份北师大版七年级下册3 同底数幂的除法多媒体教学ppt课件,共17页。PPT课件主要包含了温故知新问题探讨,例题解析巩固练习,深入探究稳步提高,小结与作业等内容,欢迎下载使用。
鲁教版 (五四制)六年级下册3 同底数幂的除法教课内容课件ppt: 这是一份鲁教版 (五四制)六年级下册3 同底数幂的除法教课内容课件ppt,共14页。PPT课件主要包含了知识回顾,幂的乘方法则,积的乘方法则,3同底数幂的除法,引入新课,学习目标,预习诊断,规律探究,同底数幂的除法法则,规律应用等内容,欢迎下载使用。
数学八年级上册1.3.1同底数幂的除法试讲课课件ppt: 这是一份数学八年级上册1.3.1同底数幂的除法试讲课课件ppt,文件包含湘教版8上数学第一章13《同底数幂除法》课件pptx、湘教版8上数学第一章13《同底数幂的除法》教案docx等2份课件配套教学资源,其中PPT共21页, 欢迎下载使用。













