数学五年级上册实际问题与方程教案设计

这是一份数学五年级上册实际问题与方程教案设计，共11页。
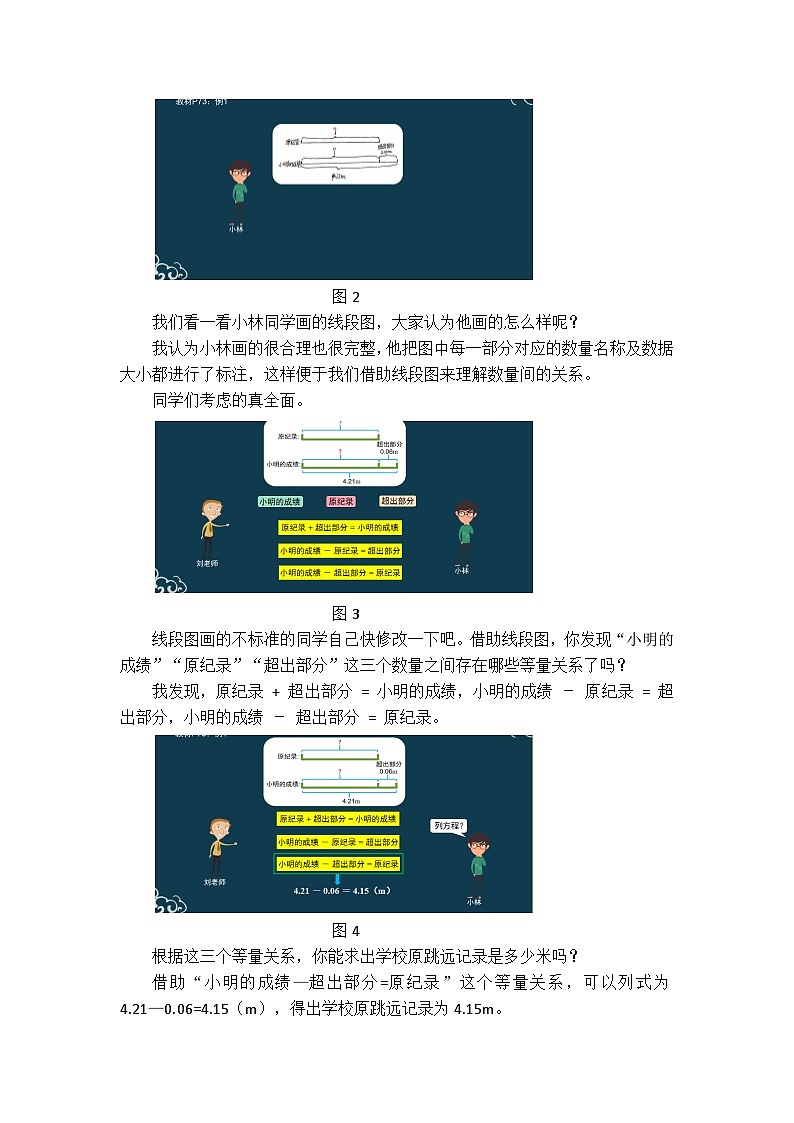
实际问题与方程（一）      [课程内容] 人教版五年级上册 第73—76页 例1、例2及练习十六。[教学目标]1.能根据具体问题找出等量关系，列出方程，并正确解答。2.感受数学与生活的联系，能根据实际情况灵活选择算法，初步学会列方程解决一些简单的实际问题，培养学生解决问题的能力。3.培养学生的数学应用意识，养成规范书写、自觉检查的习惯。[教学重点、难点]感受数学与生活的联系，能根据实际情况灵活选择算法，初步学会列方程解决一些简单的实际问题，培养学生解决问题的能力。 [脚本正文]同学们，大家好。今天我们一起来学习人教版小学数学五年级上册第五单元的第八课时--实际问题与方程（一）。 一、自主探索，学习新知     图1同学们，你们看，小明正在参加学校举行的秋季运动会，他打破了学校的跳远记录。从图中你能找到哪些数学信息？小林你来说一说吧。从图中我们能得知，小明的成绩为4.21m，超过原纪录0.06m，要求学校原跳远记录是多少米？怎样理解题目中“超过原纪录0.06m”这个数学信息呢？这个数学信息告诉我们小明的成绩比原纪录多0.06m或原纪录比小明的成绩少0.06m。这三个数量之间有什么关系呢？有什么好的方法能帮助我们进行分析呢？可以画线段图来理解它们之间的关系。那同学们就试着画一画吧。大家画完了吗？     图2我们看一看小林同学画的线段图，大家认为他画的怎么样呢？我认为小林画的很合理也很完整，他把图中每一部分对应的数量名称及数据大小都进行了标注，这样便于我们借助线段图来理解数量间的关系。同学们考虑的真全面。        图3线段图画的不标准的同学自己快修改一下吧。借助线段图，你发现“小明的成绩”“原纪录”“超出部分”这三个数量之间存在哪些等量关系了吗？我发现，原纪录 + 超出部分 = 小明的成绩，小明的成绩 － 原纪录 = 超出部分，小明的成绩 － 超出部分 = 原纪录。     图4根据这三个等量关系，你能求出学校原跳远记录是多少米吗？借助“小明的成绩—超出部分=原纪录”这个等量关系，可以列式为4.21—0.06=4.15（m），得出学校原跳远记录为4.15m。大家还有其他的解题方法吗？我们能不能列方程来解决呢？那怎样来列方程解决呢？图5请大家打开书73页，先自学例1这一部分内容，然后再试着列方程进行解答。给大家一些时间，动手开始吧。大家完成了吗？     图6我们先让小林说一说，他是如何列方程进行解答的。通过自学，我发现：在列方程解答问题时，我们要先写一个“解”字，再把要求的数量也就是未知数设为x。在这个问题中，原纪录是未知数，所以我们应这样书写“解：设学校原跳远记录是x m。”需要注意的是，在设未知数时，x后面要写上单位。接着，我们列出方程，根据等量关系“原纪录+超出部分=小明的成绩”，可以列出方程：x+0.06=4.21，根据等式的性质1进行解方程，得出x=4.15，需要注意的是我们在设未知数时，已经标明了单位“m”，所以在解方程过程中，方程的解后面不需要再写单位。最后，我们再写上答话，答：学校原跳远记录是4.15m。小林讲得可真细致，同学们，你都学会了吗？     图7下面，我们再看一看小丽是如何列方程解答的。先“解：设学校原跳远记录是x m。”我根据“小明的成绩—原纪录=超出部分”这个等量关系，列出方程:4.21—x=0.06，根据等式的性质1，左右两边先加上x，最后得出x=4.15，学校原跳远记录是4.15 m。     图8这两位同学求得的解正确吗？我们可以怎样检验呢？可以将x=4.15分别代入方程进行检验。除了代入方程检验，还可以怎样检验呢？还可以将结果代入题目中，结合题目中的关键信息进行检验。这样检验，可以确信我们的解答是正确的。同学们想一想，当我们列方程解决实际问题时应该注意些什么呢？应该先写“解”字，设未知数为x；再根据题目中的等量关系列出方程、解答并写出答话；在设未知数为x时，后面要写单位，方程的解后面不用写单位；最后记得要检验。那这两个方程，大家更喜欢列出哪一个呢？我们更喜欢列出第一个。为什么呢？因为顺应题目中的关键信息“小明的成绩超过原纪录0.06m”去思考，我们能够快速的找出等量关系并列出方程进行解答。有关列方程解决实际问题大家都学会了吗？     图9现在，试着自己独立列方程解决这个问题。大家完成了吗？     图10小林说说你是怎样做的吧。顺应题目中的信息，我发现了“去年身高＋长高部分=今年身高”这一等量关系。在解答时，先将题目中的数量单位都统一为米，8cm=0.08m，解：设小明去年身高为xm，根据等量关系列方程为0.08+x=1.53，求出x=1.45，小明去年身高为1.45m。     图11我们再来看看，小雪的解答过程。通过画图分析，我还发现了“今年身高—去年身高=长高部分”，可以列方程为1.53—x=0.08，在解方程时，根据等式的性质1，左右两边要先加x，最后也得出x=1.45，小明去年身高为1.45m。同学们真棒，能够准确找出题目中的等量关系，确保我们正确列出方程。     图12同学们，你了解足球的构成吗？一个足球上黑色的皮都是五边形的，白色的皮都是六边形的，白色皮共有20块，比黑色皮的2倍少4块，那一共有多少块黑色皮呢？怎样理解“白色皮共有20块，比黑色皮的2倍少4块”呢？你能根据这个关键信息列出方程并进行解答吗？大家开始吧。     图13小林你说说你是怎样列方程解答的。顺应题目中的关键信息，我发现了“黑色皮块数×2－4＝白色皮块数”，根据这个等量关系，列方程为2x－4=20，解方程时将“2x”看作一个整体，先求出2x=24，再求出x=12，所以共有12块黑色皮。小林讲的真棒，想一想我们还可以列出其它方程解答吗？大家试着写一写吧。     图14我们先看看小丽的解答过程。通过画图分析，我发现了“黑色皮块数×2－白色皮块数＝4”，可以列方程为2x－20=4，解方程时依然把“2x”看作一个整体，求出x=12，共有12块黑色皮。     图15我们再看看小雪的解答过程。通过画图分析，我还发现“黑色皮块数×2＝白色皮块数＋4”，可以列方程为2x=20+4，求出x=12，共有12块黑色皮。图16三位同学求得的解正确吗？大家检验了吗？通过将结果代入题目检验，我们的解答是正确的。那以上三个方程，大家更喜欢列出哪一个呢？我们更喜欢列出第一个。为什么呢？因为顺应题目中的关键信息进行分析，便于我们思考并能够快速的找出等量关系、列出方程。     图17回顾刚才的解答过程，在列方程解决实际问题时都有哪些步骤呢？通过阅读题目信息，我们要先找出未知数，用字母x表示；然后分析实际问题中的数量关系，找出等量关系，列方程；最后解方程并检验作答。大家认为在列方程解决实际问题时，哪一步最关键呢？我们认为第二步最关键。怎样才能快速、准确的找出等量关系呢？我们应该顺应题目中的关键数学信息去理解与分析，找出等量关系。接下来我们一起列方程来解决生活中的其他实际问题。二、巩固练习，思维提升     图18长江是我国的第一长河，长6299km，比黄河长835km，那黄河长多少千米呢？你能根据关键数学信息列方程解答这个问题吗？根据题目中的关键数学信息，我发现了“黄河的长度＋835=长江的长度”。解：设黄河长x千米，根据等量关系列方程为x+835=6299，求出x=5464。所以黄河长5464千米。其他同学，你们都做对了吗？     图19故宫和天安门广场，大家都去游玩过吗？已知故宫的面积是72万平方米，比天安门广场面积的2倍少16万平方米。那天安门广场的面积是多少万平方米？大家找出这个题目中的关键数学信息了吗？关键数学信息是“故宫的面积比天安门广场面积的2倍少16万平方米”现在你能根据这个关键信息进行列方程解答吗？大家开始吧。根据题目中的关键信息进行分析，我发现“天安门广场的面积×2－16=故宫的面积”。解：设天安门广场的面积为x万平方米，根据等量关系列方程为2x－16=72，在解方程时先将2x看作一个整体，先求出2x=88，再求出x=44。所以，天安门广场的面积为44万平方米。     图20大家知道我们的祖国位于世界上的哪个大洲吗？对，位于亚洲。世界上最大的洲是亚洲，面积是4400万平方千米。最小的洲是大洋洲，亚洲的面积比大洋洲面积的4倍还多812万平方千米。那大洋洲的面积是多少万平方千米？这个题目中的关键数学信息大家找到了吗？关键数学信息是“亚洲的面积比大洋洲面积的4倍还多812万平方千米”大家能根据这个关键信息快速的列出方程进行解答吗？解：设大洋洲的面积为x万平方千米，顺应题目中的关键信息，我们能快速的找出“大洋洲的面积×4+812=亚洲的面积”这一等量关系，列出方程4x+812=4400，在解方程时先将4x看作一个整体，先求出4x=3588，再求出x=897。所以，大洋洲的面积为897万平方千米。   三、自主梳理，内化提升     图21通过本节课的学习，大家都有哪些收获呢？自己梳理一下吧。本节课我们学习了列方程来解决生活中的实际问题，要经历以下3个步骤。我们还体会到，顺应题目中的关键数学信息能够快速找准问题中的等量关系，正确列出方程。看来，通过本节课的学习，同学们都有着非常丰富的收获。     图22课下，同学们来完成这几道习题，并把自己的学习收获分享给自己的爸爸和妈妈吧。今天的学习就到这里，期待在下节课中大家会有更加精彩的表现，同学们再见。