


高中物理人教版(2019)必修第一册 第3章 相互作用章末总结教案
展开第三章相互作用章末总结
一、 教材分析
本章在物理知识方面可分为两部分:第一部分是1节至3节,主要讲述了重力、重力产生的原因、重心、力、力的三要素、力的效果、四种基本相互作用、弹力产生的条件、弹力、压力、支持力、拉力、力的图示、力的示意图、形变、胡克定律、静摩擦力、静摩擦力产生的条件、滑动摩擦力、滑动摩擦力产生的条件、最大静摩擦力、滚动摩擦力、流体阻力、滑动摩擦力跟压力成正比。第二部分是4节至5节,主要讲述了力的平行四边形定则、力的合成、合力、分力、共点力、作图法求力、用直角三角形知识求力、力的分解、矢量、标量、三角形定则、共点力的平衡等概念。
在物理技能方面,主要设计及使用了弹簧秤、初步训练设计实验、收集数据、数据处理和总结规律的技能、运用数学工具解决物理问题的能力等基本技能。
在物理过程方面,主要讲述了人类是从力产生的效果开始认识力、“重心”概念的形成、微小形变的放大过程、摩擦力的实验探究、实验探究互成角度的两个共点力的合成等过程。
在物理的思想方法方面,主要讲述了等效代换、微小量放大的方法、控制变量、客观求实的科学研究态度等思想方法。
二、 教学目标
1、通过实验认识滑动摩擦、静摩擦的规律,能用动摩擦因数计算摩擦力。
2、知道常见的形变,通过实验了解物体的弹性,知道胡克定律
3、通过实验,理解力的合成与分解,知道共点力的平衡条件,区分矢量和标量,用力的合成与分解分析日常生活中的问题
三、 教学重点
三种性质力――重力、弹力、摩擦力;力的合成与分解。
四、 教学难点
用力的合成与分解分析解决实际问题。
五、 教学过程
(一)投影全章知识脉络,构建知识体系
(二)本章复习思路突破
Ⅰ 物理思维方法
l、具体——抽象思维方法
从大量生活实例中抽象出“力是物体间的相互作用”,再把这种抽象具体形象化――用有向线段进行描述,通过这种方法,把对力的计算转化为几何问题来处理。
2、等效替代方法
合力和分力可以等效替代,而不改变其作用效果。这是物理学中研究实际问题时常用的方法。
Ⅱ 基本解题思路
1、认清研究对象:从题目所给的信息来选取有关物体作为研究对象,是解题的出发点。
2、正确受力分析:分析研究对象受哪些力的作用,画出受力图,做到不多力,不少力。
3、列方程求解:据物理规律先用字母列方程,整理出待求量的表达式,统一单位,代入数据求解。
(三)知识要点追踪
关于受力分析
物体受力分析是力学知识中的基础,也是其重要内容。正确分析物体的受力情况,是研究力学问题的关键,是必须掌握的基本功。
对物体进行受力分析,主要依据力的概念,分析物体所受到的其他物体的作用。具体方法如下:
1、明确研究对象,即首先要确定要分析哪个物体的受力情况。
2、隔离分析:将研究对象从周围环境中隔离出来,分析周围物体对它都施加了哪些作用。
3、按一定顺序分析:先重力,后接触力(弹力、摩擦力)。其中重力是非接触力,容易遗漏,应先分析;弹力和摩擦力的有无要依据其产生的条件认真分析。
4、画好受力分析图。要按顺序检查受力分析是否全面,做到不“多力”也不“少力”。
(四)本章专题剖析
[例1]如图所示,物体受到互相垂直的两个力F1、F2的作用,若两力大小分别为5![]() N、5N,求这两个力的合力.
N、5N,求这两个力的合力.
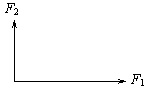
解析:根据平行四边形定则作出平行四边形,如图所示,由于F1、F2相互垂直,所以作出的平行四边形为矩形,对角线分成的两个三角形为直角三角形,由勾股定理得:
![]() N=10 N
N=10 N
合力的方向与F1的夹角θ为:
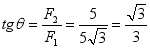 θ=30°
θ=30°
点评:今后我们遇到的求合力的问题,多数都用计算法,即根据平行四边形定则作出平行四边形后,通过解其中的三角形求合力.在这种情况下作的是示意图,不需要很严格,但要规范,明确哪些该画实线,哪些该画虚线,箭头应标在什么位置等.
[例2]如左图所示,物体受到大小相等的两个拉力的作用,每个拉力均为200 N,两力之间的夹角为60°,求这两个拉力的合力。
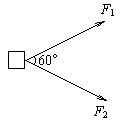
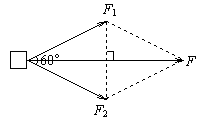
解析:根据平行四边形定则,作出示意图(如右图所示),它是一个菱形,我们可以利用其对角线垂直平分,通过解其中的直角三角形求合力.
![]() N=346 N
N=346 N
合力与F1、F2的夹角均为30°.
小结:(1)求矢量时要注意不仅要求出其大小,还要求出其方向,其方向通常用它与已知矢量的夹角表示.
(2)要学好物理,除掌握物理概念和规律外,还要注意提高自己应用数学知识解决物理问题的能力.
[例3]如图(甲),半圆形支架BAO,两细绳OA与OB结于圆心O,下悬重为G的物体,使OA绳固定不动,在将OB绳的B端沿半圆支架从水平位置逐渐移至竖直的位置C的过程中,分析OA绳与OB绳所受力的大小如何变化?
解析: 因为绳结O受到重物的拉力T,所以才使OA绳和OB绳受力,因此将拉力T分解为![]() 和
和![]() ,如图(乙),OA绳固定,则
,如图(乙),OA绳固定,则![]() 的方向不变,在OB绳向上靠近OC的过程中,在
的方向不变,在OB绳向上靠近OC的过程中,在![]() 、
、![]() 、
、![]() 三个位置,两绳受的力分别为
三个位置,两绳受的力分别为![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,从图形上看出
,从图形上看出![]() 一直减小,而
一直减小,而![]() 却是先变小后增大,当OB与OA垂直时
却是先变小后增大,当OB与OA垂直时![]() 最小.
最小.
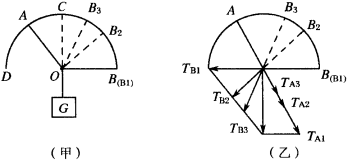
点评:(1)这类平衡问题,是一个物体受到三个力(或可等效为三个力)而平衡,其中一个力的大小和方向是确定的(如重力)而另一个力的方向始终不变,第三个力的大小和方向都可改变.问第三个力取什么方向这个力有最小值.当第三个力的方向跟第二个力垂直时,有最小值,这一规律搞清楚后,运用作图法或计算法就比较方便了。
(2)通过平行四边形的邻边和对角线长短关系或变化情况,做一些较为复杂的定性分析,从图上就可以看出结果,得出结论。这种方法称为图解法。
(五)课堂练习
1、将一个力F分解为不为零的两个分力,下列哪些分解结果是不可能的
A.分力之一垂直于F B.两个分力都在同一条直线上
C.一个分力的大小与F的大小相等 D.一个分力与F相等
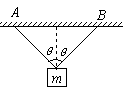
2、两根长度相等的轻绳,下端悬挂一质量为m的物体,上端分别固定于天花板上的A、B两点,已知两绳所能经受的最大拉力均为FT,则每根轻绳的长度不得短于多少?
3、质量为2 kg的物体放在水平地板上,用一轻弹簧水平拉该物体,当物体刚开始运动时,弹簧伸长了3 cm,当拉着物体前进时,弹簧伸长2 cm,已知弹簧的劲度系数为k= 200 N/m(g=10 N/kg),求:
(1)物体所受的最大静摩擦力为多少?
(2)物体和地板间的动摩擦因数
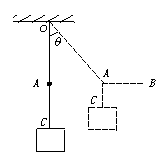
4、如图所示,物重30 N,用OC绳悬挂在O点,OC绳能承受最大拉力为20![]() N,再用一绳系OC绳的A点,BA绳能承受的最大拉力为30 N,现用水平力拉BA,可以把OA绳拉到与竖直方向成多大角度?
N,再用一绳系OC绳的A点,BA绳能承受的最大拉力为30 N,现用水平力拉BA,可以把OA绳拉到与竖直方向成多大角度?
参考答案:
1、D
2、l≥
3、解析:(1)根据胡克定律,F=k x,当弹簧伸长3 cm时,弹簧的拉力为6 N;弹簧伸长2 cm时,弹簧的拉力为4 N.再由平衡的知识,可得物体所受的最大静摩擦力为6 N.
(2)滑动摩擦力为Ff=4 N,正压力FN=G=20 N,所以动摩擦因数μ=Ff/FN=0.2
4、解析:当OA绳与竖直方向的夹角θ逐渐增大时,OA和BA绳中的拉力都逐渐增大.其中某一根的拉力达到它本身能承受的最大拉力时,就不能再增大角度了.显然,OA绳中的拉力先达到这一要求.
所以有cosθ=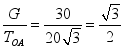
所以θ=30°
六、 课堂小结









