


江苏省苏州吴中学区2022-2023学年数学七下期末预测试题含答案
展开江苏省苏州吴中学区2022-2023学年数学七下期末预测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若A(x1,y1)、B(x2,y2)是一次函数y=ax+x-2图像上的不同的两点,记![]() ,则当m<0时,a的取值范围是( )
,则当m<0时,a的取值范围是( )
A.a<0 B.a>0 C.a<-1 D.a>-1
2.已知平行四边形的一边长为10,则对角线的长度可能取下列数组中的( ).
A.4、8 B.10、32 C.8、10 D.11、13
3.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①BE=DF;②∠AEB=75°;③CE=2;④S正方形ABCD=2+![]() ,其中正确答案是( )
,其中正确答案是( )
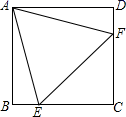
A.①② B.②③ C.①②④ D.①②③
4.使用同一种规格的下列地砖,不能进行平面镶嵌的是( )
A.正三角形地砖 B.正四边形地砖 C.正五边形地砖 D.正六边形地砖
5.如图,在![]() 中,
中,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
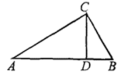
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.公式![]() 表示当重力为P时的物体作用在弹簧上时弹簧的长度.
表示当重力为P时的物体作用在弹簧上时弹簧的长度.![]() 表示弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( )
表示弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( )
A.L=10+0.5P B.L=10+5P C.L=80+0.5P D.L=80+5P
7.以下各点中,在一次函数![]() 的图像上的是( )
的图像上的是( )
A.(2,4) B.(-1,4) C.(0,5) D.(0,6)
8.下列事件中是不可能事件的是( )
A.任意画一个四边形,它的内角和是360°
B.若![]() ,则
,则![]()
C.一只不透明的袋子共装有3个小球,它们的标号分别为1、2、3,从中摸出一个小球,标号是“5”
D.掷一枚质地均匀的硬币,落地时正面朝上
9.下列各式中,运算正确的是( )
A.![]() B.
B.![]()
C.2+![]() =2
=2![]() D.
D.![]()
10.如图,正方形ABCD中,点E在BD上,且![]() ,延长CE交AD于F,则
,延长CE交AD于F,则![]() 为( )
为( )
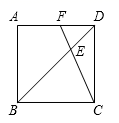
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.使根式![]() 有意义的
有意义的![]() 的范围是( ).
的范围是( ).
A.x≥0 B.x≥4 C.x≥-4 D.x≤-4
12.如图,Rt△ABC中,∠C=90°,AB=10,BC=8,将△ABC折叠,使B点与AC的中点D重合,折痕为EF,则线段BF的长是( )
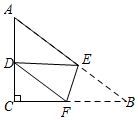
A.![]() B.2 C.
B.2 C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.一个反比例函数![]() (k≠0)的图象经过点P(-2,-1),则该反比例函数的解析式是________.
(k≠0)的图象经过点P(-2,-1),则该反比例函数的解析式是________.
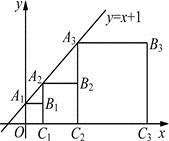
14.正方形![]() ,
,![]() ,
,![]() ,…按如图所示的方式放置.点
,…按如图所示的方式放置.点![]() ,
,![]() ,
,![]() ,…和点
,…和点![]() ,
,![]() ,
,![]() ,…分别在直线
,…分别在直线![]() 和
和![]() 轴上,则点
轴上,则点![]() 的坐标是 .
的坐标是 .
15.若关于x的分式方程![]() 的解为非负数,则a的取值范围是_____.
的解为非负数,则a的取值范围是_____.
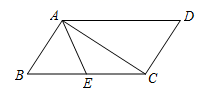
16.如图,平行四边形ABCD中,AC⊥AB,点E为BC边中点,AD=6,则AE的长为________.
17.如图,是用形状、大小完全相同的等腰梯形镶嵌的图案,则这个图案中的等腰三角形的底角(指锐角)的度数是_____.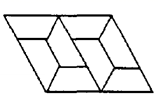
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.
(1)如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接
写出结论;
(2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
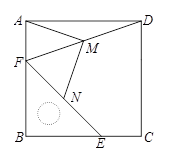
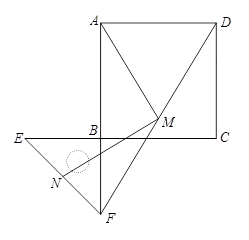
图1 图2
19.(5分)解方程:x2﹣6x+8=1.
20.(8分)菱形ABCD中,∠BAD=60°,BD是对角线,点E、F分别是边AB、AD上两个点,且满足AE=DF,连接BF与DE相交于点G.
(1)如图1,求∠BGD的度数;
(2)如图2,作CH⊥BG于H点,求证:2GH=GB+DG;
(3)在满足(2)的条件下,且点H在菱形内部,若GB=6,CH=4![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
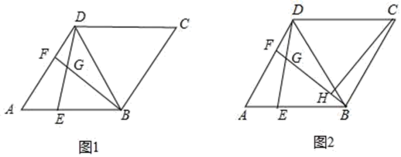
21.(10分)在2019年春季环境整治活动中,某社区计划对面积为![]() 的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为
的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为![]() 区域的绿化时,甲队比乙队少用5天.
区域的绿化时,甲队比乙队少用5天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成绿化任务,求
天,刚好完成绿化任务,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
22.(10分)如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8厘米,AB=6厘米,P从点A出发,以1厘米/秒的速度向D运动(不与D重合).设点P运动时间为t秒,请用t表示PD的长;并求t为何值时,四边形PBQD是菱形.

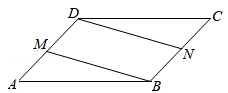
23.(12分)已知:在平行四边形ABCD中,AM=CN.求证:四边形MBND是平行四边形.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、D
3、C
4、C
5、A
6、A
7、D
8、C
9、A
10、B
11、C
12、D
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、(63,32).
15、![]() 且
且![]()
16、1
17、60°
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)MA=MN,MA⊥MN;(2)成立,理由详见解析
19、x1=2 x2=2.
20、(1)∠BGD=120°;(2)见解析;(3)S四边形ABCD=26![]() .
.
21、(1)甲、乙两工程队每天能完成绿化面积分别为![]() 和
和![]() ;(2)
;(2)![]() ;(3)甲工程队施工15天,乙工程队施工10天,则施工总费用最低,最低费用为11.5万.
;(3)甲工程队施工15天,乙工程队施工10天,则施工总费用最低,最低费用为11.5万.
22、(1)证明见解析(2)![]()
23、证明见解析.
江苏省苏州吴中学区2023-2024学年九上数学期末复习检测试题含答案: 这是一份江苏省苏州吴中学区2023-2024学年九上数学期末复习检测试题含答案,共8页。试卷主要包含了答题时请按要求用笔,的绝对值是等内容,欢迎下载使用。
2023-2024学年江苏省苏州市吴中学区统考数学九上期末预测试题含答案: 这是一份2023-2024学年江苏省苏州市吴中学区统考数学九上期末预测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,二次函数的最小值是,如图,四边形内接于,若,则等内容,欢迎下载使用。
江苏省苏州吴中学区2023-2024学年数学九上期末调研试题含答案: 这是一份江苏省苏州吴中学区2023-2024学年数学九上期末调研试题含答案,共8页。












