


天津市两学校2022-2023学年七年级数学第二学期期末统考模拟试题含答案
展开天津市两学校2022-2023学年七年级数学第二学期期末统考模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.以三角形三边中点和三角形三个顶点能画出平行四边形有( )个.
A.1 B.2 C.3 D.4
2.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=( )度.
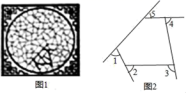
A.270° B.300°
C.360° D.400°
3.如图,在![]() 中,
中,![]() ,
,![]() ,点D是AB的中点,则
,点D是AB的中点,则![]()
![]()
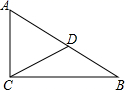
A.4 B.5 C.6 D.8
4.函数![]() 中自变量
中自变量![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.全体实数
D.全体实数
5.如图,剪两张对边平行且宽度相同的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )
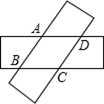
A.∠ABC=∠ADC,∠BAD=∠BCD B.AB=BC
C.AB=CD,AD=BC D.∠DAB+∠BCD=180°
6.若一次函数的![]() 图象上有两点
图象上有两点![]() ,则下列
,则下列![]() 大小关系正确的是( )
大小关系正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.一次函数y=2x﹣1的图象大致是( )
A.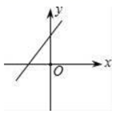 B.
B.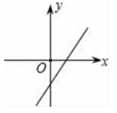 C.
C.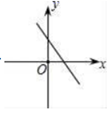 D.
D.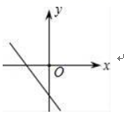
8.如图,菱形![]() 中,
中,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的度数是( )
的度数是( )
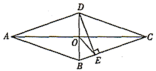
A.35° B.30° C.25° D.20°
9.关于函数y=﹣x+3,下列结论正确的是( )
A.它的图象必经过点(1,1) B.它的图象经过第一、二、三象限
C.它的图象与y轴的交点坐标为(0,3) D.y随x的增大而增大
10.如图,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,则根据图象可知不等式
,则根据图象可知不等式![]() 的解集是
的解集是![]()
![]()
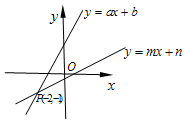
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知函数![]() ,当
,当![]() = _______ 时,直线过原点;
= _______ 时,直线过原点;![]() 为 _______ 数时,函数
为 _______ 数时,函数![]() 随
随![]() 的增大而增大 .
的增大而增大 .
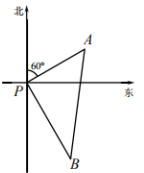
12.如图,某港口P位于南北延伸的海岸线上,东面是大海.“远洋”号、“长峰”号两艘轮船同时离开港口P,各自沿固定方向航行,“远洋”号每小时航行12n mile,“长峰”号每小时航行16n mile,它们离开港东口1小时后,分别到达A,B两个位置,且AB=20n mile,已知“远洋”号沿着北偏东60°方向航行,那么“长峰”号航行的方向是________.
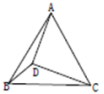
13.如图,点D是等边![]() 内部一点,
内部一点,![]() ,
,![]() ,
,![]() .则
.则![]() 的度数为=________°.
的度数为=________°.
14.已知m是方程x2﹣2018x+1=0的一个根,则代数式m2﹣2017m+![]() +3的值等于_____.
+3的值等于_____.
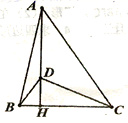
15.如图在△ABC中,AH⊥BC于点H,在AH上取一点D,连接DC,使DA=DC,且∠ADC=2∠DBC,若DH=2,BC=6,则AB=_________________。
16.![]() 的平方根是____.
的平方根是____.
三、解下列各题(本大题共8小题,共72分)
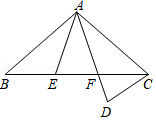
17.(8分)如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC,
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.
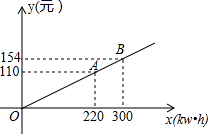
18.(8分)某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过220kW•h时实行“基础电价”;第二档是当用电量超过220kW•h时,其中的220kW•h仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为xkW•h时,应交电费为y元.具体收费情况如图所示,请根据图象回答下列问题:
(1)“基础电价”是 元/kw•h;
(2)求出当x>220时,y与x的函数解析式;
(3)若小豪家六月份缴纳电费121元,求小豪家这个月用电量为多少kW•h?
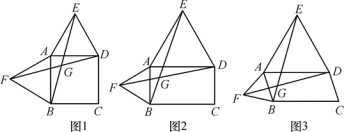
19.(8分)以四边形ABCD的边AB,AD为边分别向外侧作等边△ABF和等边△ADE,连接EB,FD,交点为G.
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由.
20.(8分)在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(公里)与甲车行驶时间(小时)之间的函数关系如图,请根据所给图象关系解答下列问题:
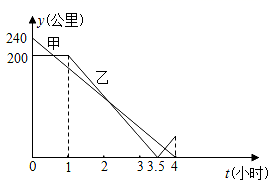
(1)求甲、乙两车的行驶速度;
(2)求乙车出发1.5小时后,两车距离多少公里?
(3)求乙车出发多少小时后,两车相遇?
21.(8分)乙知关于![]() 的方程
的方程![]() .
.
(1)试说明无论![]() 取何值时,方程总有两个不相等的实数很;
取何值时,方程总有两个不相等的实数很;
(2)如果方程有一个根为![]() , 试求
, 试求![]() 的值.
的值.
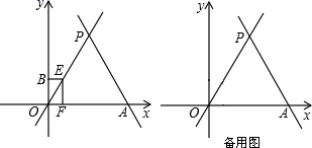
22.(10分)如图,直线![]() 与x轴相交于点A,与直线
与x轴相交于点A,与直线![]() 相交于点P.
相交于点P.
(1)求点P的坐标.
(2)请判断△OPA的形状并说明理由.
(3)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.求S与t之间的函数关系式.
23.(10分)如图,在△ABC中,AB =AC,BD⊥AC,CE⊥AB,求证:BD=CE.
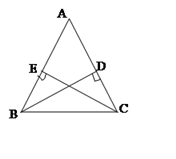
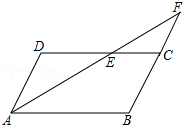
24.(12分)如图,平行四边形ABCD中,![]() ,
,![]() ,AE平分
,AE平分![]() 交BC的延长线于F点,求CF的长.
交BC的延长线于F点,求CF的长.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、C
3、B
4、A
5、D
6、B
7、B
8、C
9、C
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]() m>0
m>0
12、南偏东30°
13、1
14、1
15、![]()
16、±3
三、解下列各题(本大题共8小题,共72分)
17、(1)证明见解析;(2)1.
18、(1)0.5;(2)y=0.55x﹣11;(3)小豪家这个月用电量为1kW•h.
19、(1)EB=FD;(2)EB=FD,证明见解析;(3)∠EGD不发生变化.
20、(1)甲车的行驶速度 60(km/h),乙车的行驶速度80(km/h);(2)两车距离170公里;(3)乙车出发![]() 小时后,两车相遇.
小时后,两车相遇.
21、(1)详见解析;(2)2003
22、(1)![]() ;(2)△POA是等边三角形,理由见解析;(3)当0<t≤4时,
;(2)△POA是等边三角形,理由见解析;(3)当0<t≤4时,![]() ,当4<t<8时,
,当4<t<8时,![]()
23、略
24、![]() .
.
2023-2024学年天津市两学校数学八上期末调研模拟试题含答案: 这是一份2023-2024学年天津市两学校数学八上期末调研模拟试题含答案,共8页。试卷主要包含了在平面直角坐标系中,点P,对于一次函数,下列说法正确的是等内容,欢迎下载使用。
湖北省武汉市两学校2022-2023学年七下数学期末质量跟踪监视模拟试题含答案: 这是一份湖北省武汉市两学校2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,点M,点P,已知下列命题等内容,欢迎下载使用。
天津市第十九中学2022-2023学年数学七年级第二学期期末统考模拟试题含答案: 这是一份天津市第十九中学2022-2023学年数学七年级第二学期期末统考模拟试题含答案,共7页。













