天津市红桥区2022-2023学年七年级数学第二学期期末检测模拟试题含答案

天津市红桥区2022-2023学年七年级数学第二学期期末检测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

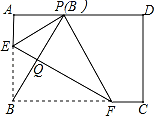
1．如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=3EQ；④△PBF是等边三角形，其中正确的是（　　）

A．①②③ B．②③④ C．①②④ D．①③④

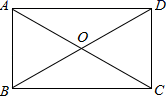
2．矩形ABCD的对角线AC、BD相交于点O，∠AOD＝120°，AC＝8，则△ABO的周长为（　　）

A．12 B．14 C．16 D．18

3．若分式(x≠0，y≠0)中x，y同时扩大3倍，则分式的值（   ）

A．扩大3倍 B．缩小3倍 C．改变 D．不改变

4．函数y=中自变量x的取值范围是（　　）

A．x＞3 B．x＜3 C．x≤3 D．x≥﹣3

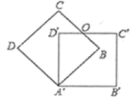
5．把边长为3的正方形绕点A顺时针旋转45°得到正方形，边与交于点O，则四边形的周长是（    ）

A．6 B． C． D．

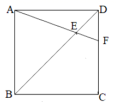
6．如图，正方形中，，连接交对角线于点，那么（  ）

A． B． C． D．

7．电影院里的座位按“×排×号”编排，小明的座位简记为(12，6)，小菲的座位简记为(12，12)，则小明与小菲坐的位置为(    )

A．同一排 B．前后同一条直线上 C．中间隔六个人 D．前后隔六排

8．如图，EF是Rt△ABC的中位线，∠BAC＝90°，AD是斜边BC边上的中线，EF和AD相交于点O，则下列结论不正确的是（　　）

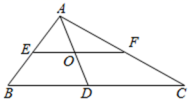
A．AO＝OD B．EF＝AD C．S△AEO＝S△AOF D．S△ABC＝2S△AEF

9．如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是（ ）

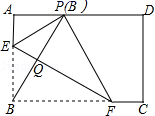
A．①② B．②③ C．①③ D．①④

10．已知平行四边形中，一个内角，那么它的邻角（    ）.

A． B． C． D．

11．如图，在△ABC中，AB=5，BC=6，AC=7，点D，E，F分别是△ABC三边的中点，则△DEF的周长为（    ）

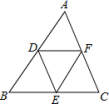
A．12 B．11 C．10 D．9

12．下列四组线段中，可以构成直角三角形的是（    ）

A．1、、 B．2、3、4 C．1、2、3 D．4、5、6

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如图，在矩形中，，．若点是边的中点，连接，过点作交于点，则的长为______．

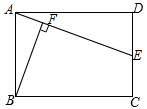
14．如果三角形三边长分别为，k，，则化简得___________．

15．已知矩形的长a＝，宽b＝，则这个矩形的面积是_____．

16．已知a2-2ab+b2=6，则a-b＝_________.

17．若是的小数部分，则的值是______．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）某市政府为了增强城镇居民抵御大病风险的能力，积极完善城镇居民医疗保险制度，纳入医疗保险的居民的大病住院医疗费用的报销比例标准如下表：

设享受医保的某居民一年的大病住院医疗费用为x元，按上述标准报销的金额为y元．

（1）直接写出x≤50000时，y关于x的函数关系式，并注明自变量x的取值范围；

（2）若某居民大病住院医疗费用按标准报销了20000元，问他住院医疗费用是多少元？

19．（5分）（问题原型）如图，在中，对角线的垂直平分线交于点，交于点，交于点.求证：四边形是菱形.

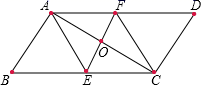
（小海的证法）证明：

是的垂直平分线，

，（第一步）

，（第二步）

.（第三步）

四边形是平行四边形.（第四步）

四边形是菱形.  （第五步）

（老师评析）小海利用对角线互相平分证明了四边形是平行四边形，再利用对角线互相垂直证明它是菱形，可惜有一步错了.

（挑错改错）（1）小海的证明过程在第________步上开始出现了错误.

（2）请你根据小海的证题思路写出此题的正确解答过程，

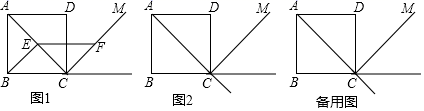
20．（8分）在正方形ABCD中，点E是射线AC上一点，点F是正方形ABCD外角平分线CM上一点，且CF=AE，连接BE，EF.

(1)如图1，当E是线段AC的中点时，直接写出BE与EF的数量关系；

(2)当点E不是线段AC的中点，其它条件不变时，请你在图2中补全图形，判断(1)中的结论是否成立，并证明你的结论；

(3)当点B，E，F在一条直线上时，求∠CBE的度数.(直接写出结果即可)

21．（10分）某同学上学期的数学历次测验成绩如下表所示：

（1）该同学上学期5次测验成绩的众数为      ，中位数为       ；

（2）该同学上学期数学平时成绩的平均数为         ；

（3）该同学上学期的总成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照2：3：5的比例计算所得，求该同学上学期数学学科的总评成绩（结果保留整数）。

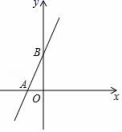
22．（10分）如图，点A的坐标为（﹣，0），点B的坐标为（0，3）．

（1）求过A，B两点直线的函数表达式；

（2）过B点作直线BP与x轴交于点P，且使OP=2OA，求△ABP的面积．

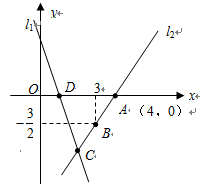
23．（12分）如图，直线的解析式为，且与轴交于点D，直线经过点、，直线、交于点C．

（1）求直线的解析表达式；

（2）求的面积；

（3）在直线上存在异于点C的另一点P，使得与的面积相等，请求出点P的坐标．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、D

2、A

3、D

4、B

5、B

6、D

7、A

8、D

9、D

10、C

11、D

12、A

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、

14、11-3k.

15、1

16、

17、1

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）①当x≤8000时，y=0；②当8000＜x≤30000时，y=0.5x﹣4000；③当30000＜x≤50000时，y=0.6x﹣7000；（2）1元．

19、（1）二; （2）见解析.

20、（1）EF=BE；（2）EF=BE，理由见解析；（3）当B，E，F在一条直线上时，∠CBE=22.5°

21、（1）106，106；（2）104 ；（3）107分.

22、（1）过A，B两点的直线解析式为y=2x+3；

（2）△ABP的面积为或．

23、（1）；（2）；（3）P（6，3）．