


2022-2023学年河北省霸州市部分学校数学七年级第二学期期末统考模拟试题含答案
展开
这是一份2022-2023学年河北省霸州市部分学校数学七年级第二学期期末统考模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,方程的解是,下列调查方法合适的是,若点P,下列调查中,不适宜用普查的是等内容,欢迎下载使用。
2022-2023学年河北省霸州市部分学校数学七年级第二学期期末统考模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.某社区超市以4元/瓶从厂家购进一批饮料,以6元/瓶销售.近期计划进行打折销售,若这批饮料的销售利润不低于20%则最多可以打( ) A.六折 B.七折 C.七五折 D.八折2.如图,直线
A.六折 B.七折 C.七五折 D.八折2.如图,直线![]() 的图象如图所示.下列结论中,正确的是( )
的图象如图所示.下列结论中,正确的是( ) A.
A.![]() B.方程
B.方程![]() 的解为
的解为![]() ;C.
;C.![]() D.若点A(1,m)、B(3,n)在该直线图象上,则
D.若点A(1,m)、B(3,n)在该直线图象上,则![]() .3.顺次连接对角线相等的四边形的各边中点,所形成的四边形是A.平行四边形 B.菱形 C.矩形 D.正方形4.方程
.3.顺次连接对角线相等的四边形的各边中点,所形成的四边形是A.平行四边形 B.菱形 C.矩形 D.正方形4.方程![]() 的解是A.
的解是A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]() 5.下列调查方法合适的是( )A.为了了解冰箱的使用寿命,采用普查的方式B.为了了解全国中学生的视力状况,采用普查的方式C.为了了解人们保护水资源的意识,采用抽样调查的方式D.对“神舟十一号载人飞船”零部件的检查,采用抽样调查的方式6.若点P(3,2m-1)在第四象限,则m的取值范围是( )A.
5.下列调查方法合适的是( )A.为了了解冰箱的使用寿命,采用普查的方式B.为了了解全国中学生的视力状况,采用普查的方式C.为了了解人们保护水资源的意识,采用抽样调查的方式D.对“神舟十一号载人飞船”零部件的检查,采用抽样调查的方式6.若点P(3,2m-1)在第四象限,则m的取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.如图,点
7.如图,点![]() 是矩形
是矩形![]() 两条对角线的交点,E是边
两条对角线的交点,E是边![]() 上的点,沿
上的点,沿![]() 折叠后,点
折叠后,点![]() 恰好与点
恰好与点![]() 重合.若
重合.若![]() ,则折痕
,则折痕![]() 的长为 ( )
的长为 ( )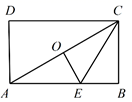 A.
A.![]() B.
B.![]() C.
C.![]() D.68.下列调查中,不适宜用普查的是()A.了解全班同学每周体育锻炼的时间; B.了解全市中小学生每天的零花钱;C.学校招聘教师,对应聘人员面试; D.旅客上飞机前的安检.9.某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示: 甲乙丙丁平均数/环
D.68.下列调查中,不适宜用普查的是()A.了解全班同学每周体育锻炼的时间; B.了解全市中小学生每天的零花钱;C.学校招聘教师,对应聘人员面试; D.旅客上飞机前的安检.9.某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示: 甲乙丙丁平均数/环![]()
![]()
![]()
![]() 方差/环
方差/环![]()
![]()
![]()
![]()
![]() 请你根据表中数据选一人参加比赛,最合适的人选是( )A.甲 B.乙 C.丙 D.丁10.如图所示的四边形,与选项中的四边形一定相似的是( )
请你根据表中数据选一人参加比赛,最合适的人选是( )A.甲 B.乙 C.丙 D.丁10.如图所示的四边形,与选项中的四边形一定相似的是( )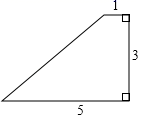 A.
A.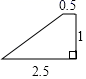 B.
B.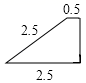 C.
C.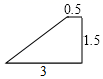 D.
D.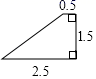 11.下列命题中,假命题是( )A.对角线互相平分的四边形是平行四边形B.对角线互相平分且相等的四边形是矩形C.对角线互相垂直平分的四边形是菱形D.对角线互相垂直且相等的四边形是正方形12.如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
11.下列命题中,假命题是( )A.对角线互相平分的四边形是平行四边形B.对角线互相平分且相等的四边形是矩形C.对角线互相垂直平分的四边形是菱形D.对角线互相垂直且相等的四边形是正方形12.如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )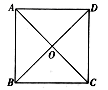 A.
A.![]() ,
,![]() B.
B.![]() C.
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.计算:
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.计算:![]() =__________.14.若
=__________.14.若![]() 是方程
是方程![]() 的两个实数根,则
的两个实数根,则![]() _______.15.如图,正方形
_______.15.如图,正方形![]() 的两边
的两边![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,点
轴上,点![]() 在边
在边![]() 上,以
上,以![]() 为中心,把
为中心,把![]() 旋转
旋转![]() ,则旋转后点
,则旋转后点![]() 的对应点
的对应点![]() 的坐标是________.
的坐标是________.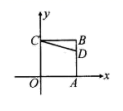 16.如图,平行四边形ABCD中,
16.如图,平行四边形ABCD中,![]() ,
,![]() ,
,![]() ,则平行四边形ABCD的面积为______.
,则平行四边形ABCD的面积为______.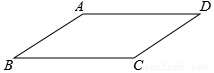 17.把直线y=﹣x﹣3向上平移m个单位,与直线y=2x+4的交点在第二象限,则m的取值范围是_____.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图矩形ABCD中,AB=12,BC=8,E、F分别为AB、CD的中点,点P、Q从A.C同时出发,在边AD、CB上以每秒1个单位向D、B运动,运动时间为t(0<t<8).
17.把直线y=﹣x﹣3向上平移m个单位,与直线y=2x+4的交点在第二象限,则m的取值范围是_____.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图矩形ABCD中,AB=12,BC=8,E、F分别为AB、CD的中点,点P、Q从A.C同时出发,在边AD、CB上以每秒1个单位向D、B运动,运动时间为t(0<t<8).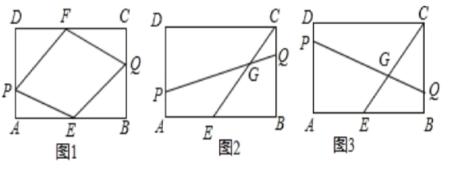 (1)如图1,连接PE、EQ、QF、PF,求证:无论t在0<t<8内取任何值,四边形PEQF总为平行四边形;(2)如图2,连接PQ交CE于G,若PG=4QG,求t的值;(3)在运动过程中,是否存在某时刻使得PQ⊥CE于G?若存在,请求出t的值:若不存在,请说明理由 19.(5分)某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的
(1)如图1,连接PE、EQ、QF、PF,求证:无论t在0<t<8内取任何值,四边形PEQF总为平行四边形;(2)如图2,连接PQ交CE于G,若PG=4QG,求t的值;(3)在运动过程中,是否存在某时刻使得PQ⊥CE于G?若存在,请求出t的值:若不存在,请说明理由 19.(5分)某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务,求原计划每小时抢修道路多少米? 20.(8分)如图,点C在线段AB上,过点C作CD⊥AB,点E,F分别是AD,CD的中点,连结EF并延长EF至点G,使得FG=CB,连结CE,GB,过点B作BH∥CE交线段EG于点H. (1)求证:四边形FCBG是矩形. (1)己知AB=10,
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务,求原计划每小时抢修道路多少米? 20.(8分)如图,点C在线段AB上,过点C作CD⊥AB,点E,F分别是AD,CD的中点,连结EF并延长EF至点G,使得FG=CB,连结CE,GB,过点B作BH∥CE交线段EG于点H. (1)求证:四边形FCBG是矩形. (1)己知AB=10,![]() . ①当四边形ECBH是菱形时,求EG的长.②连结CH,DH,记△DEH的面积为S1, △CBH的面积为S1.若EG=1FH,求S1+S1的值.
. ①当四边形ECBH是菱形时,求EG的长.②连结CH,DH,记△DEH的面积为S1, △CBH的面积为S1.若EG=1FH,求S1+S1的值.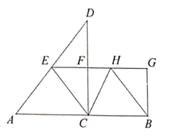 21.(10分)以四边形ABCD的边AB,AD为边分别向外侧作等边△ABF和等边△ADE,连接EB,FD,交点为G.(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由.
21.(10分)以四边形ABCD的边AB,AD为边分别向外侧作等边△ABF和等边△ADE,连接EB,FD,交点为G.(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由.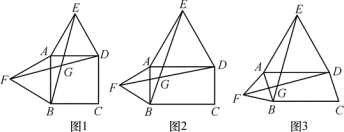 22.(10分)计算:(2
22.(10分)计算:(2![]() +3
+3![]() )2﹣2
)2﹣2![]() ×
×![]() ÷5
÷5![]() . 23.(12分)如图①,已知正方形ABCD的边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连接PQ、DQ、CQ、BQ,设AP=x.(1)BQ+DQ的最小值是_______,此时x的值是_______;(2)如图②,若PQ的延长线交CD边于点E,并且∠CQD=90°.①求证:点E是CD的中点; ②求x的值.(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x的值.
. 23.(12分)如图①,已知正方形ABCD的边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连接PQ、DQ、CQ、BQ,设AP=x.(1)BQ+DQ的最小值是_______,此时x的值是_______;(2)如图②,若PQ的延长线交CD边于点E,并且∠CQD=90°.①求证:点E是CD的中点; ②求x的值.(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x的值. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、D2、B3、B4、D5、C6、B7、A8、B9、A10、D11、D12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、114、1015、
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、D2、B3、B4、D5、C6、B7、A8、B9、A10、D11、D12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、114、1015、![]() 或
或![]() 16、1017、1<m<1. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)见解析;(2)
16、1017、1<m<1. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)见解析;(2)![]() ;(3)不存在,理由见解析.19、280米20、(1)证明见解析 (1)①
;(3)不存在,理由见解析.19、280米20、(1)证明见解析 (1)①![]() ②2或
②2或![]() 21、(1)EB=FD;(2)EB=FD,证明见解析;(3)∠EGD不发生变化.22、35+12
21、(1)EB=FD;(2)EB=FD,证明见解析;(3)∠EGD不发生变化.22、35+12![]() ﹣
﹣![]() .23、(1)
.23、(1)![]() ,
,![]() ;(3) ①理由详见解析;②
;(3) ①理由详见解析;②![]() ;(3) 3﹣
;(3) 3﹣![]() 或
或![]() 或3+
或3+![]() .
.
相关试卷
这是一份2023-2024学年河北省霸州市部分学校九年级数学第一学期期末经典试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
这是一份2023-2024学年河北省霸州市九上数学期末统考模拟试题含答案,共8页。
这是一份河北省霸州市部分学校2023-2024学年数学八上期末监测试题含答案,共8页。试卷主要包含了下列计算结果,正确的是,在,,,,中,分式的个数是等内容,欢迎下载使用。








