


北京十三中学分校2022-2023学年七年级数学第二学期期末调研模拟试题含答案
展开北京十三中学分校2022-2023学年七年级数学第二学期期末调研模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.如果把![]() 分式中的
分式中的![]() 、
、![]() 都扩大到10倍,那么分式的值( )
都扩大到10倍,那么分式的值( )
A.扩大10倍 B.不变 C.扩大20倍 D.是原来的![]()
2.星期天晚饭后,小丽的爸爸从家里出去散步,如图描述了她爸爸散步过程中离家的距离(km)与散步所用的时间(min)之间的函数关系,依据图象,下面描述符合小丽爸爸散步情景的是( )
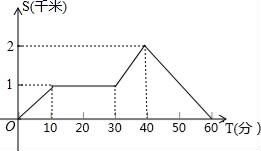
A.从家出发,休息一会,就回家
B.从家出发,一直散步(没有停留),然后回家
C.从家出发,休息一会,返回用时20分钟
D.从家出发,休息一会,继续行走一段,然后回家
3.下列曲线中,不能表示![]() 是
是![]() 的函数的是( )
的函数的是( )
A.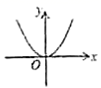 B.
B.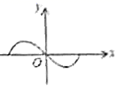 C.
C.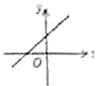 D.
D.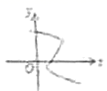
4.如图,在一个高为6米,长为10米的楼梯表面铺地毯,则地毯长度至少是( )
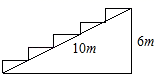
A.6米 B.10米 C.14米 D.16米
5.一次函数y=x+b的图像经过A(2,y1),B(4,y2),则y1和y2的大小关系为( )
A.y1>y2 B.y1≥y2 C.y1<y2 D.y1≤y2
6.若代数式![]() 有意义,则x的取值是( )
有意义,则x的取值是( )
A.x=2 B.x≠2 C.x=3 D.x≠﹣3
7.如图,已知平行四边形![]() 中,
中,![]() 则
则![]() ( )
( )
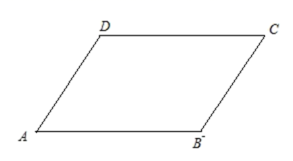
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(10,0),点B(0,6),点P为BC边上的动点,将△OBP沿OP折叠得到△OPD,连接CD、AD.则下列结论中:①当∠BOP=45°时,四边形OBPD为正方形;②当∠BOP=30°时,△OAD的面积为15;③当P在运动过程中,CD的最小值为1![]() ﹣6;④当OD⊥AD时,BP=1.其中结论正确的有( )
﹣6;④当OD⊥AD时,BP=1.其中结论正确的有( )
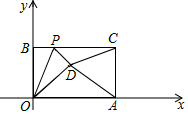
A.1个 B.1个 C.3个 D.4个
9.下列命题中,真命题是( )
A.两条对角线垂直的四边形是菱形
B.对角线垂直且相等的四边形是正方形
C.两条对角线相等的四边形是矩形
D.两条对角线相等的平行四边形是矩形
10.已知△ABC的三边分别是a,b,c,且满足|a-2![]() |+
|+![]() +(c-4)2=0,则以a,b,c为边可构成( )
+(c-4)2=0,则以a,b,c为边可构成( )
A.以c为斜边的直角三角形 B.以a为斜边的直角三角形
C.以b为斜边的直角三角形 D.有一个内角为![]() 的直角三角形
的直角三角形
二、填空题(本大题共有6小题,每小题3分,共18分)
11.若甲、乙、丙、丁四个同学一学期4次数学测试的平均成绩恰好都是85分,方差分别为s甲2=0.80,s乙2=1.31,s丙2=1.72,s丁2=0.42,则成绩最稳定的同学是______.
12.如图,边长为![]() 的菱形
的菱形![]() 中,
中,![]() ,连接对角线
,连接对角线![]() ,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…按此规律所作的第2019个菱形的边长为______.
,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…按此规律所作的第2019个菱形的边长为______.
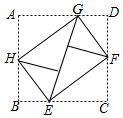
13.如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=6cm,GH=8cm,则边AB的长是__________
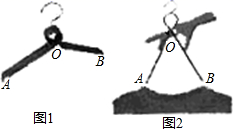
14.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图1,衣架杆OA=OB=18cm,若衣架收拢时,∠AOB=60°,如图2,则此时A,B两点之间的距离是____cm.
15.定义:等腰三角形的顶角与其一个底角的度数的比值![]() 称为这个等腰三角形的“特征值”.若等腰
称为这个等腰三角形的“特征值”.若等腰![]() 中,
中,![]() ,则它的特征值
,则它的特征值![]() __________.
__________.
16.已知一次函数![]() 经过
经过![]() ,且与y轴交点的纵坐标为4,则它的解析式为______.
,且与y轴交点的纵坐标为4,则它的解析式为______.
三、解下列各题(本大题共8小题,共72分)
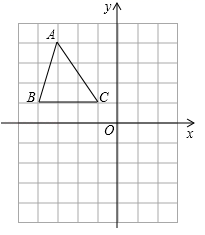
17.(8分)如图,在平面直角坐标系xOy中,A(-3,4),B(-4,1),C(-1,1).
(1)在图中作出△ABC关于x轴的轴对称图形△A′B′C′;
(2)直接写出A,B关于y轴的对称点A″,B″的坐标.
18.(8分)已知:如图,在四边形![]() 中
中![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,且
,且![]() .
.
求证:四边形![]() 是平行四边形.
是平行四边形.
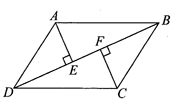
19.(8分)猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,试猜想DM与ME的数量关系,并证明你的结论.
拓展与延伸:
(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为__________________;
(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.[提示:直角三角形斜边上的中线等于斜边的一半]
 ①
① 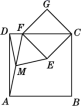 ②
②
20.(8分)垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
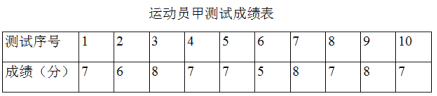
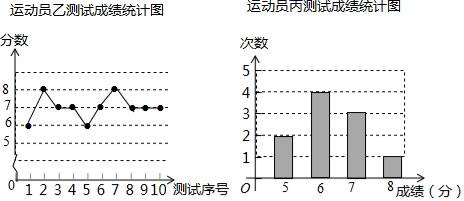
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)
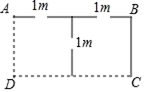
21.(8分)如图,利用两面靠墙(墙足够长),用总长度37米的篱笆(图中实线部分)围成一个矩形鸡舍ABCD,且中间共留三个1米的小门,设篱笆BC长为x米.
(1)AB=_____米.(用含x的代数式表示)
(2)若矩形鸡舍ABCD面积为150平方米,求篱笆BC的长.
(3)矩形鸡舍ABCD面积是否有可能达到210平方米?若有可能,求出相应x的值;若不可能,则说明理由.
22.(10分)如图,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.
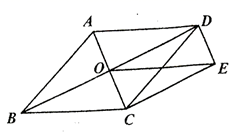
(1)求证:![]() ;
;
(2)探究:当![]() 等于多少度时,四边形
等于多少度时,四边形![]() 是正方形?并证明你的结论.
是正方形?并证明你的结论.
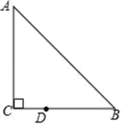
23.(10分)如图,在△ABC中,AC=BC,∠C=90°,D是BC上的一点,且BD=![]() CD.
CD.
(1)尺规作图:过点D作AB的垂线,交AB于点F;
(2)连接AD,求证:AD是△ABC的角平分线.
24.(12分)(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论;
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,猜测MN与BM的数量关系,无需证明.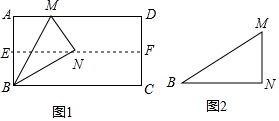
参考答案
一、选择题(每小题3分,共30分)
1、A
2、D
3、D
4、C
5、C
6、D
7、B
8、D
9、D
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、丁
12、![]()
13、![]() .
.
14、18
15、![]()
16、y=2x+1.
三、解下列各题(本大题共8小题,共72分)
17、 (1)见解析;(2)A″(3,4),B″(4,1).
18、证明见解析.
19、猜想与证明:猜想DM与ME的数量关系是:DM=ME,证明见解析;拓展与延伸:(1)DM=ME,DM⊥ME;(2)证明见解析
20、(1)众数是7,中位数是7;(2)乙,理由见解析
21、(1)40-2x(2)15米或5米(3)不可能
22、(1)见解析;(2)当![]() 时,四边形OCED为正方形,见解析.
时,四边形OCED为正方形,见解析.
23、 (1)见解析;(2)见解析.
24、(1)30º,见解析.(2)![]()
北京十三中学分校2023-2024学年数学九年级第一学期期末达标检测模拟试题含答案: 这是一份北京十三中学分校2023-2024学年数学九年级第一学期期末达标检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列图标中,是中心对称图形的是,如果,那么的值等于等内容,欢迎下载使用。
北京理工大附中分校2022-2023学年七年级数学第二学期期末经典模拟试题含答案: 这是一份北京理工大附中分校2022-2023学年七年级数学第二学期期末经典模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列说法正确的是,下列二次根式中能与2合并的是等内容,欢迎下载使用。
北京中学国人民大附属中学2022-2023学年七年级数学第二学期期末调研模拟试题含答案: 这是一份北京中学国人民大附属中学2022-2023学年七年级数学第二学期期末调研模拟试题含答案,共7页。试卷主要包含了要使分式有意义,的取值范围为,对点Q等内容,欢迎下载使用。












