北京理工大附中分校2022-2023学年七年级数学第二学期期末经典模拟试题含答案

北京理工大附中分校2022-2023学年七年级数学第二学期期末经典模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生请注意：

1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=5，则AE的长为(　　) 

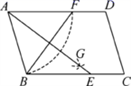
A．4 B．8 C．6 D．10

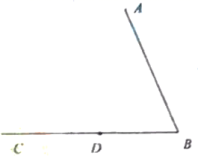
2．如图所示的3×3正方形网格中，∠1＋∠2＋∠3＋∠4＋∠5等于（     ）

A．135° B．180° C．225° D．270°

3．在四边形ABCD中，对角线AC、BD交于点O，下列条件中，不能判定四边形ABCD是平行四边形的是(　　  )

A．AB＝DC，AD＝BC B．AD∥BC，AD＝BC

C．AB∥DC，AD＝BC D．OA＝OC，OD＝OB

4．下列说法正确的是(　　)

A．一个游戏中奖的概率是,则做100次这样的游戏一定会中奖

B．为了了解全国中学生的心理健康状况,应采用普查的方式

C．一组数据0,1,2,1,1的众数和中位数都是1

D．若甲组数据的方差为,乙组数据的方差为,则乙组数据比甲组数据稳定

5．下列各组数据中，能作为直角三角形三边长的是（    ）

A．4，5，6 B．5，12，13 C．6，7，8 D．8，9，10

6．下列二次根式中能与2合并的是（　　）

A． B． C． D．

7．已知一次函数上有两点，，若，则、的关系是（   ）

A． B． C． D．无法判断

8．从﹣4，﹣3，﹣2，﹣1，0，1，3，4，5这九个数中，随机抽取一个数，记为a，则数a使关于x的不等式组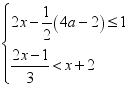至少有四个整数解，且关于x的分式方程＝1有非负整数解的概率是（　　）

A． B． C． D．

9．下表是小红填写的实践活动报告的部分内容:

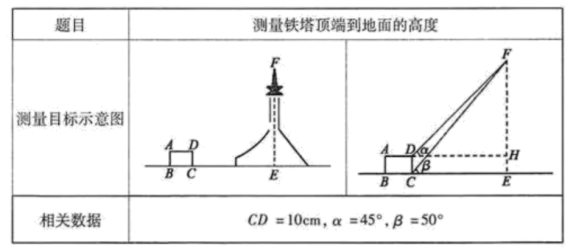
设铁塔顶端到地面的高度为，根据以上条件，可以列出的方程为（  ）

A． B．

C． D．

10．已知等腰△ABC的两边长分别为2和3，则等腰△ABC的周长为(　　)

A．7 B．8 C．6或8 D．7或8

二、填空题(本大题共有6小题，每小题3分，共18分)

11．若函数y=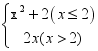，则当函数值y＝8时，自变量x的值等于_____．

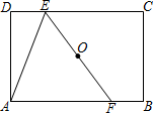
12．如图，在矩形ABCD中，AB=6，AD=4，过矩形ABCD的对角线交点O作直线分别交CD、AB于点E、F，连接AE，若△AEF是等腰三角形，则DE=______．

13．在一个不透明的布袋中，红色、黑色、白色的玻璃球共有60个，除颜色外，形状、大小、质地等完全相同．小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在15%和45%，则口袋中白色球的个数很可能是                 ．

14．计算的结果是______．

15．一个正多边形的每个内角度数均为135°，则它的边数为____．

16．把二次根式化成最简二次根式，则=____．

三、解下列各题(本大题共8小题，共72分)

17．（8分）用圆规和直尺作图，不写作法，保留作图痕迹.

已知及其边上一点.在内部求作点，使点到两边的距离相等，且到点，的距离相等.

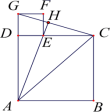
18．（8分）如图，已知四边形和四边形为正方形，点在线段上，点在同一直线上，连接，并延长交于点．

（1）求证：．

（2）若，，求线段的长．

（3）设，，当点H是线段GC的中点时，则与满足什么样的关系式.

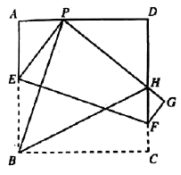
19．（8分）如图，现有一张边长为8的正方形纸片，点为边上的一点（不与点、点重合），将正方形纸片折叠，使点落在处，点落在处，交于，折痕为，连结、.

（1）求证：；

（2）求证：；

（3）当时，求的长.

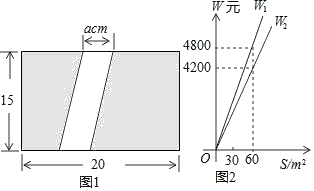
20．（8分）如图1，为美化校园环境，某校计划在一块长为20m，宽为15m的长方形空地上修建一条宽为a（m）的甬道，余下的部分铺设草坪建成绿地．

（1）甬道的面积为　   　m2，绿地的面积为　   　m2（用含a的代数式表示）；

（2）已知某公园公司修建甬道，绿地的造价W1（元），W2（元）与修建面积S之间的函数关系如图2所示．①园林公司修建一平方米的甬道，绿地的造价分别为　   　元，　   　元．②直接写出修建甬道的造价W1（元），修建绿地的造价W2（元）与a（m）的关系式；③如果学校决定由该公司承建此项目，并要求修建的甬道宽度不少于2m且不超过5m，那么甬道宽为多少时，修建的甬道和绿地的总造价最低，最低总造价为多少元？

21．（8分）在平面直角坐标系中，直线（且）与轴交于点，过点作直线轴，且与交于点.

（1）当，时，求的长；

（2）若，，且轴，判断四边形的形状，并说明理由.

22．（10分）解下列方程组和不等式组.（1）；（2）.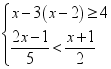

23．（10分）如图，直线与轴，轴分别交于点，点，与函数的图象交于点．

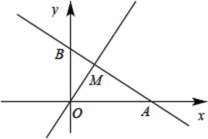
（1）直接写出k，b的值和不等式的解集；

（2）在轴上有一点，过点作轴的垂线，分别交函数和的图象于点，点．若，求点的坐标．

24．（12分）如图，已知二次函数的图象顶点在轴上，且，与一次函数的图象交于轴上一点和另一交点.

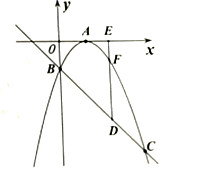
求抛物线的解析式；

点为线段上一点，过点作轴，垂足为，交抛物线于点，请求出线段的最大值.

参考答案

一、选择题(每小题3分,共30分)

1、B

2、C

3、C

4、C

5、B

6、B

7、A

8、C

9、A

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、或4

12、或1

13、24

14、1

15、8

16、 ．

三、解下列各题(本大题共8小题，共72分)

17、见解析.

18、（1）见解析；（2）；（3） （ ）.

19、（1）证明见解析；（2）证明见解析；（3）PH=．

20、（1）15a、（300﹣15a）；（2）①①80、70；；②W1＝80×15a＝1200a，W2＝70（300﹣15a）＝﹣1050a+21000；③甬道宽为2米时，修建的甬道和绿地的总造价最低，最低总造价为21300元；

21、（1）BC=1；（2）四边形OBDA是平行四边形，见解析．

22、（1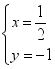）；（2）.

23、（1）不等式的解集为；（2）点的坐标为 ，或，．

24、 (1) ；（2）线段的最大值为.