

鲁科版(2019)高中物理 选择性必修第二册 第1章 章末综合提升学案
展开
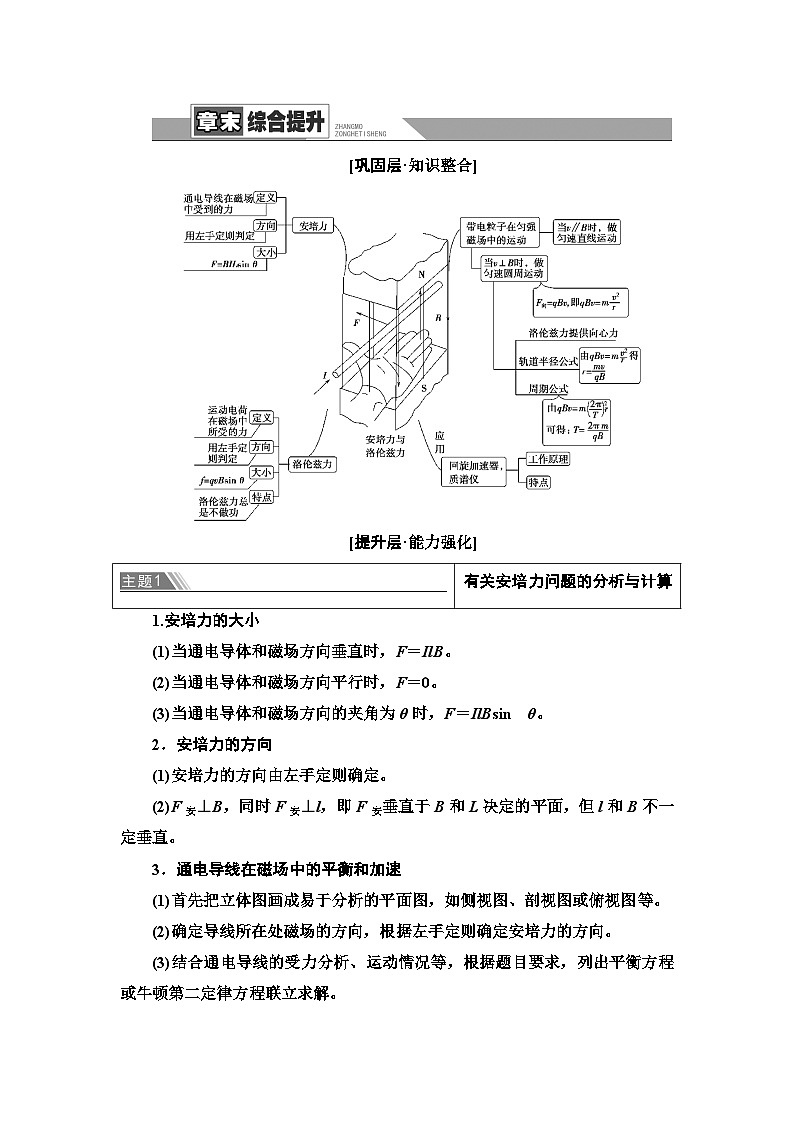
[巩固层·知识整合]
[提升层·能力强化]
| 有关安培力问题的分析与计算 |
1.安培力的大小
(1)当通电导体和磁场方向垂直时,F=IlB。
(2)当通电导体和磁场方向平行时,F=0。
(3)当通电导体和磁场方向的夹角为θ时,F=IlBsin θ。
2.安培力的方向
(1)安培力的方向由左手定则确定。
(2)F安⊥B,同时F安⊥l,即F安垂直于B和L决定的平面,但l和B不一定垂直。
3.通电导线在磁场中的平衡和加速
(1)首先把立体图画成易于分析的平面图,如侧视图、剖视图或俯视图等。
(2)确定导线所在处磁场的方向,根据左手定则确定安培力的方向。
(3)结合通电导线的受力分析、运动情况等,根据题目要求,列出平衡方程或牛顿第二定律方程联立求解。
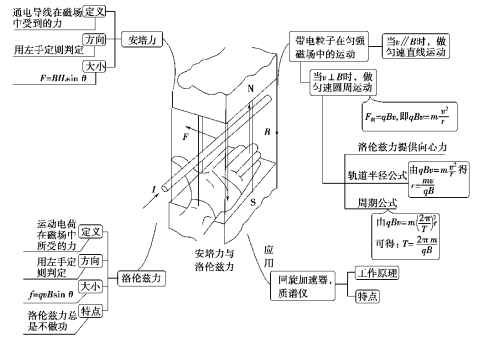
【例1】 如图所示,在倾角θ=30°的斜面上固定一平行金属导轨,导轨间距离l=0.25 m,两导轨间接有滑动变阻器R和电动势E=12 V、内阻不计的电池。垂直导轨放有一根质量m=0.2 kg的金属棒ab,它与导轨间的动摩擦因数μ=。整个装置放在垂直斜面向上的匀强磁场中,磁感应强度B=0.8 T。当调节滑动变阻器R的阻值在什么范围内时,可使金属棒静止在导轨上(导轨与金属棒的电阻不计,g取10 m/s2)。
思路点拨:金属棒受到四个力的作用:重力mg、垂直斜面向上的支持力N、沿斜面向上的安培力F和沿斜面方向的摩擦力f。金属棒静止在导轨上时,摩擦力f的方向可能沿斜面向上,也可能沿斜面向下,需分两种情况考虑。
[解析] 当滑动变阻器R接入电路的阻值较大时,I较小,安培力F较小,金属棒在重力沿斜面的分力mgsin θ作用下有沿斜面下滑的趋势,导轨对金属棒的摩擦力沿斜面向上(如图甲所示)。
金属棒刚好不下滑时有Bl+μmgcos θ-mgsin θ=0
解得R==4.8 Ω

当滑动变阻器R接入电路的阻值较小时,I较大,安培力F较大,会使金属棒产生沿斜面上滑的趋势,此时导轨对金属棒的摩擦力沿斜面向下(如图乙所示)。金属棒刚好不上滑时有
Bl-μmgcos θ-mgsin θ=0
解得R==1.6 Ω
所以,滑动变阻器R接入电路的阻值范围应为1.6 Ω≤R≤4.8 Ω。
[答案] 1.6 Ω≤R≤4.8 Ω
[一语通关]
1.在安培力作用下的物体的平衡问题的解决步骤和前面学习的共点力平衡相似,一般也是先进行受力分析,再根据共点力平衡的条件列出平衡方程,注意在受力分析过程中不要漏掉安培力。对物体进行受力分析时,注意安培力大小和方向的确定。
2.为方便对问题分析和便于列方程,在受力分析时应将立体图画成平面图,即画成俯视图、剖面图或侧视图等。将抽象的空间受力分析转移到纸面上进行,最后结合正交分解或平行四边形定则进行分析。
| 带电粒子在洛伦兹力作用下的多解问题 |
1.带电粒子的电性不确定形成多解
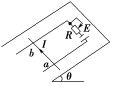
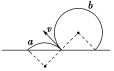
受洛伦兹力作用的带电粒子,可能带正电,也可能带负电,当粒子具有相同速度时,正负粒子在磁场中运动轨迹不同,导致多解。如图所示,带电粒子以速率v垂直进入匀强磁场,若带正电,其轨迹为a;若带负电,其轨迹为b。
2.磁场方向的不确定形成多解
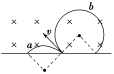
磁感应强度是矢量,如果题述条件只给出磁感应强度的大小,而未说明磁感应强度的方向,则应考虑因磁场方向不确定而导致的多解。如图所示,带正电的粒子以速率v垂直进入匀强磁场,若B垂直纸面向里,其轨迹为a,若B垂直纸面向外,其轨迹为B。
3.临界状态不唯一形成多解
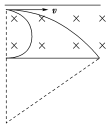
带电粒子在洛伦兹力作用下飞越有界磁场时,由于粒子运动轨迹是圆弧状,因此,它可能穿过去了,也可能转过180°从入射面边界反向飞出,如图所示,于是形成了多解。
4.运动的往复性形成多解
带电粒子在部分是电场、部分是磁场的空间运动时,运动往往具有往复性,从而形成多解,如图所示。
【例2】 如图所示,abcd是一个边长为L的正方形,它是磁感应强度为B的匀强磁场横截面的边界线。一带电粒子从ad边的中点O与ad边成θ=30°角且垂直于磁场方向射入。若该带电粒子所带电荷量为q、质量为m(重力不计),则该带电粒子在磁场中飞行时间最长是多少?若要带电粒子飞行时间最长,带电粒子的速度必须符合什么条件?
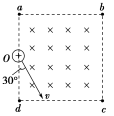
[解析] 从题设的条件中,可知带电粒子在磁场中只受洛伦兹力作用,做匀速圆周运动,粒子带正电,由左手定则可知它将向ab方向偏转,带电粒子可能的轨迹如图所示(磁场方向没有画出),由图可以发现带电粒子从入射边进入,又从入射边飞出时,其轨迹所对的圆心角最大,那么,带电粒子从ad边飞出的轨迹中,与ab相切的轨迹半径也就是它所有可能轨迹半径中的临界半径r0:r>r0,在磁场中运动时间是变化的,r≤r0,在磁场中运动的时间是相同的,也是在磁场中运动时间最长的。由图可知,∠OO2E=。
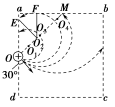
轨迹所对的圆心角为α=2π-=
运动的时间t=T=
由图还可以得到
r0+=,r0=≥
得v≤
故带电粒子在磁场中飞行时间最长是;带电粒子的速度必须符合条件v≤。
[答案] v≤
[一语通关]
求解带电粒子在磁场中运动多解问题的技巧
(1)分析题目特点,确定题目多解性形成原因。
(2)作出粒子运动轨迹示意图(全面考虑多种可能性)。
(3)若为周期性重复的多解问题,寻找通项式,若是出现几种解的可能性,注意每种解出现的条件。
| 带电粒子在复合场中的运动 |
1.复合场
复合场是指重力场、磁场、电场三者或任意两者的组合或叠加。
2.受力分析
带电粒子在重力场、电场、磁场中运动时,其运动状态的改变由粒子受到的合力决定,因此,对带电粒子进行受力分析时必须注意是否考虑重力,具体情况如下。
(1)对于微观粒子,如电子、质子、离子等,若无特殊说明,一般不考虑重力;对于宏观带电物体,如带电小球、尘埃、油滴、液滴等,若无特殊说明,一般需要考虑重力。
(2)对于题目中明确说明需要考虑重力的,这种情况较简单。
(3)不能直接判断是否需要考虑重力的,在进行受力分析和运动分析时,由分析结果确定是否考虑重力。
3.带电粒子在复合场中运动的几种情况及解决方法
(1)当带电粒子所受合力为零时,将处于静止或匀速直线运动状态。应利用平衡条件列方程求解。
(2)当带电粒子做匀速圆周运动时,洛伦兹力提供向心力,其余各力的合力必为零。一般情况下是重力和电场力平衡,应利用平衡方程和向心力公式求解。
(3)当带电粒子所受合力大小与方向均变化时,粒子将做非匀速曲线运动,带电粒子所受洛伦兹力必不为零,且其大小和方向不断变化,但洛伦兹力不做功,这类问题一般应用动能定理求解。
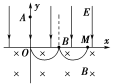
【例3】 在平面直角坐标系xOy中,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限存在垂直于坐标平面向外的匀强磁场,磁感应强度为B。一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示。不计粒子重力,求:
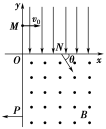
(1)M、N两点间的电势差UMN;
(2)粒子在磁场中运动的轨道半径r;
(3)粒子从M点运动到P点的总时间t。
[解析] (1)设粒子过N点时的速度为v,有
=cos θ,得v=2v0
粒子从M点运动到N点的过程中有
qUMN=mv2-mv
解得UMN=。
(2)如图所示,粒子在磁场中以O′为圆心做匀速圆周运动,半径为O′N,有
qvB=,解得r=。
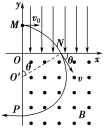
(3)由几何关系得ON=rsin θ
设粒子在电场中运动的时间为t1,有ON=v0t1,解得t1=
粒子在磁场中做匀速圆周运动的周期T=
设粒子在磁场中运动的时间为t2,有
t2=T,解得t2=
则粒子从M点运动到P点的总时间
t=t1+t2=。
[答案] (1) (2) (3)
[一语通关]
带电粒子在复合场中运动问题的处理方法
(1)首先要弄清复合场的组成。其次,要正确地对带电粒子进行受力分析和运动过程分析。在进行受力分析时要注意洛伦兹力方向的判定方法——左手定则。在分析运动过程时,要特别注意洛伦兹力的特点——始终和运动方向垂直,不做功。最后,选择合适的动力学方程进行求解。
(2)带电粒子在复合场中的运动问题是电磁学知识和力学知识的结合,分析方法和力学问题的分析方法基本相同,不同之处是多了静电力和洛伦兹力。因此,带电粒子在复合场中的运动问题要注意电场和磁场对带电粒子的作用特点,如静电力做功与路径无关,洛伦兹力方向始终和速度方向垂直且永不做功等。
[培养层·素养升华]
正负电子对撞机——揭示微观世界的奥秘
正负电子对撞机是一个使正负电子产生对撞的设备,它将各种粒子(如质子、电子等)加速到极高的能量,然后使粒子轰击一固定靶。通过研究高能粒子与靶中粒子碰撞时产生的各种反应研究其反应的性质,发现新粒子、新现象。正负电子对撞是一种正负粒子碰撞的机制,正电子与负电子在自然界已有产出,人们研究微电子粒子的结构特性,是当今高能粒子物理与量子力学的最前沿的科学。
北京正负电子对撞机(BEPC)是世界八大高能加速器之一, 是我国第一台高能加速器,也是高能物理研究的重大科技基础设施。由电子枪产生的电子,和电子打靶产生的正电子,在加速器里加速到15亿电子伏特,输入到储存环。正负电子在储存环里,可以22亿电子伏即接近光的速度相向运动、回旋、加速,并以每秒125万次不间断地进行对撞。而每秒有价值的对撞只有几次。有着数万个数据通道的北京谱仪,犹如几万只眼睛,实时观测对撞产生的次级粒子,所有数据自行传输到计算机中。科学家通过对这些数据的处理和分析,进一步认识粒子的性质,从而揭示微观世界的奥秘。

[设问探究]
1.北京正负电子对撞机(BEPC)是世界八大高能加速器中心之一, 是我国第一台高能加速器。其加速的原理是什么?如何计算电子的速度?
2.正负电子在储存环里,可以22亿电子伏即接近光的速度相向运动、回旋、加速,并以每秒125万次不间断地进行对撞。其回旋的原理是什么?其回旋的周期如何计算?
提示:
1.利用电场加速,可根据加速电压应用动能定理计算其速度,即有eU=mv2,故v=。
2.电子回旋运动的原理是在磁场中做圆周运动,可根据洛伦兹力充当向心力计算其周期,即有T=。
[深度思考]
(多选)环形对撞机是研究高能离子的重要装置,如图所示正、负离子由静止经过电压为U的直线加速器加速后,沿圆环切线方向注入对撞机的真空环状空腔内,空腔内存在着与圆环平面垂直的匀强磁场,磁感应强度大小为B。(两种带电粒子将被局限在环状空腔内,沿相反方向做半径相等的匀速圆周运动,从而在碰撞区迎面相撞)为维持带电粒子在环状空腔中的匀速圆周运动,下列说法正确的是( )
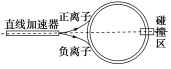
A.对于给定的加速电压,带电粒子的比荷越大,磁感应强度B越大
B.对于给定的加速电压,带电粒子的比荷越大,磁感应强度B越小
C.对于给定的带电粒子,加速电压U越大,粒子运动的周期越小
D.对于给定的带电粒子,不管加速电压U多大,粒子运动的周期都不变
思路分析:解此题的关键是掌握正负离子运动的原理,即电场中的加速和磁场中的圆周运动。
BC [在加速器中有qU=mv2,在环状空腔内做匀速圆周运动的半径r=,即r= ,所以在半径不变的条件下,越大,B越小,选项B正确;粒子在空腔内的周期T=,故加速电压越大,粒子的速率v越大,其周期越小,选项C正确。]
[素养点评] 本题是联系现代科技的考题,将复杂的正负离子的对撞抽象为简单的物理模型,考查学生对带电粒子在电磁场中运动规律的处理能力,学生只有掌握带电粒子在电场中加速和在磁场中圆周运动的处理方法,才能顺利解决此类问题,体现科学思维与科学态度与责任在物理教学中的重要意义。










