初中浙教版2.6 有理数的混合运算精练

2.6有理数的混合运算培优

一、单选题

1．根据如图所示的程序计算，若输入x的值为1，则输出y的值为（　　）

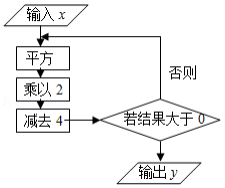
A．4 B．﹣2 C．8 D．3

2．定义一种对正整数n的“F”运算：①当n为奇数时=3n+1；②当n为偶数时,=（其中k是使为奇数的正整数）……，两种运算交替重复进行，例如，取n=24则：

若n=13，则第2019次“F”运算的结果是（    ）

A．1 B．4 C．2019 D．42019

3．如图所示是一个运算程序的示意图，若开始输入的x值为27，则第5次输出的结果为  

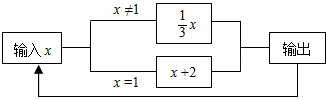
A．3 B．27 C．9 D．1

4．现定义运算“*”，对于任意有理数a，b满足a*b＝．如5*3＝2×5﹣3＝7，*1＝﹣2×1＝﹣，若x*3＝5，则有理数x的值为（　　）

A．4 B．11 C．4或11 D．1或11

5．（-2）2004+3×（-2）2003的值为 （ ）

A．-22003 B．22003 C．-22004 D．22004

6．已知，则式子：（   ）

A．3 B．或1 C．或3 D．1

7．为了求1＋2＋22＋23＋…＋22019的值，可令S＝1＋2＋22＋23＋…＋22019，则2S＝2＋22＋23＋…＋22019＋22020，因此2S－S＝22020－1，所以1＋2＋22＋23＋…＋22019＝22020－1.请仿照以上推理计算：1＋4＋42＋43＋…＋42019的值是(     ）

A．42100－1 B．42020－1 C． D．

8．已知和是一对互为相反数，的值是（   ）

A． B． C． D．

二、填空题

9．计算：_________．

10．定义一种新运算：新定义运算，则的结果是______．11．已知有理数a，b满足ab＜0，a+b＞0，7a+2b+1=﹣|b﹣a|，则 的值为_____．

12．对于正数x规定，例如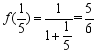：，，，则f (2019)＋f (2018)＋……＋f (2)＋f (1)＋＝___________．

13．对于正数x，规定f（x）=，例如f（2）=，f()=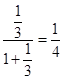，根据规定，计算f（1）+f（2）+f（3）+…+f（2015）+f()+f()+f()+…+f()=________．

14．设一种运算程序是xy=a（a为常数），如果(x+1) y=a+1，x (y+1)=a-2，已知11=2，那么20102010=_____________．

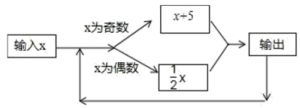
15．如图所示的运算程序中，若开始输入的x值为48，我们发现第1次输出的结果为24，第2次输出的结果为12，…第207次输出的结果为________．

16．计算＝_______．

三、解答题

17．计算：

（1）5﹣4×（﹣）﹣|﹣3|

（2）﹣12018+0.5÷（﹣）3×[3﹣（﹣2）]

18．已知数轴上两点A、B所表示的数分别为a和b，且满足|a＋3|＋(b－9)2018＝0，O为原点

(1) 试求a和b的值

(2) 点C从O点出发向右运动，经过3秒后点C到A点的距离是点C到B点距离的3倍，求点C的运动速度？

(3) 点D以1个单位每秒的速度从点O向右运动，同时点P从点A出发以5个单位每秒的速度向左运动，点Q从点B出发，以20个单位每秒的速度向右运动．在运动过程中，M、N分别为PD、OQ的中点，问的值是否发生变化，请说明理由.

19．计算：

(1)；

(2)[(－3)3－(－5)3]÷[(－3)－(－5)]；

(3)；

(4)．

20．计算：

（1）

（2）

21．已知：在一条东西向的双轨铁路上迎面驶来一快一慢两列火车，快车长(单位长度)，慢车长(单位长度)，设正在行驶途中的某一时刻，如图，以两车之间的某点为原点，取向右方向为正方向画数轴，此时快车头在数轴上表示的数是，慢车头在数轴上表示的数是.若快车以6个单位长度/秒的速度向右匀速继续行驶，同时慢车以2个单位长度/秒的速度向左匀速继续行驶，且与互为相反数．

（1）求此时多快车头与慢车头之间相距多少单位长度？

（2）从此时刻开始算起，问再行驶多少秒钟两列火车行驶到车头相距8个单位长度？

（3）此时在快车上有一位爱动脑筋的七年级学生乘客，他发现行驶中有一段时间，他的位置到两列火车头、的距离和加上到两列火车尾、的距离和是一个不变的值(即为定值)．你认为学生发现的这一结论是否正确？若正确，请直接写出这个定值：若不正确，请说明理由．

22．某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实

际每天生产量与计划量相比有出入，下表是某周的生产情况（超产记为正、减产记为负）：

（1）根据记录的数据可知该厂星期四生产自行车         辆：

（2）产量最多的一天比产量最少的一天多生产自行车        辆：

（3）根据记录的数据可知该厂本周实际生产自行车        辆；

（4）该厂实行每周计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖20元；少生产一辆扣25元，那么该厂工人这一周的工资总额是多少元？

23．海峰上星期六（周日股市不交易）买进某公司股票1000股，每股30元，下表为本周内每日股票的涨跌情况：

（1）星期三收盘时，每股是多少元？

（2）本周内最高价是每股多少元？最低价是多少元？

（3）已知海峰买进股标时付了的手续费，卖出时需付成交额的0.15%的手续费和0.1%的交易税，如果海峰在星期六收盘前将全部股票卖出，他的收益为多少元？

24．（概念学习）规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等．类比有理数的乘方，我们把2÷2÷2记作2③，读作“2的圈3次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）记作（﹣3）④，读作“﹣3的圈4次方”，一般地，把 （a≠0）记作aⓝ，读作“a的圈n次方”．

（1）（初步探究）

直接写出计算结果：2③=_______，（-）⑤=_______；

（2）（深入思考）

我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？

Ⅰ.试一试：仿照上面的算式，将下列运算结果直接写成幂的形式．

（﹣3）④=_______；5⑥=_______； (-) ⑩=_______．

Ⅱ. 想一想：将一个非零有理数a的圈n次方写成幂的形式等于_______；

Ⅲ.  算一算：

12²÷(-)④×(-2)⑤－(-)⑥÷3³.

25．（概念学习）规定：求若干个相同的有理数（均不等0）的除法运算叫做除方，如，等．类比有理数的乘方，我们把记作，读作“2的圈3次方”记作，读作“的圈4次方”．一般地，把记作读作“a的圈n次方”

（初步探究）

（1）直接写出计算结果：________，________．

（2）关于除方，下列说法错误的是________

A．任何非零数的圈3次方都等于它的倒数

B．对于任何正整数n，1=1

C．

D．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数

（深入思考）

我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘法运算呢？

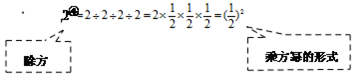
（3）试一试：仿照上面的算式，将下列运算结果直接写成幂的形式

________；_________；_______

（4）想一想：将一个非零有理数a的圈n次方写成幂的形式是________

（5）算一算：．

26．某天上午，一出租车司机始终在一条南北走向的笔直马路上营运，(出发点记作为点O，约定向南为正，向北为负)，期间一共运载6名乘客，行车里程(单位：千米)依先后次序记录如下：﹢7，﹣3，﹢6，﹣1，﹢2，﹣4.

(1)出租车在行驶过程中，离出发点O最远的距离是______千米；

(2)将最后一名乘客送到目的地，出租车离出发点O多远？在O点的什么方向？

(3)出租车收费标准为：起步价(不超过3千米)为8元，超过3千米的部分每千米的价格为1.5元，求司机这天上午的营业额.