


湘教版八年级上册5.1 二次根式优秀课后作业题
展开第5章 二次根式
5.1 二次根式
基础过关全练
知识点1 二次根式的定义
1.(2022广西柳州柳南期末)下列各式中,一定是二次根式的是( )
A.![]()
知识点2 二次根式有意义的条件
2.(2021湖南永州中考)已知二次根式![]() 有意义,则x的取值范围是 .
有意义,则x的取值范围是 .
3.当x是何实数时,下列二次根式有意义?
(1)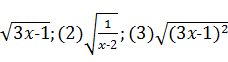 .
.
知识点3 二次根式的性质
4.(2022湖南长沙期末)在实数范围内要使![]() =a-2成立,则a的取值范围是( )
=a-2成立,则a的取值范围是( )
A.a=2 B.a>2 C.a≥2 D.a≤2
5.计算:
(1)(![]() )2= ;
)2= ;
(2)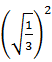 = ;
= ;
(3)(2![]() )2= ;
)2= ;
(4)(-3![]() )2= .
)2= .
6.计算:
(1)![]() = ;
= ;
(2)![]() = ;
= ;
(3)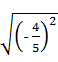 = ;
= ;
(4)![]() = .
= .
7.(2022独家原创)已知实数a,b在数轴上对应点的位置如图所示,化简![]() 的结果为 .
的结果为 .
![]()
8.设a,b,c为△ABC的三边的长,化简:
![]() .
.
9.当x的取值范围是不等式组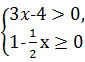 的解集时,试化简:
的解集时,试化简:
![]() -x.
-x.
知识点4 积的算术平方根
10.化简![]() 的结果是( )
的结果是( )
A.-3![]() C.6 D.18
C.6 D.18
11.当a<2时,化简![]() 的结果是( )
的结果是( )
A.a![]()
C.a![]()
12.计算:
(1)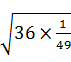 = ;
= ;
(2)![]() = ;
= ;
(3)![]() = .
= .
知识点5 最简二次根式
13.(2022湖南岳阳临湘期末)下列为最简二次根式的是( )
A.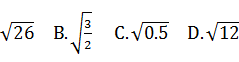
14.下列各式中,哪些是最简二次根式?哪些不是?对不是最简二次根式的进行化简.
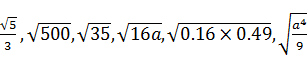 .
.
能力提升全练
15.(2021黑龙江绥化中考,4,![]() )若式子
)若式子![]() 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
A.x>-1 B.x≥-1且x≠0
C.x>-1且x≠0 D.x≠0
16.(2022湖南娄底娄星期末,7,![]() )下列根式不是最简二次根式的是( )
)下列根式不是最简二次根式的是( )
A.![]()
C.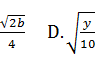
17.(2021辽宁大连中考,7,![]() )下列计算正确的是( )
)下列计算正确的是( )
A.(-![]() )2=-3
)2=-3
B.![]()
C.![]() =1
=1
D.(![]() -1)=3
-1)=3
18.(2021湖南娄底中考,8,![]() )2、5、m是某三角形三边的长,则
)2、5、m是某三角形三边的长,则![]() 等于( )
等于( )
A.2m-10 B.10-2m
C.10 D.4
19.(2021湖北武汉中考,11,![]() )计算
)计算![]() 的结果是 .
的结果是 .
20.(2021湖南岳阳华容期末,13,![]() )若|a+1|+
)若|a+1|+![]() +(c-3)2=0,则a-b+c= .
+(c-3)2=0,则a-b+c= .
21.(2022湖南永州期末,16,![]() )定义一种新的运算“@”,“@”的运算法则为a@b=
)定义一种新的运算“@”,“@”的运算法则为a@b=![]() ,则(2@3)@5= .
,则(2@3)@5= .
22.(2020甘肃陇南中考,18,![]() )已知y=
)已知y=![]() -x+5,当x分别取1,2,3,…,2 020时,所对应y值的总和是 .
-x+5,当x分别取1,2,3,…,2 020时,所对应y值的总和是 .
素养探究全练
23.[数学运算](2022吉林长春期末)【阅读材料】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() )2.善于思考的小明进行了以下探索:若设a+b
)2.善于思考的小明进行了以下探索:若设a+b![]() (其中a、b、m、n均为整数),则有a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b
(其中a、b、m、n均为整数),则有a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
【问题解决】
(1)若a+b![]() )2,当a、b、m、n均为整数时,
)2,当a、b、m、n均为整数时,
a= ,b= ;(均用含m、n的式子表示)
(2)若x+4![]() )2,且x、m、n均为正整数,分别求出x、m、n的值;
)2,且x、m、n均为正整数,分别求出x、m、n的值;
【拓展延伸】
(3)化简:![]() = .
= .
24.[数学运算](2022湖南长沙雨花期末)先观察下列等式,再回答问题.
①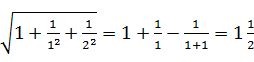 ;
;
②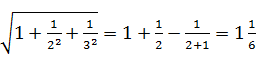 ;
;
③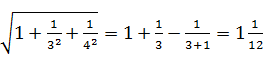 .
.
(1)根据上面三个等式提供的信息,请你猜想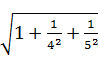 的结果;
的结果;
(2)请用含n的式子表示上面各等式反映的规律;
(3)利用上面的规律计算:
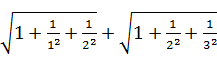 +…+
+…+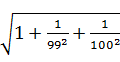 .
.
答案全解全析
基础过关全练
1.D ∵a2+1>0,∴![]() 一定是二次根式.
一定是二次根式.
2.x≥-3
解析 ∵二次根式![]() 有意义,
有意义,
∴x+3≥0,解得x≥-3.
3.解析 (1)要使![]() 在实数范围内有意义,则3x-1≥0,解得x≥
在实数范围内有意义,则3x-1≥0,解得x≥![]() .
.
(2)要使![]() 在实数范围内有意义,则x-2>0,解得x>2.
在实数范围内有意义,则x-2>0,解得x>2.
(3)∵(3x-1)2≥0,
∴当x取任何实数时,![]() 在实数范围内都有意义.
在实数范围内都有意义.
4.C ∵![]() =|a-2|=a-2,
=|a-2|=a-2,
∴a-2≥0,解得a≥2.
5.(1)3 (2)![]() (3)20 (4)54
(3)20 (4)54
解析 (1)(![]() )2=3.
)2=3.
(2)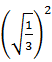 =
=![]() .
.
(3)(2![]() )2=4×5=20.
)2=4×5=20.
(4)(-3![]() )2=9×6=54.
)2=9×6=54.
6.(1)8 (2)![]() (3)
(3)![]() (4)π-3.14
(4)π-3.14
解析 根据![]() =|a|=
=|a|=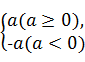 进行计算.
进行计算.
7.a
解析 由题中数轴知b<a<0,
∴a-b>0,
∴![]() -
-![]() =a-b-(-b)=a-b+b=a.
=a-b-(-b)=a-b+b=a.
8.解析 根据a,b,c为△ABC的三边的长,得到a+b+c>0,a-b-c<0,
b-a-c<0,c-b-a<0,
则原式=|a+b+c|+|a-b-c|+|b-a-c|-|c-b-a|
=a+b+c+b+c-a+a+c-b+c-b-a=4c.
9.解析 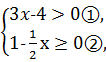
解不等式①,得x>![]() ,
,
解不等式②,得x≤2,
∴x的取值范围是![]() <x≤2,
<x≤2,
∴1-2x<0,x-3<0,
∴(![]() )2+
)2+![]() -x
-x
=|1-2x|+|x-3|-x=2x-1-x+3-x=2.
10.B 原式=![]() ×
×![]() =3
=3![]() .
.
11.B ∵a<2,∴a-2<0,
∵a3(a-2)≥0,
∴a≤0,
∴![]() =-a
=-a![]() .
.
12.(1)![]() (2)36 (3)4
(2)36 (3)4![]()
解析 (1)原式=![]() ×
×![]() =6×
=6×![]() =
=![]() .
.
(2)原式=![]() =
=![]() =
=![]() =36.
=36.
(3)原式=![]() =
=![]() =4
=4![]() .
.
13.A ![]() 是最简二次根式.故选A.
是最简二次根式.故选A.
14.解析 最简二次根式有![]() ,
,![]() ,其余的都不是最简二次根式.化简如下:
,其余的都不是最简二次根式.化简如下:![]() =10
=10![]() ,
,![]() =4
=4![]() ,
,![]() =0.28,
=0.28,![]() =
=![]() .
.
能力提升全练
15.C ∵式子![]() 在实数范围内有意义,
在实数范围内有意义,
∴x+1>0且x≠0,解得x>-1且x≠0.
16.D ![]() 不是最简二次根式,故选D.
不是最简二次根式,故选D.
17.B (-![]() )2=3,
)2=3,![]() =2
=2![]() ,
,![]() =-1,(
=-1,(![]() +1)×(
+1)×(![]() -1)=2-1=1,故选B.
-1)=2-1=1,故选B.
18.D ∵2、5、m是某三角形三边的长,
∴5-2<m<5+2,即3<m<7,
∴![]() +
+![]() =m-3+7-m=4.
=m-3+7-m=4.
19.5
解析 ![]() =|-5|=5.
=|-5|=5.
20.4
解析 ∵|a+1|≥0,![]() ≥0,(c-3)2≥0,且|a+1|+
≥0,(c-3)2≥0,且|a+1|+![]() +(c-3)2=0,
+(c-3)2=0,
∴a+1=0,b+2=0,c-3=0,解得a=-1,b=-2,c=3,∴a-b+c=-1-(-2)+3=4.
21.3![]()
解析 根据题意得(2@3)@5=![]() @5=
@5=![]() @5=3@5
@5=3@5
=![]() =
=![]() =3
=3![]() .
.
22.2 032
解析 当x<4时,y=4-x-x+5=-2x+9,当x=1时,y=7;当x=2时,y=5;当x=3时,y=3,当x≥4时,y=x-4-x+5=1,∴当x分别取1,2,3,…,2 020时,所对应y值的总和是7+5+3+1+1+…+1=15+1×2 017=2 032.
素养探究全练
23.解析 (1)m2+5n2;2mn.
(2)(m+n![]() )2=m2+2mn
)2=m2+2mn![]() +3n2,
+3n2,
∵x+4![]() =(m+n
=(m+n![]() )2,
)2,
∴![]()
又∵x、m、n均为正整数,
∴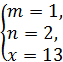 或
或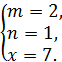
(3)原式=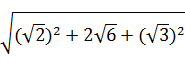
=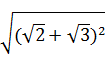
=![]() +
+![]() ,
,
故答案为![]() +
+![]() .
.
24.解析 (1)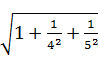 =1+
=1+![]() -
-![]() =1
=1![]() .
.
(2)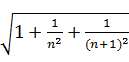 =1+
=1+![]() -
-![]() =1+
=1+![]() .
.
(3)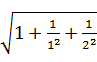 +
+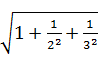 +…+
+…+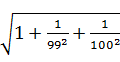
=1+![]() -
-![]() +1+
+1+![]() -
-![]() +…+1+
+…+1+![]() -
-![]()
=1×99+1-![]() =99
=99![]() .
.
湘教版八年级上册5.1 二次根式优秀精练: 这是一份湘教版八年级上册5.1 二次根式优秀精练,共6页。试卷主要包含了1 二次根式》同步练习,下列各式一定是二次根式的是,下列式子等内容,欢迎下载使用。
初中数学湘教版八年级上册5.1 二次根式优秀课后作业题: 这是一份初中数学湘教版八年级上册5.1 二次根式优秀课后作业题,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
湘教版第5章 二次根式5.1 二次根式优秀当堂检测题: 这是一份湘教版第5章 二次根式5.1 二次根式优秀当堂检测题,共10页。试卷主要包含了下列计算正确的是,下列各式中,计算结果为的是,计算,嘉琪准备完成题目“计算,计算× 的结果是等内容,欢迎下载使用。














