北师大版八年级上册第七章 平行线的证明1 为什么要证明精品教学设计

7.1 为什么要证明

【教学目标】

1.经历对命题的观察、分析、实验以及动手操作、画图、测量等过程,并对获得的数学猜想进行试验验证,体验直观判断有时不一定正确,理解证明的必要性.

2.在交流中,尝试从数学的角度运用所学的知识和方法寻求证据、给出证明,感受数学思考的合理性和严密性.

【重点难点】

●重点:感受证明的必要性.

●难点:运用所学的知识和方法寻求证据、给出证明.

【教法与学法】

●教法:结合大量的实例引入,启发、引导学生实验、观察、归纳,感受证明的必要性.

●学法:观察、讨论、合情推理及归纳应用相结合.

【教学过程】

一、情境引入

1.大家可能听说过烽火戏诸侯的故事吧,在这个故事里,诸侯认为周幽王点烽火只是为了戏弄他们,博取美人一笑,其实,这就是推理.这个推理是否是正确的呢?

2.据说哥德巴赫无意中发现,10=3+7,20=3+17,30=13+17,于是他大胆猜想:任何一个不小于6的偶数都可以表示成两个奇质数的和.这是正确的吗?至今无人证实.

3.“眼见为实”是中国的一句古话,让我们一起看看,眼见是否为实?

教材图7-1          教材图7-2

(1)如教材图7-1中两条线段的长度一样吗?教材图7-2中的四边形是正方形吗?请你先观察,再设法检验你观察到的结论.

以前我们通过观察、实验、归纳得到了很多结论.观察、实验、归纳得到的结论一定正确吗?

4.看看下面的问题,一起想一想,是否正确?

教材图7-3

如教材图7-3, 把地球看成是球形,假如用一根比地球赤道长1 m的铁丝将地球赤道围起来,铁丝与地球赤道之间的间隙能有多大?能放进一个拳头吗?先凭感觉想象一下,再具体算一算,看看与你的感觉是否一致,并与同伴进行交流.

二、互动新授

 学生积极参与活动,自主探究、互动交流,他们可能会为能否放进一个拳头争论.

 教师引导学生想一想,理由是什么?

 【实验归纳】(1)通过测量,可以得出教材图7-1中两条线段的长度相等;教材图7-2中的四边形是正方形.

 (2)如果设地球半径为R,则地球周长为2πR,则铁丝长为2πR+1,绕赤道一周,其半径为,所以铁丝半径与地球半径的差为 m,大约0.16 m,可以放进一个拳头.

 【做一做】(1)代数式n2-n+11的值是质数吗?当n=0,1,2,3,4,5试一试,你能否由此得到结论:对于所有的自然数n,n2-n+11都是质数?与同伴交流.

(2)如教材图7-4,在△ABC中,点D,E分别是AB,AC的中点,连接DE、DE与BC有怎样的位置关系和数量关系?请你先猜一猜,再设法检验你的猜想,你能肯定你的结论对所有的△ABC都成立吗?与同伴进行交流.

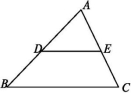教材图7-4

学生积极参与,自主探究、互动交流,为结论是否成立而争论.

 教师引导学生想一想,理由是什么?

 【议一议】实验、观察、归纳是人们认识事物的重要手段.通过实验、观察、归纳得到的结论都是正确的吗?在上面的问题中,你是怎样判断一个结论是否正确的?说说你的经验与困惑.

眼见为实,耳听为虚.事实上,跟见未必为实,我们可能被眼睛所蒙蔽.

实验、观察、归纳得到的结论可能正确,也可能不正确.因此,要判断一个数字结论是否正确,仅仅依靠实验、观察、归纳是不够的,必须进行有根有据的证明.

【设计意图】通过大量的实例,直观地感受实验、观察、归纳得到的结论可能正确,也可能不正确.理解证明的必要性.

三、例题讲解

【例1】一个两位数,它的十位数字为a,个位数字为b,若把它的十位数字与个位数字对调,将得到一个新两位数,这两个数的和能被11整除吗?差呢?我们可验证一下:比如23,对调数字后得到新两位数32,而23+32=55,32-23=9,因此我们断定,这两个数的和能被11整除,差不能被11整除.

 问上述说法正确吗?

解析:没有严格的推理,仅由若干特例归纳得出的结论可能潜藏着错误,因此要判断这两个数的和与差是否能被11整除,我们可以推理,设原两位数为10a+b,新两位数为10b+a先求10a+b与10b+a的和与差,再看这个和与差是否是11的整数倍,若是,则可整除.

【例2】已知实数a、b、c满足a=6-b,c2=ab-9,你能肯定a等于b吗?

解析:凭经验、观察或实验得到的结论未必正确.只有经过推理证明,才能判断一个结论是否正确.

四、巩固练习

1.下列推理正确的是 (　　)

A.弟弟今年13岁,哥哥比弟弟大6岁,到了明年,哥哥比弟弟只大5岁了,因为弟弟明年比今年长大了1岁

B.如果a>b,b>c,则a>c

C.∠A与∠B相等,原因是它们看起来大小也差不多

D.因为对顶角必然相等,所以相等角也必是对顶角

2.如图所示,若已知C,D是线段AB上两点,且AC=DB,E是AB中点,那么点E的位置有什么特点?你能说明原因吗?

五、课堂小结

通过本节课的学习,你有什么收获?

本节课主要学习了:

眼见未必为实,要使事实成立,必须要有根有据地证明.

【布置作业】

教材习题7.1.

【板书设计】

1　为什么要证明

1.眼见为实

2.证明的必要性

【教学反思】

作为推理证明的起始课,如何吸引学生的眼球是我们要重点解决的问题,如何培养学生的逻辑思维能力是我们今后的重点课题.一旦引起学生的兴趣.就能吸引学生进一步探究以后的内容.因此本课选用了大量的实例、图片并且可以发动学生去发现、参与探索猜想,验证猜想,激发学生的参与热情,给学生提供展示自我的时间和机会.