北师大版八年级上册2 中位数与众数公开课教学设计

教学目标

进一步理解众数和中位数的概念，能根据所给信息合理地运用相应的数据代表分析问题，体会平均数、中位数和数三者之间的差别，能选择恰当的数据代表对数据做出自己的判断

重 难 点

掌握中位数、众数等数据代表的概念。选择恰当的数据代表对数据做出判断。

教学过程

旁注与纠错

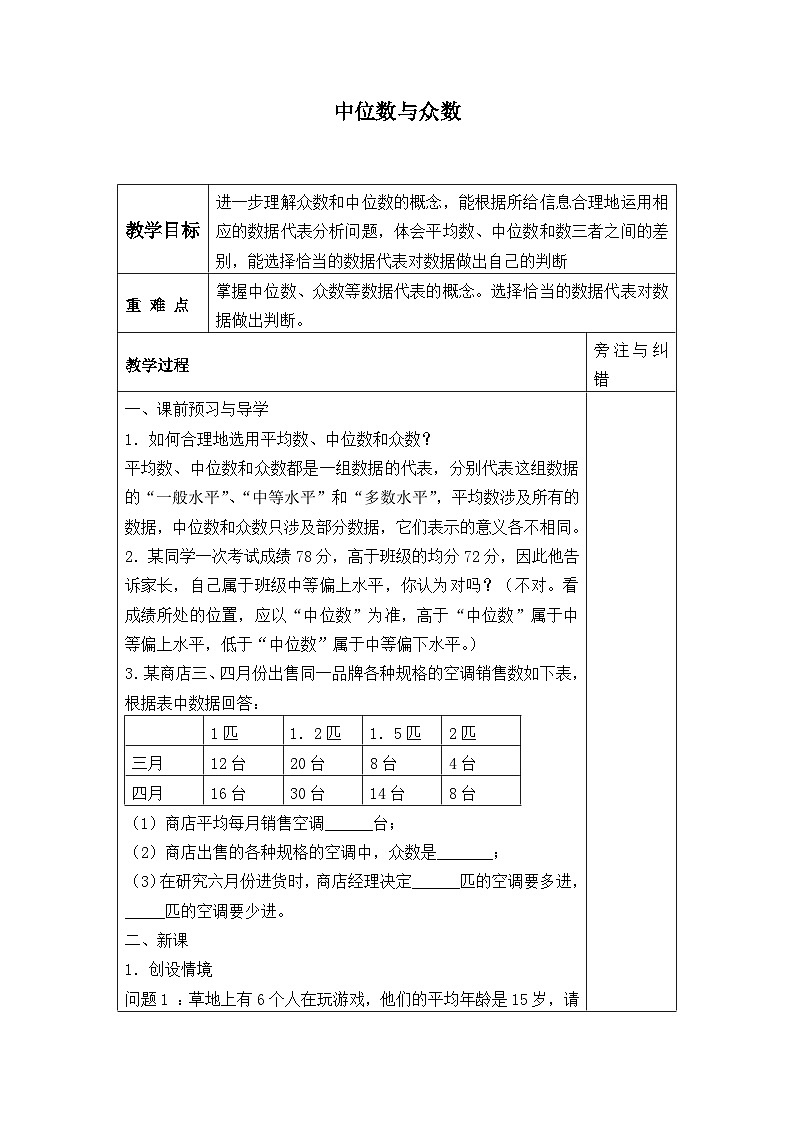
一、课前预习与导学                                     

1．如何合理地选用平均数、中位数和众数？

平均数、中位数和众数都是一组数据的代表，分别代表这组数据的“一般水平”、“中等水平”和“多数水平”，平均数涉及所有的数据，中位数和众数只涉及部分数据，它们表示的意义各不相同。

2．某同学一次考试成绩78分，高于班级的均分72分，因此他告诉家长，自己属于班级中等偏上水平，你认为对吗？（不对。看成绩所处的位置，应以“中位数”为准，高于“中位数”属于中等偏上水平，低于“中位数”属于中等偏下水平。）

3．某商店三、四月份出售同一品牌各种规格的空调销售数如下表，根据表中数据回答：

（1）商店平均每月销售空调______台；

（2）商店出售的各种规格的空调中，众数是_______；

（3）在研究六月份进货时，商店经理决定______匹的空调要多进，_____匹的空调要少进。

二、新课

1．创设情境

问题1 ：草地上有6个人在玩游戏，他们的平均年龄是15岁，请你想象一下是怎样年龄的6个人在玩游戏？

(可以都是15岁，也可以是65岁+5个5岁 ，只有平均数还不能恰当地描述这个例子)

问题2 甲、乙两班举行跳绳比赛，比赛学生的成绩经统计后得下表：

比较两班学生成绩的平均数、优秀率（大于150为优秀）的高低，（平均数

显然是一样，优秀率乙比甲高。由中位数的定义可知，甲班45个数据中由低到高排，中间的数（也就是23位）是149，而乙班中间的数是151，它后面的数肯定都大于150，这说明乙班优秀人数比甲班多，那么乙班的优秀率就比甲班高）

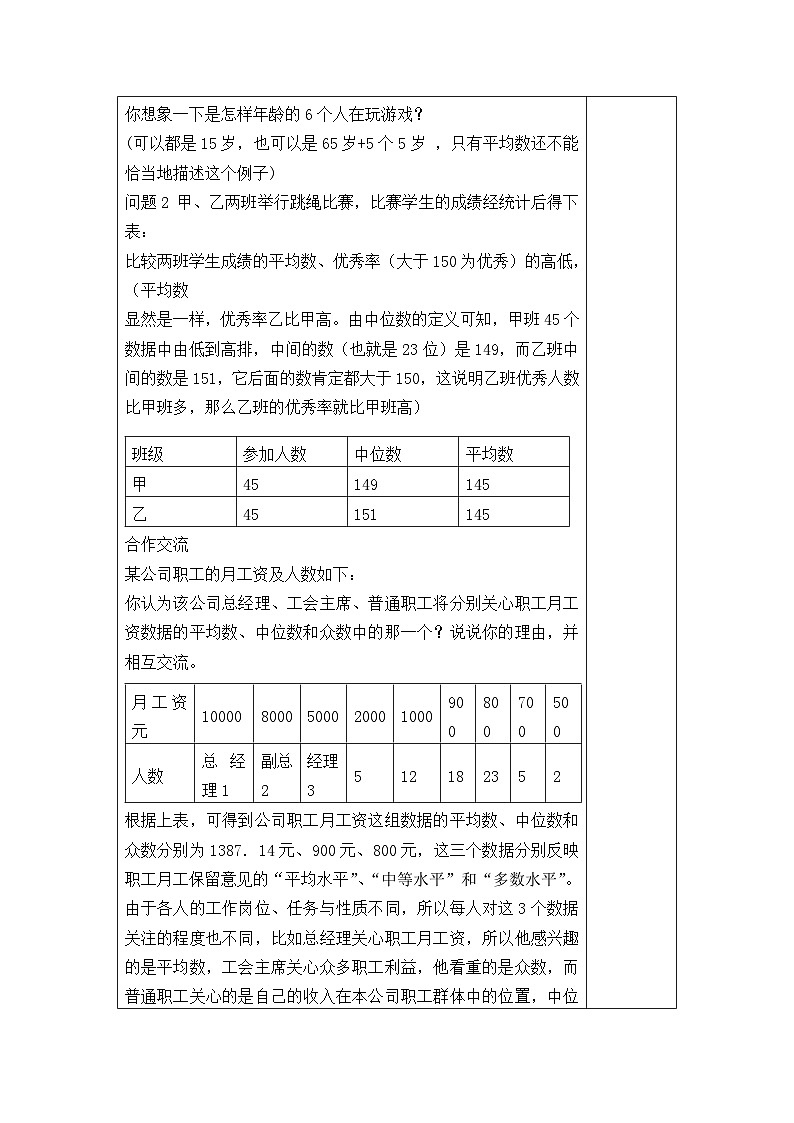
合作交流

某公司职工的月工资及人数如下：

你认为该公司总经理、工会主席、普通职工将分别关心职工月工资数据的平均数、中位数和众数中的那一个？说说你的理由，并相互交流。

根据上表，可得到公司职工月工资这组数据的平均数、中位数和众数分别为1387．14元、900元、800元，这三个数据分别反映职工月工保留意见的“平均水平”、“中等水平”和“多数水平”。由于各人的工作岗位、任务与性质不同，所以每人对这3个数据关注的程度也不同，比如总经理关心职工月工资，所以他感兴趣的是平均数，工会主席关心众多职工利益，他看重的是众数，而普通职工关心的是自己的收入在本公司职工群体中的位置，中位数能帮助职工了解自己的工资收入是“中上”还是“中下”水平。

在实际生活中针对同一份材料，同一组数据，当人们怀着不同的目的，选择不同的数据代表，从不同的角度进行分析时，看到的结果可能是截然不同的，作为信息的接受者，分析数据应从多角度对统计数据人出较全面的分析，从而避免机械的，片面的解释。

数学实验：教师捏住一根绳子的两端，将绳子拉直，面对全体学生。

请全班同学目测并估计这根绳子的长度。

将全班每位同学的估计值制成统计表和统计图，并计算全班同学估计值的平均数、中位数和众数

根据（2）中计算的结果，请你确定一个最后的估计值，作为全班同学对这根绳子长度的估计值。

三、例题讲解

例1 ：某班的教室里，三位同学正在为谁的数学成绩最好而争论，他们的五次数学成绩分别是小玲：62．94．95．98．98．小明：62．62．98．99．100 小丽：40、62．85．99．99，他们都认为自己的成绩比另两位同学的好，请你结合各组数据的三个代表，谈谈你的观点

[议一议]平均数、中位数与众数都有哪些自己的特点？

平均数：充分利用数据所提供的信息，应用最为广泛，但……

中位数：计算简单，受极端值影响较小，但……

众数：当一组数据中有些数据多次重复出现时，众数往往是人们尤为关心的一个量

四、总结反思

在实际问题中，平均数是最常用的指标，但不能一味的使用平均数来确定数据的特征，根据不同的实际需要，确定用平均数、中位数还是众数反映数据的特征。平均数、中位数、和众数各有所长，也各有其短。

用平均数作为一组数据的代表，比较可靠和稳定，它与这组数据中的每一个数都有关系，对这组数据所包含的信息的反映最为充分，因而其应用也最为广泛，特别是在进行统计推断时有最要的作用，但计算时比较繁琐，并且容易受到极端数据的影响。

用众数作为一组数据的代表，着眼于对数据出现的频数的考察，其大小只与这组数据中的部分数据有关，可靠性比较差，但众数不受极端数据的影响。当一组数据中有不少数据多次重复出现时，其众数往往是我们关心的一种统计量。

用中位数作为一组数据的代表，可靠性也比较差，但中位数也不受极端数据的影响，当一组数据中的个别数据变动较大时，可用他来描述其集中趋势。

高一级学校录取新生主要是依据考生的总分，这与平均数、中位数、众数中的哪一个关系较大？

五、课堂练习

某商场进了一批苹果，每箱苹果质量约5千克，进仓库前，从中随机抽出10箱检查，称得10箱苹果的质量如下（单位：千克）

4．8，5．0，5．1，4．8，4．9，4．8，5．1，4．9，4．7，4．7

请指出这10箱苹果质量的平均数、中位数和众数

2．某瓜农采用大棚栽培技术种植了一亩地的良种西瓜，这亩地产西瓜600个，在西瓜上市前该瓜农随机摘下了10个成熟的西瓜，称重如下：

（1）这10个西瓜质量的众数和中位数分别是　　　和　　　　；

（2）计算这10个西瓜的平均质量，并根据计算结果估计这亩地共可收获西瓜约多少千克？

3．我市部分学生参加了2004年全国初中数学竞赛决赛，并取得优异成绩。已知竞赛成绩分数都是整数，试题满分为140分，参赛学生的成绩分数分布情况如下：

请根据以上信息解答下列问题：

（1）全市共有多少人参加本次数学竞赛决赛？最低分和最高分在什么分数范围？

（2）经竞赛组委会评定，竞赛成绩在60分以上(含60分)的考生均可获得不同等级的奖励，求我市参加本次竞赛决赛考生的获奖比例；

（3）决赛成绩分数的中位数落在哪个分数段内？

（4）上表还提供了其他信息，例如：“没获奖的人数为105人”等等。请你再写出两条此表提供的信息。