湘教版七年级上册5.2 统计图优质学案设计

5．2　统　计　图

【旧知再现】

1．条形统计图：可以清楚地看出数量的__    __．

2．折线统计图：可以明显看出数量变化的__    __.

3．扇形统计图：无法从图上直接获得数量多少，但可以清楚地看见各部分所占总数的__    __．

【新知初探】

阅读教材P151【动脑筋】，P153【做一做】，你的发现是：

　制作扇形统计图的步骤：

第一步，计算__    __；

第二步，计算各部分扇形的__    __；

第三步，在同一个圆中，根据所得的__    __度数画出各个

__    __，并注明各部分的__    __及其相应的__    __．

阅读教材P154【说一说】，你发现的规律是：

各种统计图的特点：

1．扇形统计图能清楚地表示__    __．

2．条形统计图能清楚地表示出__    __．

3．折线统计图能清楚地反映__    __．

4．复式统计图能清楚地对__    __．

【图表导思】

根据问题需要选择统计图：

【质疑判断】

1．表示某病人的体温变化，可以用折线图来表示．(     )

2．可以用扇形图表示某种饮料各个成分所占的百分比．(     )

3．扇形图和条形图都能够明显的体现出各个部分的具体数值．(     )

4．同一个问题只能用一种统计图表示，不能同时用多种统计图描述数据．(     )

　制作扇形统计图

【教材P158习题5.2A组T3拓展】——扇形统计图的制作方法

　课题小组从某市20 000名九年级男生中，随机抽取了1 000名进行50米跑测试，并根据测试结果制成了统计表．

(1)a的值为________；

(2)请根据表格中的数据，绘制合理的扇形统计图．

(3)求这20 000名九年级男生中50米跑达到良好和优秀等级的总人数约为多少人？

【归纳提升】

扇形统计图的三个作用

1．反映各部分之间的大小关系及差距等．

2．当知道总体的具体数量时，可以借助扇形统计图求出各部分的具体数量．

3．当知道某一部分的具体数量时，也可借助扇形统计图求出总体的具体数量．

变式一：巩固

(2020·攀枝花中考)如图是某校参加各兴趣小组的学生人数分布扇形统计图，已知参加STEAM课程兴趣小组的人数为120人，则该校参加各兴趣小组的学生共有

__    __人．

变式二：提升 某校学生来自甲，乙，丙三个地区，其人数比为2∶7∶3，绘制成如图所示的扇形统计图，则甲地区所在扇形的圆心角度数为__    __度．

　从统计图获取信息

【教材P165复习题5B组T14拓展】——理解统计图信息

　(2020·岳阳中考)我市某学校落实立德树人根本任务，构建“五育并举”教育体系，开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程．为了解七年级学生对每类课程的选择情况，随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程)，将调查结果绘制成如图两幅不完整的统计图：

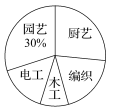
(1)本次随机调查的学生人数为________人；

(2)补全条形统计图；

(3)若该校七年级共有800名学生，请估计该校七年级学生选择“厨艺”劳动课程的人数．

【完善解答】

(1)通过条形图可以得到选择园艺的人数为__    __人从条形统计图获取信息

通过扇形统计图可以得到选择园艺的人数占总人数的__    __%

…………………………………………………从扇形统计图获取信息

设总人数为x，列方程，得：

__    __＝18 ， …………………………列方程

x＝__    __． …………………………………解方程

(2)选择编织课程的人数为：

60－__    __－18－__    __－6＝__    __(人)，

…………………………………………………各部分人数之和等于样本容量

补全条形统计图如图所示：

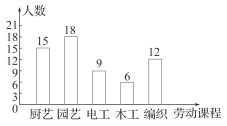
(3)800×__    __＝__    __(人).样本估计总体

答：该校七年级800名学生中选择“厨艺”劳动课程的有__    __人．

变式一：巩固 如图是某手机店1～4月的两张销售情况统计图，根据统计图，四个同学得出了以下结论，其中正确的为(     )

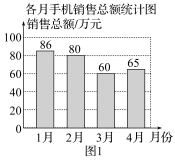
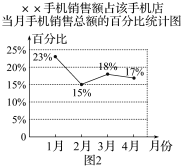
A．4月××手机销售额为60万元

B．4月××手机销售额比3月有所上升

C．3月××手机销售额比2月有所上升

D．3月与4月××手机的销售额无法比较，只能比较该店销售总额

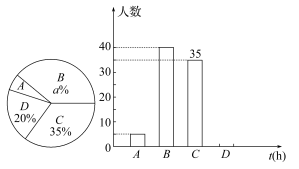
变式二：提升 (2020·娄底中考)我市开展“温馨家园，创文同行”活动，某初中学校倡议学生利用双休日进社区参加义务劳动，为了了解同学们的劳动情况，学校随机调查了部分同学的劳动时间t(h)：A.0≤t≤0.5，B.0.5＜t≤1，C.1＜t≤1.5，D.t＞1.5，将所得数据绘制成了如图不完整的统计图：

(1)本次调查参加义务劳动的学生共________人，a＝________．

(2)补全条形统计图．

(3)扇形图中“0≤t≤0.5”部分的圆心角是______度．

【归纳提升】

解决统计图综合运用问题时的“两点注意”

1．找出条形统计图和扇形统计图中表示相同含义的量，作为解题突破口．

2．掌握扇形统计图中的常用公式

(1)各部分占总体的百分比之和＝__    __．

(2)每部分数量＝__    __×该部分占总体的百分比．

(3)__    __＝每部分数量÷该部分占总体的百分比．

(4)每部分占总体的百分比＝该部分数量÷__    __．

(5)每部分占总体的百分比＝该部分对应扇形圆心角的度数÷__    __．

(6)每部分对应扇形圆心角的度数＝__    __×该部分占总体的百分比．

　统计图的选择

【教材P156例拓展】——选择统计图的方法

　近几年，随着电子商务的快速发展，“电商包裹件”占“快递件”总量的比例逐年增长，查阅企业财报，某网站得到如下统计表：

(1)请选择适当的统计图，描述2016～2019年“电商包裹件”占当年“快递件”总量的百分比(精确到1%).

(2)若2020年“快递件”总量将达到675亿件，请估计其中“电商包裹件”约为多少亿件？

【归纳提升】

统计图的特点及选用原则

变式一：巩固 要反映长沙市一周内每天的最高气温的变化情况，宜采用(     )

A．条形统计图

B．扇形统计图

C．折线统计图

D．条形图和扇形图均可以

变式二：提升 八年级的同学们即将步入初三，某主题班会小组为了了解本校八年级同学对初三的第一印象，打算抽样调查40位同学．

(1)有同学提议：“八年级1班的人数刚好是40人，不如我们直接调查1班所有同学吧”，他的建议合理吗？请说明理由．

(2)他们用问卷随机调查了40位同学(每人只能选一项)，并统计如下：

请选择一种统计图将上表中的数据描述出来．

(3)若本校八年级共有500名学生，请估计对初三第一印象是“忧喜交加”的同学人数．

【火眼金睛】

　如图是甲，乙两户居民家庭全年支出费用的扇形图，根据统计图，下面对全年食品支出费用判断正确的是(　　)

A.甲户比乙户多

B．乙户比甲户多

C．两户一样多

D．无法确定哪一户多

【一题多变】——貌似神异

1．本学期，小明一共参加了5次数学测验，成绩如表：

请你用合适的统计图把小明的数学成绩的变化趋势表示出来．

2．本学期，小明一共参加了5次数学测验，成绩如下：

请你用合适的统计图把小明的数学成绩表示出来．

【综合提升】

　为丰富学生课外活动，某校积极开展社团活动，学生可根据自己的爱好选择一项，已知该校开设的体育社团有：A：篮球，B：排球，C：足球，D：羽毛球，E：乒乓球．李老师对某班同学选择体育社团情况进行调查统计，制成了两幅不完整的统计图(如图)，则以下结论不正确的是(     )

A．选社团E的有5人

B．选社团D的扇形圆心角是72°

C．选社团A的人数是选社团B的人数的两倍

D．选社团B的扇形圆心角比选社团D的扇形圆心角的度数少21.6°