
河南省平顶山市鲁山县2022-2023学年七年级下学期期末数学试题
展开![]() 2022~2023学年下学期期末调研试卷
2022~2023学年下学期期末调研试卷
七年级数学
注意事项:
1.本试卷分试题卷和答题卡两部分,试题卷共4页,三个大题,满分120分,考试时间100分钟.
2.试题卷上不要答题,请用0.5毫米黑色签字水笔直接把答案写在答题卡上,答在试题卷上的答案无效.
3.答题前,考生务必将本人姓名、准考证号填写在答题卡第一面的指定位置.
一、选择题(每小题3分,共30分)
1.下面是小明同学搜集的一些用数学家名字命名的图形,其中是轴对称图形的是()
A.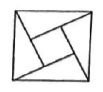 B.
B. C.
C. D.
D.
赵爽弦图费马螺线斐波那契螺旋线笛卡尔心形线
2.下列运算正确的是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列说法正确的是()
A.小明买一张体育彩票中“一等奖”是随机事件
B.任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是必然事件
C.“清明时节雨纷纷”是必然事件
D.若a是有理数,则“![]() ”是不可能事件
”是不可能事件
4.在一个暗箱里放有a个除颜色外其他完全相同的球,这a个球中只有3个红球,每次将球搅拌均匀后,任意摸出一个球,记下颜色再放回暗箱,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.25,那么可以推算出a大约是()
A.12 B.9 C.4 D.3
5.如图是婴儿车的平面示意图,其中![]() ,
,![]() ,
,![]() ,那么∠2的度数为()
,那么∠2的度数为()
A.80° B.90° C.100° D.160°
6.小明在学习完本册知识后整理了一些结论:(1)内错角的角平分线也平行;(2)直线外一点与直线上各点连接的所有线段中,垂线段最短;(3)平面内四条直线a,b,c,d,如果![]() ,
,![]() ,
,![]() ,那么
,那么![]() ;(4)有两边和第三边上的中线分别相等的两个三角形全等.其中正确的有()
;(4)有两边和第三边上的中线分别相等的两个三角形全等.其中正确的有()
A.1个 B.2个 C.3个 D.4个
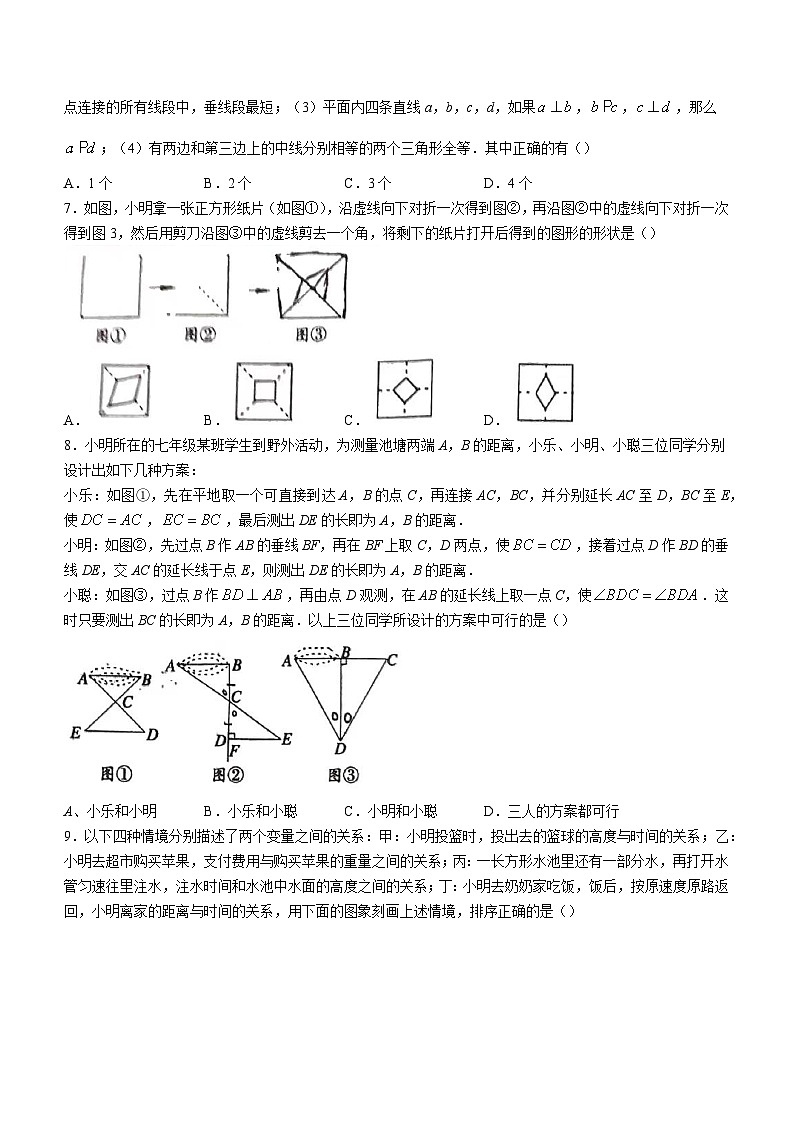
7.如图,小明拿一张正方形纸片(如图①),沿虚线向下对折一次得到图②,再沿图②中的虚线向下对折一次得到图3,然后用剪刀沿图③中的虚线剪去一个角,将剩下的纸片打开后得到的图形的形状是()

A. B.
B.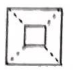 C.
C.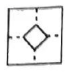 D.
D.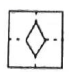
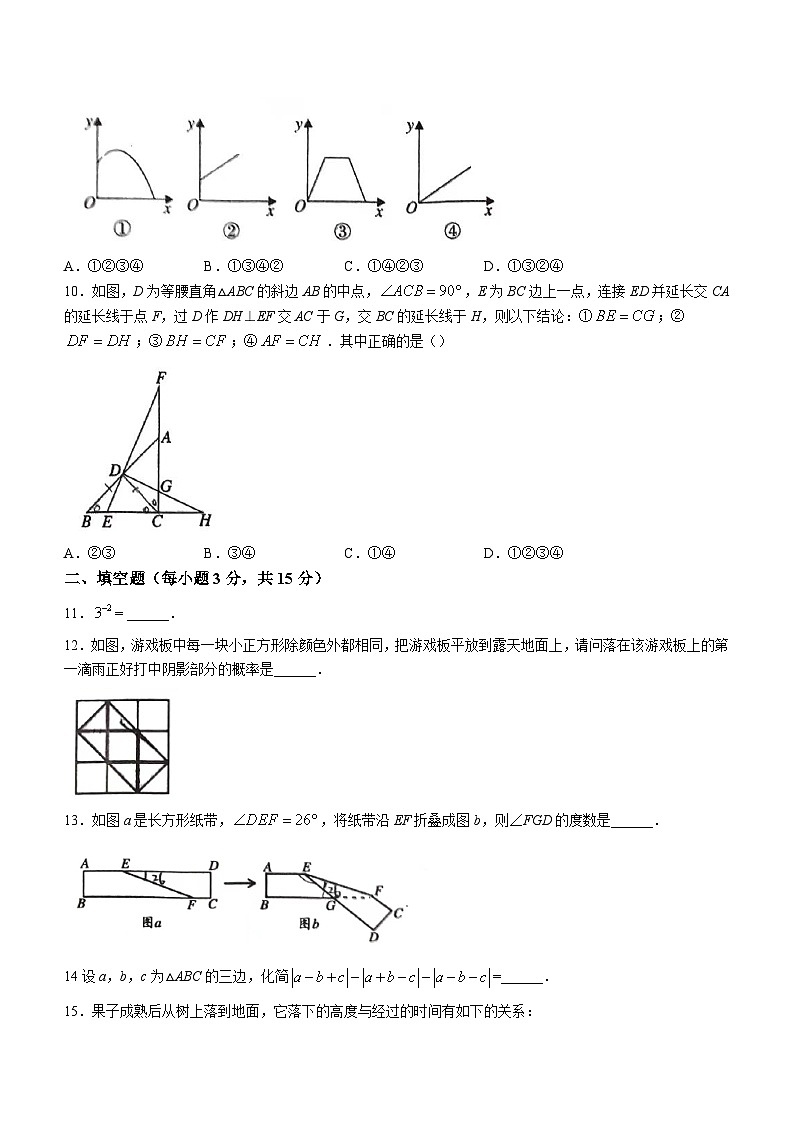
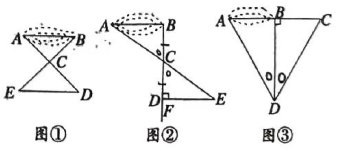
8.小明所在的七年级某班学生到野外活动,为测量池塘两端A,B的距离,小乐、小明、小聪三位同学分别设计出如下几种方案:
小乐:如图①,先在平地取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使![]() ,
,![]() ,最后测出DE的长即为A,B的距离.
,最后测出DE的长即为A,B的距离.
小明:如图②,先过点B作AB的垂线BF,再在BF上取C,D两点,使![]() ,接着过点D作BD的垂线DE,交AC的延长线于点E,则测出DE的长即为A,B的距离.
,接着过点D作BD的垂线DE,交AC的延长线于点E,则测出DE的长即为A,B的距离.
小聪:如图③,过点B作![]() ,再由点D观测,在AB的延长线上取一点C,使
,再由点D观测,在AB的延长线上取一点C,使![]() .这时只要测出BC的长即为A,B的距离.以上三位同学所设计的方案中可行的是()
.这时只要测出BC的长即为A,B的距离.以上三位同学所设计的方案中可行的是()
A、小乐和小明 B.小乐和小聪 C.小明和小聪 D.三人的方案都可行
9.以下四种情境分别描述了两个变量之间的关系:甲:小明投篮时,投出去的篮球的高度与时间的关系;乙:小明去超市购买苹果,支付费用与购买苹果的重量之间的关系;丙:一长方形水池里还有一部分水,再打开水管匀速往里注水,注水时间和水池中水面的高度之间的关系;丁:小明去奶奶家吃饭,饭后,按原速度原路返回,小明离家的距离与时间的关系,用下面的图象刻画上述情境,排序正确的是()
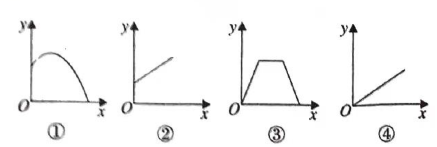
A.①②③④ B.①③④② C.①④②③ D.①③②④
10.如图,D为等腰直角△ABC的斜边AB的中点,![]() ,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G,交BC的延长线于H,则以下结论:①
,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G,交BC的延长线于H,则以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的是()
.其中正确的是()
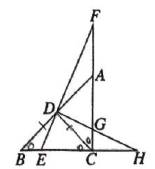
A.②③ B.③④ C.①④ D.①②③④
二、填空题(每小题3分,共15分)
11.![]() = ______.
= ______.
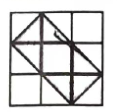
12.如图,游戏板中每一块小正方形除颜色外都相同,把游戏板平放到露天地面上,请问落在该游戏板上的第一滴雨正好打中阴影部分的概率是______.
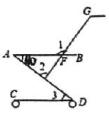
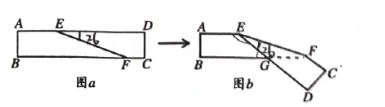
13.如图a是长方形纸带,![]() ,将纸带沿EF折叠成图b,则∠FGD的度数是______.
,将纸带沿EF折叠成图b,则∠FGD的度数是______.
14设a,b,c为△ABC的三边,化简![]() =______.
=______.
15.果子成熟后从树上落到地面,它落下的高度与经过的时间有如下的关系:
时间t(秒) | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | |
落下的高度h(米) |
|
|
|
|
|
| |
如果果子经过2秒落到地上,那么此果子开始落下时离地面的高度大约是______米.
三、解答题(共8题,75分)
16.(10分)化简:
(1)![]() ; (2)已知
; (2)已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
17.(9分)先化简,再求值:![]() .
.
其中![]() ,
,![]() .
.
18.(9分)小明发现,任意一个直角三角形都可以分割成两个等腰三角形,已知:在△ABC中,![]() .求作:直线CD,使得直线CD将△ABC分割成两个等腰三角形。下面是小明设计的尺规作图过程.
.求作:直线CD,使得直线CD将△ABC分割成两个等腰三角形。下面是小明设计的尺规作图过程.
作法:如图,①作直角边CB的垂直平分线MN,与斜边AB相交于点D;②作直线CD,则直线CD就是所求作的直线.

根据小明设计的尺规作图过程,解决下列问题:
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)小明进一步探究:以点D为圆心,适当长为半径画弧分别交DA、DC于P、Q两点,再分别以点P、Q为圆心,大于![]() 的长为半径画弧,两弧在∠ADC内交于点M,直线DM交AC于点E,则AE=CE( )(填写理由),使用尺规作图在图中补全作图痕迹.
的长为半径画弧,两弧在∠ADC内交于点M,直线DM交AC于点E,则AE=CE( )(填写理由),使用尺规作图在图中补全作图痕迹.
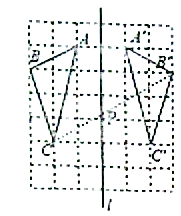
19.(9分)如图,在边长为1的小正方形组成的网格中,点A,B,C均在小正方形的顶点上.
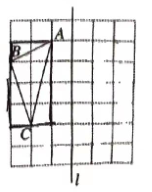
(1)在图中画出与△ABC关于直线l成轴对称的△A'B'C';
(2)在直线l上找一点P,使得△BPC的周长最小;
(3)求△A'B'C'的面积.
20.(9分)一个不透明的口袋中装有8个白球和12个红球,每个球除颜色外都相同.
(1)“从口袋里随机摸出一个球是黄球”这一事件是______事件;“一次性摸出9个球,摸到的球中至少有一个红球”这一事件发生的概率为______;
(2)求从口袋里随机摸出一个球是红球这一事件的概率;
(3)从口袋里取走x个红球后,再放入x个白球,并充分摇匀,如果随机摸出白球的概率是![]() ,求x的值.
,求x的值.
21.(9分)如图,已知点B,F,C,E在同一直线上.
(1)![]() ,(2)
,(2)![]() ,(3)
,(3)![]() ,(4)
,(4)![]() ,请自选三个作为条件,第四个作为结论,编一道数学问题,并写出解答过程.
,请自选三个作为条件,第四个作为结论,编一道数学问题,并写出解答过程.
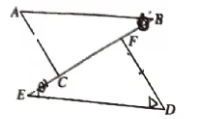
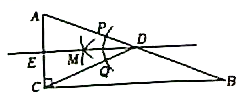
22.(10分)如图,在△ABC中,![]() ,
,![]() ,AD为BC边上的中线,过D作直线DE交直线AB于E,过D作直线
,AD为BC边上的中线,过D作直线DE交直线AB于E,过D作直线![]() ,并交直线AC于F.
,并交直线AC于F.
(1)若E点在线段AB上(非端点),则线段DE与DF的数量关系是______;
(2)若E点在线段AB的延长线上,判断此时线段DE与DF的数量关系,并说明理由.

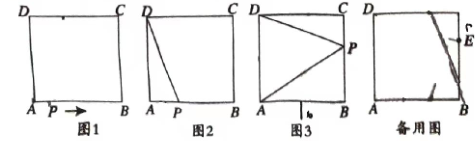
23.(10分)如图1,已知正方形ABCD的边长为16,点P为正方形ABCD边上的动点,动点P从点A出发,沿着A→B→C→D运动到D点时停止,设点P经过的路程为x,△APD的面积为y.
(1)如图2,当![]() 时,y=______;
时,y=______;
(2)如图3,当点P在边BC上运动时,y=______;
(3)当![]() 时,x=______;
时,x=______;
(4)若点E是边BC上一点且![]() ,连接DE,在正方形的边上是否存在一点P,使得△DCE与△BCP全等?若存在,求出此时x的值;若不存在,请说明理由.
,连接DE,在正方形的边上是否存在一点P,使得△DCE与△BCP全等?若存在,求出此时x的值;若不存在,请说明理由.
2022—2023学年下学期期末调研试卷参考答案
七年级数学
一、选择题(每小题3分,共30分)
1—5:DBAAB 6—10:CADCD
二、填空题(每小题3分,共15分)
11.![]() 12.
12.![]() 13.52° 14.
13.52° 14.![]() 15.20
15.20
三、解答题(共8题,75分)
16.(10分)解:(1)原式![]()
![]()
=![]()
(2)∵![]() ,
,![]()
∴![]()
![]()
![]() .
.
17.(9分)解:原式=![]()
![]()
![]() \
\
当![]() ,
,![]() 时,原式
时,原式![]()
18.(9分)解:(1)如图,直线CD即为所求:
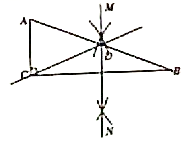
(2)三线合一;
图形如图所示:
19.(9分)解:(1)如图,![]() '即为所求;
'即为所求;
(2)如图,点P即为所求;
(3)![]() 的面积
的面积![]() .
.
20.(9分)解:(1)不可能;
(2)口袋中装有8个白球和12个红球,共有20个球,
∴从口袋中随机摸出一个球是红球的概率是![]() ;
;
(3)由题意,口袋中有(![]() )个白球和(
)个白球和(![]() )个红球,共有20个球
)个红球,共有20个球
∴从口袋中随机摸出一个球是白球的概率是![]() ,解得
,解得![]() .
.
21.(9分)本题答案不唯一,若选择(2)(3)(4)作为条件,(1)作为结论,解答过程如下:
解:如图,已知点B,F,C.E在同一直线上,![]() ,
,![]() ,
,![]() ,求证;
,求证;![]() .
.
证明:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在△ABC与△DEF,
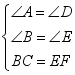 ∴
∴![]() ,
,
∴![]() .
.
22.(10分)解:(1)![]() ;
;
(2)如图2,![]() ;
;
理由如下:∵![]() ,
,![]() ,AD为BC上的中线,
,AD为BC上的中线,
∴![]() ,
,![]() ,
,![]() ,AD平分∠BAC,
,AD平分∠BAC,
∴![]() ,
,
∵![]() ∴
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
在△BDE和△ADF中,
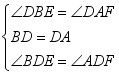 ∴
∴![]()
∴![]()
23.(10分)解:(1)32;
(2)128;
(3)3或45;
(4)当点P在边AB或边CD上运动时,存在一点P,使得△DCE与△BCP全等.
如图4,当点P在AB上时,![]() ,
,
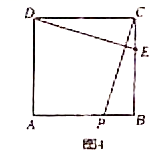
∴![]() ,∴
,∴![]() ,即
,即![]() .
.
如图5,当点P在CD上时,![]() ,
,
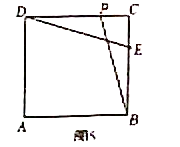
∴.![]() ,
,
∴![]() ,
,
综上所述,![]() 或38时,使得△DCE与△BCP全等.
或38时,使得△DCE与△BCP全等.
河南省平顶山市鲁山县2023-2024学年七年级上学期期末数学试题(原卷版+解析版): 这是一份河南省平顶山市鲁山县2023-2024学年七年级上学期期末数学试题(原卷版+解析版),文件包含精品解析河南省平顶山市鲁山县2023-2024学年七年级上学期期末数学试题原卷版docx、精品解析河南省平顶山市鲁山县2023-2024学年七年级上学期期末数学试题解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
河南省平顶山市鲁山县2023-2024学年七年级上学期期末数学试题: 这是一份河南省平顶山市鲁山县2023-2024学年七年级上学期期末数学试题,共10页。试卷主要包含了某航空公司规定等内容,欢迎下载使用。
河南省平顶山市鲁山县2023-2024学年九年级上学期期末数学试题: 这是一份河南省平顶山市鲁山县2023-2024学年九年级上学期期末数学试题,共10页。试卷主要包含了如图所示,在中,,若,,则,下列说法正确的是,在反比例函数等内容,欢迎下载使用。












