高考数学一轮复习夯基练习：数列的概念及简单表示法(含答案)

这是一份高考数学一轮复习夯基练习：数列的概念及简单表示法(含答案)，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
夯基练习 数列的概念及简单表示法一 、选择题1.数列{an}满足a1=1，an＋1=2an－1(n∈N*)，则a1 000=(　　)A．1         B．1 999         C．1 000         D．－1  2.对于数列{an}，“an＋1＞|an|(n=1,2，…)”是“{an}为递增数列”的(　　)A．必要不充分条件          B．充分不必要条件C．充要条件                D．既不充分也不必要条件  3.已知数列{xn}满足xn＋2=|xn＋1-xn|(n∈N*)，若x1=1，x2=a(a≤1，a≠0)，且xn＋3=xn对于任意的正整数n均成立，则数列{xn}的前2020项和S2020=(　　)A．673        B．674          C．1345           D．1347  4.在数列{an}中，a1=1，an＋1=2an＋1(n∈N*)，则a4的值为(　　)A．31　       B．30          C．15            D．63  5.某种细菌在培养过程中，每20分钟分裂一次(1个分裂为2个)．经过3小时，这种细菌由1个可繁殖成(　　)A．511个         B．512个         C．1 023个         D．1 024个  6.已知数列{an}的通项公式是an=n2＋kn＋2，若对所有的n∈N*，都有an＋1＞an成立，则实数k的取值范围是(　　)A．(0，＋∞)        B．(－1，＋∞)      C．(－2，＋∞)       D．(－3，＋∞)  7.数列{an}中,an=,则该数列前100项中的最大项与最小项分别是(　　)A.a1,a50                                  B.a1,a44                  C.a45,a44                                 D.a45,a508.数列{an}定义如下:a1=1,当n≥2时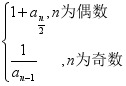,an=，若an=,则n的值为(　　)A.7                          B.8                          C.9                         D.109.数列{an}满足：a1=1，且对任意的m，n∈N*，都有am＋n=am＋an＋mn，则＋＋＋…＋=(　　)A．         B．        C．         D．  10.在数列{an}中,a1=2,an+1=an+ln(1+),则an=(　　)A.2+ln n                                     B.2+(n-1)ln n          C.2+nln n                        D.1+n+ln n 11.　能力提升练11．意大利著名数学家斐波那契在研究兔子的繁殖问题时，发现有这样的一列数：1,1,2,3,5,8，…，该数列的特点是：前两个数均为1，从第三个数起，每一个数都等于它前面两个数的和．人们把这样的一列数组成的数列{an}称为斐波那契数列．则(a1a3＋a2a4＋a3a5＋a4a6＋a5a7＋a6a8)－(a＋a＋a＋a＋a＋a)=(　　)A．0            B．－1         C．1            D．2  12.已知数列{an}满足an=(n∈N*)，将数列{an}中的整数项按原来的顺序组成新数列{bn}，则b2 019的末位数字为(　　)A．8           B．2          C．3           D．7   二 、填空题13.对于数列{an}，定义数列{bn}满足：bn=an＋1-an(n∈N*)，且bn＋1-bn=1(n∈N*)，a3=1，a4=-1，则a1=________．  14.已知a1=2,an+1-an=2n+1(n∈N*),则an=　　　　. 15.数列－1，，－，，…的一个通项公式为________. 16.在数列{an}中，a1=1，a1＋＋＋…＋=an(n∈N*)，则数列{an}的通项公式an=________.   三 、解答题17.已知数列{an}中，an=1＋(n∈N*，a∈R，且a≠0)．(1)若a=-7，求数列{an}中的最大项和最小项的值；(2)若对任意的n∈N*，都有an≤a6成立，求a的取值范围．                18.已知数列{an}的通项公式是an=n2+kn+4.(1)若k=-5,则数列中有多少项是负数?n为何值时,an有最小值?并求出最小值;(2)对任意的n∈N*,都有an+1>an,求实数k的取值范围.   19.已知数列{an}满足a1=，且当n>1，n∈N*时，有，设bn=，n∈N*.(1)求证：数列{bn}为等差数列．(2)试问a1a2是否是数列{an}中的项？如果是，是第几项； 如果不是，请说明理由．       20.已知{an}是公差为d的等差数列，它的前n项和为Sn，S4=2S2＋4，数列{bn}中，bn=.(1)求公差d的值；(2)若a1=－，求数列{bn}中的最大项和最小项的值；(3)若对任意的n∈N*，都有bn≤b8成立，求a1的取值范围．               
参考答案1.答案为：A；解析：a1=1，a2=2×1－1=1，a3=2×1－1=1，a4=2×1－1=1，…，可知an=1(n∈N*)，∴a1 000=1.  2.答案为：B.当an＋1＞|an|(n=1,2，…)时，∵|an|≥an，∴an＋1＞an，∴{an}为递增数列．当{an}为递增数列时，若该数列为－2,0,1，则a2＞|a1|不成立，即an＋1＞|an|(n=1,2，…)不一定成立．综上知，“an＋1＞|an|(n=1,2，…)”是“{an}为递增数列”的充分不必要条件．  3.答案为：D；解析：∵x1=1，x2=a(a≤1，a≠0)，∴x3=|x2-x1|=|a-1|=1-a，∴x1＋x2＋x3=1＋a＋(1-a)=2，又xn＋3=xn对于任意的正整数n均成立，∴数列{xn}的周期为3，∴数列{xn}的前2020项和S2020=S673×3＋1=673×2＋1=1347．故选D．  4.答案为：C；  5.答案为：B；解析：3小时含9个20分钟，分裂9次后细菌个数为29=512.  6.答案为：D.an＋1＞an，即(n＋1)2＋k(n＋1)＋2＞n2＋kn＋2，则k＞－(2n＋1)对所有的n∈N*都成立，而当n=1时，－(2n＋1)取得最大值－3，所以k＞－3.  7.答案为：C； 8.答案为：C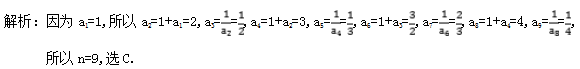； 9.答案为：D；解析：∵a1=1，且对任意的m，n∈N*都有am＋n=am＋an＋mn，∴an＋1=an＋n＋1，即an＋1-an=n＋1，用累加法可得an=a1＋=，∴==2-，∴＋＋＋…＋=21-＋-＋…＋-=，故选D．  10.答案为：A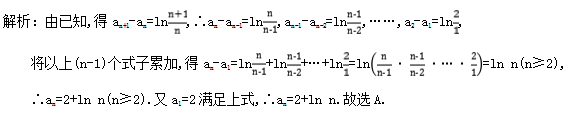； 11.答案为：A.a1a3－a=1×2－1=1，a2a4－a=1×3－22=－1，a3a5－a=2×5－32=1，a4a6－a=3×8－52=－1，…，则(a1a3＋a2a4＋a3a5＋a4a6＋a5a7＋a6a8)－(a＋a＋a＋a＋a＋a)=0.  12.答案为：D；解析：由an=(n∈N*)，可得此数列为，，，，，，，，，，，，，…，{an}中的整数项为，，，，，，…，∴数列{bn}的各项依次为2,3,7,8,12,13,17,18，…，末位数字分别是2,3,7,8,2,3,7,8，….∵2 019=4×504＋3，故b2 019的末位数字为7.故选D.   二 、填空题13.答案为：8；解析：由bn＋1-bn=1知数列{bn}是公差为1的等差数列，又b3=a4-a3=-2，所以b1=-4，b2=-3，b1＋b2=(a2-a1)＋(a3-a2)=a3-a1=-7，解得a1=8．  14.答案为：n2+1；15.答案为：an=(－1)n16.答案为：；解析：由a1＋＋＋…＋=an(n∈N*)知，当n≥2时，a1＋＋＋…＋=an－1，∴=an－an－1，即an=an－1，∴an=…=2a1=2，∴an=.   三 、解答题17.解：(1)∵an=1＋(n∈N*，a∈R，且a≠0)，a=-7，∴an=1＋(n∈N*)．结合函数f(x)=1＋的单调性，可知1>a1>a2>a3>a4，a5>a6>a7>…>an>1(n∈N*)．∴数列{an}中的最大项为a5=2，最小项为a4=0．(2)an=1＋=1＋．∵对任意的n∈N*，都有an≤a6成立，结合函数f(x)=1＋的单调性，∴5<<6，∴-10<a<-8．  18.解： 19. (1)证明:当n>1，n∈N*时，-2=2+-=4.⇔bn－bn－1=4，且b1==5.∴{bn}是等差数列，且公差为4，首项为5.(2)解:由(1)知bn=b1＋(n－1)d=5＋4(n－1)=4n＋1.∴an==，n∈N*.∴a1=，a2=，∴a1a2=.令an==，∴n=11.即a1a2=a11，∴a1a2是数列{an}中的项，是第11项．  20.解：(1)∵S4=2S2＋4，∴4a1＋d=2(2a1＋d)＋4，解得d=1.(2)∵a1=－，∴数列{an}的通项公式为an=－＋(n－1)=n－，∴bn=1＋=1＋.∵函数f(x)=1＋在和上分别是单调减函数，∴b3＜b2＜b1＜1，当n≥4时，1＜bn≤b4，∴数列{bn}中的最大项是b4=3，最小项是b3=－1.(3)由bn=1＋，得bn=1＋.又函数f(x)=1＋在(－∞，1－a1)和(1－a1，＋∞)上分别是单调减函数，且x＜1－a1时，y＜1；当x＞1－a1时，y＞1.∵对任意的n∈N*，都有bn≤b8，∴7＜1－a1＜8，∴－7＜a1＜－6，∴a1的取值范围是(－7，－6)．