


还剩22页未读,
继续阅读
所属成套资源:2023新版冀教版九年级数学上册全一册上课课件
成套系列资料,整套一键下载
2023九年级数学上册第28章圆全章综合检测上课课件新版冀教版
展开
这是一份2023九年级数学上册第28章圆全章综合检测上课课件新版冀教版,共30页。
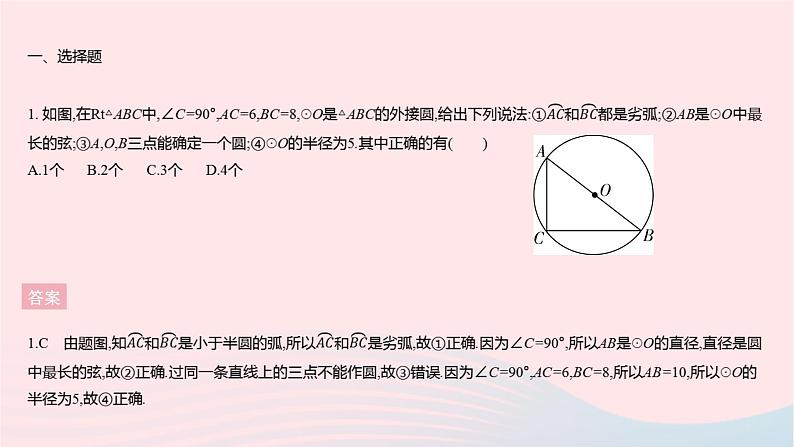
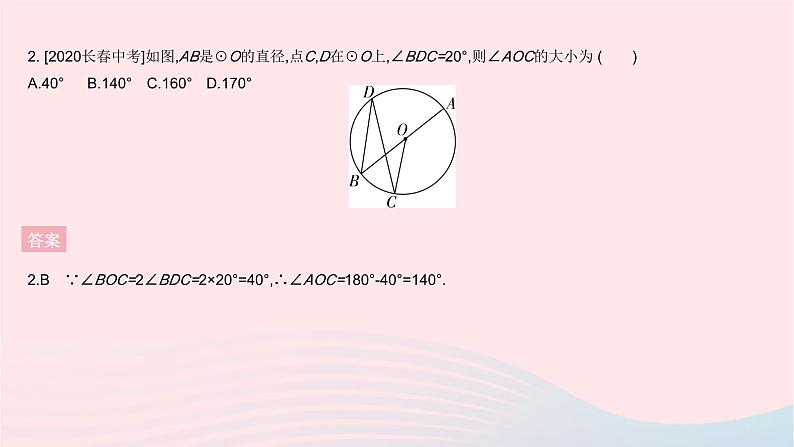
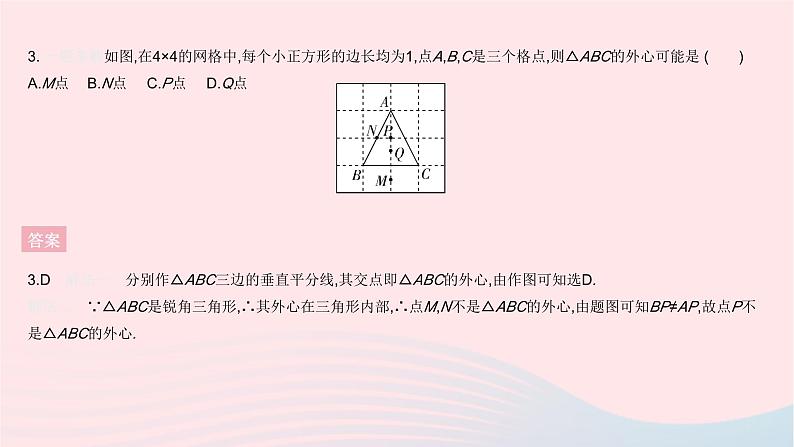
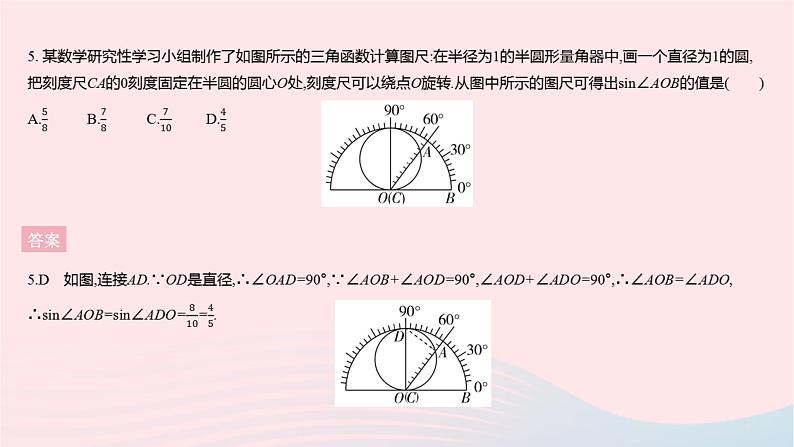
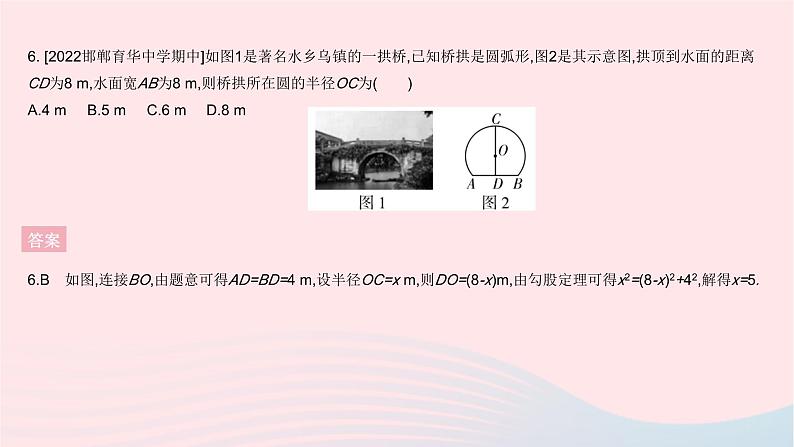
全章综合检测 答案 2. [2020长春中考]如图,AB是☉O的直径,点C,D在☉O上,∠BDC=20°,则∠AOC的大小为 ( )A.40° B.140° C.160° D.170°答案2.B ∵∠BOC=2∠BDC=2×20°=40°,∴∠AOC=180°-40°=140°.3. 一题多解如图,在4×4的网格中,每个小正方形的边长均为1,点A,B,C是三个格点,则△ABC的外心可能是 ( )A.M点 B.N点 C.P点 D.Q点答案3.D 解法一 分别作△ABC三边的垂直平分线,其交点即△ABC的外心,由作图可知选D.解法二 ∵△ABC是锐角三角形,∴其外心在三角形内部,∴点M,N不是△ABC的外心,由题图可知BP≠AP,故点P不是△ABC的外心. 答案 答案 6. [2022邯郸育华中学期中]如图1是著名水乡乌镇的一拱桥,已知桥拱是圆弧形,图2是其示意图,拱顶到水面的距离CD为8 m,水面宽AB为8 m,则桥拱所在圆的半径OC为( )A.4 m B.5 m C.6 m D.8 m答案6.B 如图,连接BO,由题意可得AD=BD=4 m,设半径OC=x m,则DO=(8-x)m,由勾股定理可得x2=(8-x)2+42,解得x=5. 答案 答案 答案 答案 答案 答案 二、填空题13. 如图,四边形ABCD为☉O的内接四边形,∠A=100°,则∠DCE的度数为 . 答案13.100° ∵四边形ABCD为☉O的内接四边形,∴∠DCB+∠A=180°,又∵∠DCB+∠DCE=180°,∴∠DCE=∠A=100°. 答案 15. 如图,四边形OBCD的顶点都在正方形网格坐标系的格点上,已知O(0,0),B(0,2),C(3,3),D(4,0).(1)四边形OBCD的外接圆的圆心M的坐标是 ; (2)这个圆中弦BC所对的圆周角的度数是 . 答案 答案 答案 答案 答案 答案 (3)解:①如图2,连接CF.∵∠BEC是△ABC中∠BAC的遥望角,∴∠BAC=2∠BEC.∵∠BFC=∠BAC,∴∠BFC=2∠BEC.∵∠BFC=∠BEC+∠FCE,∴∠BEC=∠FCE.∵∠FCE=∠FAD,∴∠BEC=∠FAD.又∵∠FDE=∠FDA,FD=FD,∴△FDE≌△FDA,∴DE=AD,∴∠AED=∠DAE.∵AC是☉O的直径,∴∠ADC=90°,∴∠AED+∠DAE=90°,∴∠AED=∠DAE=45°.
全章综合检测 答案 2. [2020长春中考]如图,AB是☉O的直径,点C,D在☉O上,∠BDC=20°,则∠AOC的大小为 ( )A.40° B.140° C.160° D.170°答案2.B ∵∠BOC=2∠BDC=2×20°=40°,∴∠AOC=180°-40°=140°.3. 一题多解如图,在4×4的网格中,每个小正方形的边长均为1,点A,B,C是三个格点,则△ABC的外心可能是 ( )A.M点 B.N点 C.P点 D.Q点答案3.D 解法一 分别作△ABC三边的垂直平分线,其交点即△ABC的外心,由作图可知选D.解法二 ∵△ABC是锐角三角形,∴其外心在三角形内部,∴点M,N不是△ABC的外心,由题图可知BP≠AP,故点P不是△ABC的外心. 答案 答案 6. [2022邯郸育华中学期中]如图1是著名水乡乌镇的一拱桥,已知桥拱是圆弧形,图2是其示意图,拱顶到水面的距离CD为8 m,水面宽AB为8 m,则桥拱所在圆的半径OC为( )A.4 m B.5 m C.6 m D.8 m答案6.B 如图,连接BO,由题意可得AD=BD=4 m,设半径OC=x m,则DO=(8-x)m,由勾股定理可得x2=(8-x)2+42,解得x=5. 答案 答案 答案 答案 答案 答案 二、填空题13. 如图,四边形ABCD为☉O的内接四边形,∠A=100°,则∠DCE的度数为 . 答案13.100° ∵四边形ABCD为☉O的内接四边形,∴∠DCB+∠A=180°,又∵∠DCB+∠DCE=180°,∴∠DCE=∠A=100°. 答案 15. 如图,四边形OBCD的顶点都在正方形网格坐标系的格点上,已知O(0,0),B(0,2),C(3,3),D(4,0).(1)四边形OBCD的外接圆的圆心M的坐标是 ; (2)这个圆中弦BC所对的圆周角的度数是 . 答案 答案 答案 答案 答案 答案 (3)解:①如图2,连接CF.∵∠BEC是△ABC中∠BAC的遥望角,∴∠BAC=2∠BEC.∵∠BFC=∠BAC,∴∠BFC=2∠BEC.∵∠BFC=∠BEC+∠FCE,∴∠BEC=∠FCE.∵∠FCE=∠FAD,∴∠BEC=∠FAD.又∵∠FDE=∠FDA,FD=FD,∴△FDE≌△FDA,∴DE=AD,∴∠AED=∠DAE.∵AC是☉O的直径,∴∠ADC=90°,∴∠AED+∠DAE=90°,∴∠AED=∠DAE=45°.
相关资料
更多









