初中数学人教版九年级上册22.3 实际问题与二次函数图文课件ppt

这是一份初中数学人教版九年级上册22.3 实际问题与二次函数图文课件ppt，共27页。PPT课件主要包含了导入新课，情景引入，讲授新课，合作探究，最小值，最大值，∵0≤3≤6，典例精析，方法归纳，矩形面积长×宽等内容，欢迎下载使用。

将一个物体抛向空中，时间与高度将成二次函数关系，那么你想知道该物体最多可以抛多高吗？
写出下列抛物线的开口方向、对称轴和顶点坐标，并写出其最值.(1) y = x2 − 4x − 5；(配方法) (2) y = −x2 − 3x + 4. (公式法)
解：(1) 开口方向：向上；对称轴：直线 x = 2； 顶点坐标：(2，-9)；最小值：-9.
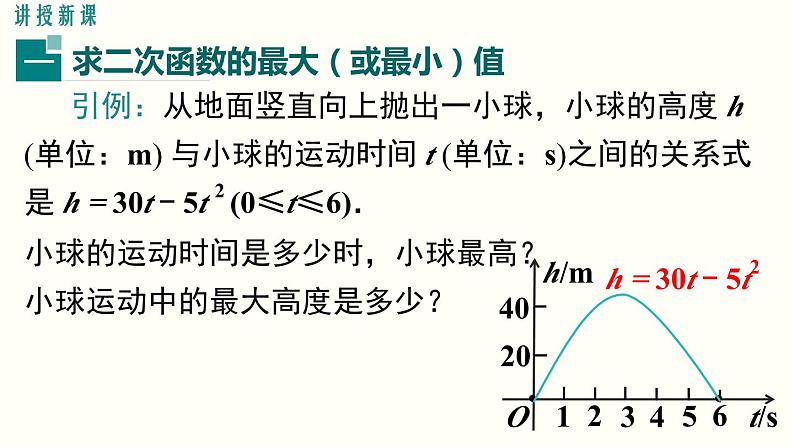
引例：从地面竖直向上抛出一小球，小球的高度 h (单位：m) 与小球的运动时间 t (单位：s)之间的关系式是 h = 30t - 5t 2 (0≤t≤6)．小球的运动时间是多少时，小球最高？小球运动中的最大高度是多少？
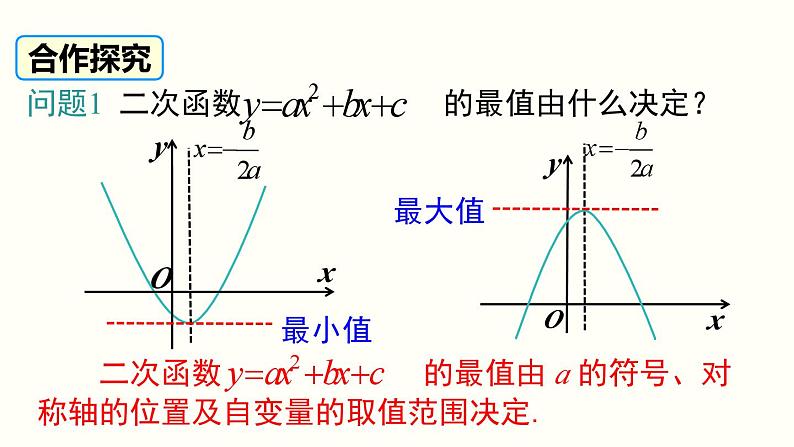
问题2 当自变量 x 为全体实数时，二次函数 y = ax2 + bx + c 的最值是多少？
问题3 当自变量 x 限定范围时，二次函数 y = ax2 + bx + c 的最值如何确定？
先判断 是否在限定范围内，若在，则二次函数在 x = 时取得一个最值，另一个最值需考察限定范围的端点处来决定；若不在，则根据二次函数的增减性确定其最值.
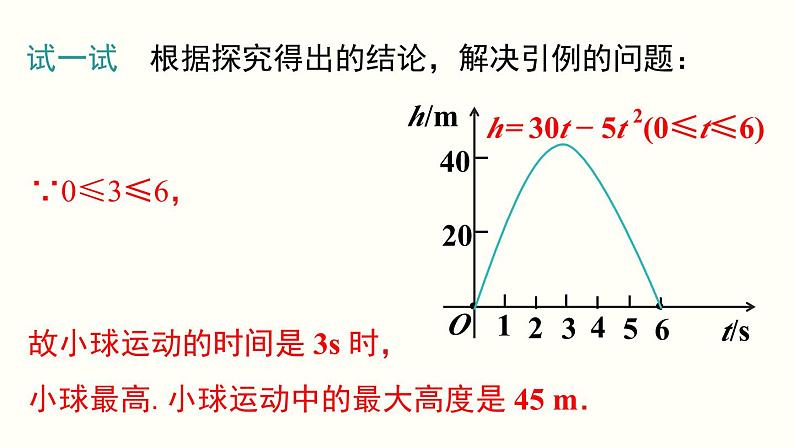
故小球运动的时间是 3s 时， 小球最高.小球运动中的最大高度是 45 m．
试一试 根据探究得出的结论，解决引例的问题：
例1 求下列函数的最大值与最小值：
∴ 当 -3≤x≤1 时 y 随着 x 的增大而减小.
1. 配方，求二次函数的顶点坐标及对称轴；
2. 画出函数图象，标明对称轴，并在横坐标上标明 x 的取值范围；
3. 判断，判断 x 的取值范围与对称轴的位置关系，根据二次函数的性质及图象，确定当 x 取何值时函数有最大或最小值，然后根据 x 的值，求出函数的最值.
例2 用总长为 60 m 的篱笆围成矩形场地，矩形面积 S (m2) 随矩形一边长 l (m) 的变化而变化. 当 l 是多少米时，场地的面积 S 最大？
问题1 矩形面积公式是什么？
问题2 如何用 l 表示另一边？
问题3 面积 S 的函数关系式是什么？
另一边长为 (30 − l) m
S = (30−l)l = −l2+30l
问题4 当 l 是多少米时，场地的面积 S 最大？
S = l (30 - l)，
即 S = -l2 + 30l (0＜l＜30).
也就是说，当 l 是 15 m 时，场地的面积 S 最大.
变式 如图，用一段长为 60 m 的篱笆围成一个一边靠墙的矩形菜园.
(1) 当墙长 32 m 时，这个矩形的长、宽 各为多少时，菜园的面积最大？最大 面积是多少？
分析：设垂直于墙的一边长为 x m，则平行于墙的边长为__________m.
矩形菜园的面积 S =______________________.
想一想 如何求得自变量 x 的取值范围？墙长 32 m 对此题有什么作用？
0＜60−2x≤32，即 14≤x＜30.
x(60 − 2x)＝ −2x2＋60x
∴ 当 x = 15 m 时，S 取最大值，此时 S最大值 = 450 m2.
解：设垂直于墙的一边长为 x m，则平行于墙的边长为 (60 − 2x) m.
∴ S = x(60 − 2x) = −2x2＋60x.
∵ S = −2x2＋60x = −2(x − 15)2 + 450，
由题意得 0＜60−2x≤32，即 14≤x＜30.
(2) 当墙长 18 m 时，这个矩形的长、宽各为多少时，菜 园的面积最大？最大面积是多少？
解：设垂直于墙的一边长为 x m，
由 (1) 知S = −2x2＋60x = −2(x2 − 30x) = −2(x − 15)2 + 450.
问题1 与(1)有什么区别？
试一试 在 (2) 中，求自变量的取值范围.
可利用的墙的长度不一样
问题2 当 21≤ x＜30 时，S 的值随 x 的增大如何变化？当 x 取何值时，S 取得最大值？
当 21≤ x＜30 时，S 随 x 的增大而减小，
故当 x = 21 时，S 取得最大值，
此时 S最大值 = −2×(21 − 15)2 + 450 = 378 (m2).
例3 用长为 6 米的铝合金材料做一个形状如图所示的矩形窗框. 窗框的高与宽各为多少时，它的透光面积最大？最大透光面积是多少？（铝合金型材宽度不计）
矩形窗框的透光面积 y 与 x 之间的函数关系式是
所以，当 x = 1 时，函数取得最大值，y最大值 = 1.5.
因此，所做矩形窗框的宽为 1 m、高为 1.5 m 时，它的透光面积最大，最大面积是 1.5 m2.
二次函数解决几何面积最值问题的方法
1. 求出函数解析式和自变量的取值范围；2. 当自变量的取值范围没有限制时，可直接利用公式 求它的最大值或最小值；3. 当自变量的取值范围有所限制时，可先配成顶点式， 然后画出函数图象的草图，再结合图象和自变量的 范围求函数最值.
1. 二次函数 y = (x + 1)2 − 2 的最小值是（ ） A．−2 B．−1 C．1 D．2
2. 二次函数 y = −2x2 − 4x + 3 (x≤−2) 的最大值为____.
3. 已知直角三角形的两直角边之和为 8，则该三角形 的面积的最大值是______.
4. 某小区要在一块空地上修建一个矩形绿化带 ABCD，绿化带一边靠墙 (墙长 25 m)，另三边用总长为 40 m 的栅栏围住．设绿化带的边长 BC 为 x m，绿化带的面积为 y m2．(1) 求 y 与 x 之间的函数关系式，并写出自变量的取值范围.
解：∵ BC = x m，
(2) 当 x 为何值时，满足条件的绿化带的面积最大？
∴ 当 x = 20 时，绿化带的面积取得最大值，最大面积为 200 m2.
5. 某广告公司设计一幅周长为 12 m 的矩形广告牌，广告设计费用每平方米 1000 元，设矩形的一边长为 x (m)，面积为 S (m2). (1)写出 S 与 x 之间的关系式，并写出自变量 x 的取值 范围；
解：由于矩形周长为 12 m，一边长为 x m，故另一边长为 (6 - x) m.
∴ S = x(6 - x) = -x2 + 6x，其中 0＜x＜6.
解：S = -x2 + 6x = -(x - 3)2 + 9 (0＜x＜6).
∴当 x = 3，即矩形的一边长为 3 m 时，其面积最大，为 9 m2.
这时设计费最多，为 9×1000 = 9000（元）.
(2) 请你设计一个方案，使获得的设计费最多，并求出这个费用.
6. 如图，在△ABC 中，∠B = 90°，AB = 12 cm，BC = 24 cm，动点 P 从点 A 开始沿 AB 向 B 以 2 cm/s 的速度移动 (不与点 B 重合)，动点 Q 从点 B 开始沿 BC 以 4 cm/s 的速度移动 (不与点 C 重合). 如果 P、Q 分别从 A、B 同时出发，那么经过 s，四边形 APQC 的面积最小.