

2022-2023学年山东省济宁市梁山县七年级(下)期末数学试卷(含解析)
展开2022-2023学年山东省济宁市梁山县七年级(下)期末数学试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 在3.14,−17, 5,0这四个数中,属于无理数的是( )
A. 3.14 B. −17 C. 5 D. 0
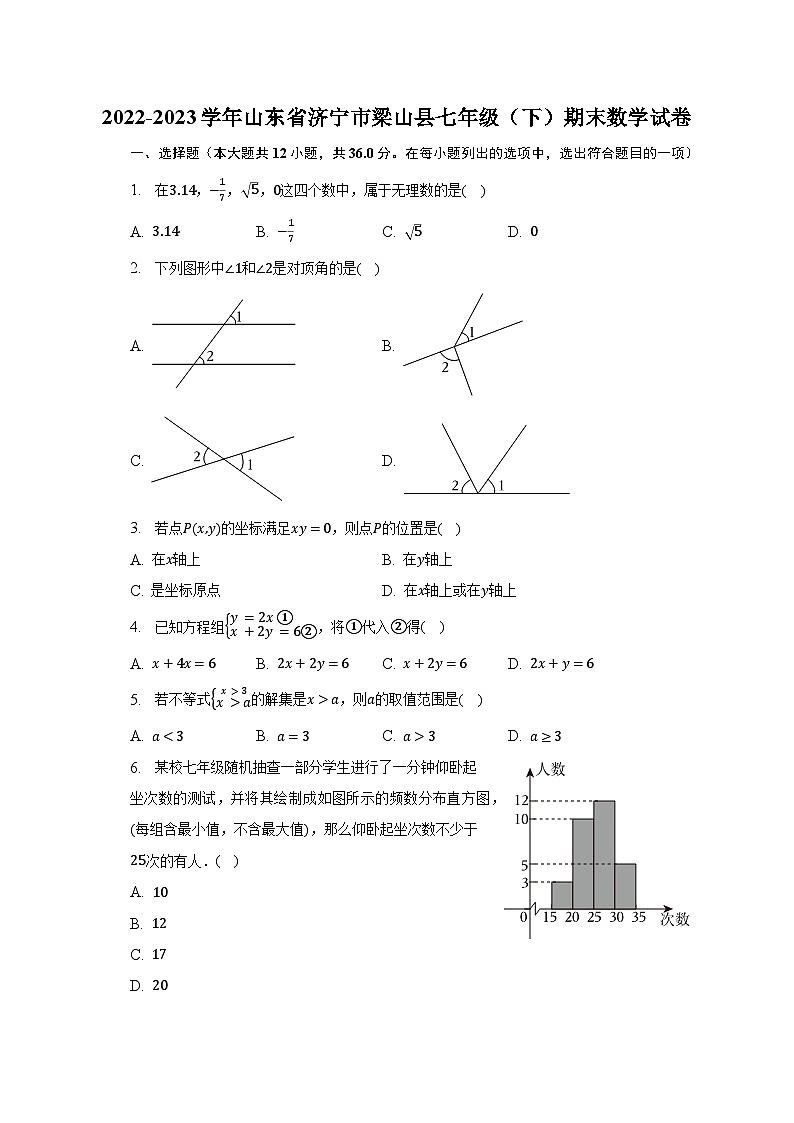
2. 下列图形中∠1和∠2是对顶角的是( )
A. B.
C. D.
3. 若点P(x,y)的坐标满足xy=0,则点P的位置是( )
A. 在x轴上 B. 在y轴上
C. 是坐标原点 D. 在x轴上或在y轴上
4. 已知方程组y=2x①x+2y=6②,将①代入②得( )
A. x+4x=6 B. 2x+2y=6 C. x+2y=6 D. 2x+y=6
5. 若不等式x>ax>3的解集是x>a,则a的取值范围是( )
A. a<3 B. a=3 C. a>3 D. a≥3
6. 某校七年级随机抽查一部分学生进行了一分钟仰卧起坐次数的测试,并将其绘制成如图所示的频数分布直方图,(每组含最小值,不含最大值),那么仰卧起坐次数不少于25次的有人.( )
A. 10
B. 12
C. 17
D. 20
7. 将不等式组x>2x≥3的解集表示在数轴上,正确的是( )
A. B.
C. D.
8. 在平面直角坐标系中,点P(−3,−5)关于x轴对称的点的坐标是( )
A. (3,−5) B. (−3,−5) C. (3,5) D. (−3,5)
9. 将一把直尺与一块直角三角板按如图所示的方式放置,若∠1=125°,则∠2的度数为( )
A. 35° B. 40° C. 45° D. 55°
10. 图①,图②都是由8个一样的小长方形拼成的,且图②中的阴影部分(正方形)的面积为1,设每块小长方形地砖的长为x cm,宽为y cm,下列方程组正确的是( )
A. 3x=5y2y−x=1 B. 3x=5y2x−y=1 C. 3y=5x2y−x=1 D. 3y=5x2x−y=1
11. 已知方程组a1x+b1y=c1a2x+b2y=c2的解是x=3y=4,则方程组3a1x+2b1y=5c13a2x+2b2y=5c2的解是( )
A. x=1y=2 B. x=3y=4 C. x=10y=103 D. x=5y=10
12. 如图,已知A1(1,2),A2(2,2),A3(3,0),A4(4,−2),A5(5,−2),A6(6,0)…,按这样的规律,则点A2022的坐标为( )
A. (2022,0) B. (2023,0) C. (2022,−2) D. (2022,2)
二、填空题(本大题共6小题,共18.0分)
13. 一个正数a的平方根分别是m和−3m+1,则这个正数a为______.
14. 某检测收集到40个数据,其中最大值为35,最小值为14,画频数分布直方图时,如果取组距为4,那么应分成______ 组.
15. 5 ______ π(填“>”“<”“=”).
16. 如图,直线a,b被c所截,∠1=130°,当∠2= ______ °时,a//b.
17. 如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(−2,1)和B(−2,−3),那么第一架轰炸机C的平面坐标是______.
18. 定义:对于实数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[5]=5,[−π]=−4.如果[x2]=−3,则x的取值范围为______ .
三、解答题(本大题共8小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
19. (本小题9.0分)
如图,a、b、c是数轴上三个点A、B、C所对应的实数.试化简: c2−|a−b|+3(a+b)3+|b−c|.
20. (本小题8.0分)
解下列方程组:
(1)x−y=42x+y=5;
(2)2x−3y=3x+2y=−2.
21. (本小题7.0分)
解不等式:解不等式组:2x−1<73x−12≥x+1,并把它的解集在数轴上表示出来.
22. (本小题7.0分)
如图所示,AB//CD,∠1=∠2,试说明∠E=∠F.
23. (本小题8.0分)
已知三角形A1B1C1是由三角形ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如表所示:
三角形ABC
A(1,0)
B(5,0)
C(6,5)
三角形A1B1C1
A1(4,2)
B1(8,b)
C1(c,7)
(1)观察表中各对应点坐标的变化,并填空:b=______,c=______;
(2)在如图的平面直角坐标系中画出三角形A1B1C1;
(3)观察平移前后各对应点之间的关系,若P(m,n)为三角形ABC中任意一点,则平移后的对应点P1的坐标为______.
24. (本小题10.0分)
某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别
正确字数x
人数
A
0≤x<8
10
B
8≤x<16
15
C
16≤x<24
25
D
24≤x<32
m
E
32≤x<40
20
根据以上信息解决下列问题:
(1)在统计表中,m= ______ ,n= ______ ,并补全直方图;
(2)扇形统计图中“E组”所对应的圆心角的度数是______ °;
(3)若该校共有964名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
25. (本小题9.0分)
如图,已知直线AB//CD,直线MN分别交AB,CD于点O,E,OF⊥OE于O,EF平分∠OED,EF与OF相交于点F;且OE平分∠BOI,OH平分∠AOE.
(1)试说明:OH//FE;
(2)若∠FED=70°,试求∠BOF和∠HOI的度数.
26. (本小题8.0分)
卡塔尔世界杯期间,某商店特购进世界杯吉祥物“拉伊卜”摆件和挂件共90个进行销售.已知“拉伊卜”摆件的进价为40元/个,“拉伊卜”挂件的进价为25元/个.
(1)若购进“拉伊卜”摆件和挂件共花费了2850元,请分别求出购进“拉伊卜”摆件和挂件的数量;
(2)该商店计划将“拉伊卜”摆件售价定为50元/个,“拉伊卜”挂件售价定为30元/个,若购进的90个“拉伊卜”摆件和挂件全部售完,且至少盈利725元,求购进的“拉伊卜”挂件不能超过多少个?
答案和解析
1.【答案】C
【解析】解:在3.14,−17, 5,0这四个数中,属于无理数的是 5.
故选:C.
根据无理数的定义判断即可.
本题考查了无理数,掌握无限不循环小数是无理数是解题的关键.
2.【答案】C
【解析】解:根据对顶角的概念可知,
A、B、D中的∠1与∠2都不符合对顶角的特征,
而C图中的∠1与∠2只有一个公共顶点且两个角的两边互为反向延长线,属于对顶角.
故选C.
对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.根据此定义进行判断即可.
本题主要考查了对顶角的概念,解题时要紧扣概念中的关键词语,如:两条直线相交,有一个公共顶点,反向延长线等.
3.【答案】D
【解析】解:因为xy=0,所以x、y中至少有一个是0;
当x=0时,点在y轴上;
当y=0时,点在x轴上.
当x=0,y=0时是坐标原点.
所以点P的位置是在x轴上或在y轴上.
故选:D.
根据坐标轴上的点的坐标特点解答即可.
本题主要考查了坐标轴上点的坐标特点,即点在x轴上点的坐标为纵坐标等于0;点在y轴上点的坐标为横坐标等于0.
4.【答案】A
【解析】解:将①代入②得,x+4x=6.
故选:A.
直接把①代入②即可.
本题考查的是解二元一次方程组,熟知解二元一次方程组的代入消元法是解题的关键.
5.【答案】D
【解析】解:由不等式x>ax>3的解集是x>a,
根据大大取大,a≥3.
选:D.
根据x的取值来分析a的取值.
本题考查不等式解集的表示方法,注意这里的a可以等于3的.
6.【答案】C
【解析】解:不少于25次的人数为:12+5=17(人),
故选:C.
由图可知,25~30为12人,30~35为5人,则不少于25次即为两部分的和.
本题主要考查了从频数分布直方图中提取信息的能力,提取出所需要的信息是解题的关键.
7.【答案】A
【解析】解:将不等式组x>2x≥3的解集表示在数轴上,正确的是:
故选:A.
首先解两个不等式,本题可根据数轴的性质“实心圆点包括该点用“≥”,“≤”表示,空心圆圈不包括该点用“<”,“>”表示,大于向右小于向左.”画出数轴.
本题考查不等式组解集的表示方法.把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
8.【答案】D
【解析】解:点P(−3,−5)关于x轴对称的点的坐标是(−3,5).
故选:D.
点关于x轴对称的点的坐标的特点是横坐标不变,纵坐标变为相反数,由此即可求解.
本题主要考查点的对称性,掌握平面直角坐标系中点的对称性知识是解题的关键.
9.【答案】A
【解析】解:如图,
由题意得:∠E=90°,AB//CD,
∴∠3=∠1=125°,
∵∠3是△ABE的外角,
∴∠2=∠3−∠E=35°,
故选:A.
由平行线的性质可得∠3=∠1=125°,再利用三角形的外角性质即可求解.
本题主要考查平行线的性质,熟记平行线的性质是解题的关键.
10.【答案】A
【解析】解:依题意得:3x=5y2y−x=1,
故选:A.
设每块小长方形地砖的长为x cm,宽为y cm,利用长方形的对边相等及图②中的阴影部分(正方形)的面积为1(边长为1),即可得出关于x,y的二元一次方程组.
本题考查了由实际问题抽象出二元一次方程组,找准等量关系是解题的关键.
11.【答案】D
【解析】解:方程组3a1x+2b1y=5c13a2x+2b2y=5c2可以变形为:方程组a1⋅35x+b1⋅25y=c1a2⋅35x+b2⋅25y=c2,
设35x=m,25y=n,则方程组可变为a1m+b1n=c1a2m+b2n=c2,
∴m=3,n=4,
即35x=3,25y=4,
解得x=5y=10.
故选:D.
用换元法求解方程组的解.
此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.弄清题意是解本题的关键.
12.【答案】A
【解析】解:观察发现,每6个点形成一个循环,
∵A6(6,0),
∴OA6=6,
∵2022÷6=337,
∴点A2022的位于第337个循环组的第6个,
∴点A2022的横坐标为6×337=2022,其纵坐标为:0,
∴点A2022的坐标为(2022,0).
故选:A.
观察发现,每6个点形成一个循环,再根据点A6的坐标及2022÷6所得的整数及余数,可计算出点A2022的横坐标,再根据余数对比第一组的相应位置的数可得其纵坐标.
本题考查了平面直角坐标系中的点的规律问题,发现题中的规律并正确计算出点A2022所处的循环组是解题的关键.
13.【答案】14
【解析】解:∵正数有两个平方根,他们互为相反数,
∴m+(−3m+1)=0,解得:m=12,
∴a=(12)2=14,
故答案为:14.
根据平方根的定义即可求解.
本题主要考查了平方根,掌握平方根的定义是解题的关键.
14.【答案】6
【解析】解:∵最大值为35,最小值为14,
∴在样本数据中最大值与最小值的差为35−14=21,
又∵组距为4,
∴应该分的组数=21÷4=5.25,
∴应该分成6组.
故答案为:6.
根据最大值为35,最小值为14,求出最大值与最小值的差,再根据组距为4,组数=(最大值−最小值)÷组距计算即可.
本题考查了组距与组数,属于基础题,用到的知识点是组数=(最大值−最小值)÷组距,注意要进位.
15.【答案】<
【解析】解:∵4<5<9,
∴2< 5<3<π,
则 5<π,
故答案为:<.
估算出 5在哪两个连续整数之间即可求得答案.
本题考查无理数的估算及实数的大小比较,估算出 5在哪两个连续整数之间是解题的关键.
16.【答案】50
【解析】解:如图,当∠1+∠2=180°,即∠2=180°−∠1=180°−130°=50°时,a//b.
故答案为:50.
根据“同旁内角互补,两直线平行”进行填空.
本题考查了平行线的判定.解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养学生“执果索因”的思维方式与能力.
17.【答案】(2,−1)
【解析】解:因为A(−2,1)和B(−2,−3),
所以可得点C的坐标为(2,−1),
故答案为:(2,−1).
根据A(−2,1)和B(−2,−3)的坐标以及与C的关系进行解答即可.
此题考查坐标问题,关键是根据A(−2,1)和B(−2,−3)的坐标以及与C的关系解答.
18.【答案】−6≤x<−4
【解析】解:由题意知−3≤x2<−2,
解得−6≤x<−4,
故答案为:−6≤x<−4.
根据题意得出不等式组,再求出不等式组的解集即可.
本题考查了有理数的大小比较和解一元一次不等式组,能求出不等式组的解集是解此题的关键.
19.【答案】解:根据题意得:c>0,a−b>0,a+b<0,b−c<0,
则原式=c−a+b+a+b+c−b
=2c+b.
【解析】根据数轴上点的位置判断出绝对值里边式子的符号,利用绝对值的代数意义化简,去括号合并即可得到结果.
此题考查了实数的运算,以及实数与数轴,判断出绝对值里边式子的正负是解本题的关键.
20.【答案】解:(1)x−y=4①2x+y=5②,
①+②得:3x=9,
解得:x=3,
把x=3代入①得:3−y=4,
解得:y=−1,
∴原方程组的解为:x=3y=−1;
(2)2x−3y=3①x+2y=−2②,
②×2得:2x+4y=−4③,
③−①得:7y=−7,
解得:y=−1,
把y=−1代入②得:x−2=−2,
解得:x=0,
∴原方程组的解为:x=0y=−1.
【解析】(1)利用加减消元法进行计算,即可解答;
(2)利用加减消元法进行计算,即可解答.
本题考查了解二元一次方程组,熟练掌握加减消元法是解题的关键.
21.【答案】解:由2x−1<7,得:x<4,
由3x−12≥x+1,得:x≥3,
则不等式组的解集为3≤x<4,
将解集表示在数轴上如下:
【解析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
22.【答案】解:∵AB//CD,
∴∠BPQ=∠CQP,
∵∠1=∠2,
∴∠BPQ−∠1=∠CQP−∠2,
∴∠EPQ=∠FQP,
∴EP//FQ,
∴∠E=∠F.
【解析】先根据平行线的性质可得∠BPQ=∠CQP,从而利用等式的性质可得∠EPQ=∠FQP,然后利用内错角相等,两直线平行可得EP//FQ,从而利用平行线的性质可得∠E=∠F,即可解答.
本题考查了平行线的判定与性质,根据题目的已知条件并结合图形进行分析是解题的关键.
23.【答案】2 9 (m+3,n+2)
【解析】解:(1)b=2,c=9;
故答案为:2,9;
(2)如图,△A1B1C1为所作;
(3)P(m,n)平移后的对应点P1的坐标为(m+3,n+2).
故答案为:(m+3,n+2).
(1)利用A点和A1点的坐标特征得到△ABC先向右平移3个单位,再向上平移2个单位得到△A1B1C1,从而得到c、b的值;
(2)根据A1、B1、C1点的坐标描点即可;
(3)根据(1)中点的平移规律求解.
本题考查了作图−平移变换:作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
24.【答案】30 20% 90
【解析】解:(1)∵被调查的总人数为10÷10%=100(名),
∴m=100×30%=30,n=1−(10%+15%+25%+30%)=20%,
补全图形如下:
故答案为:30、25%;
(2)扇形统计图中“C组”所对应的圆心角的度数是360°×20%=72°,
故答案为:72°;
(3)964×(10%+15%+25%)=482(名),
答:估计这所学校本次比赛听写不合格的学生人数有482名.
(1)根据A组频数及其所占百分比求得总人数,总人数乘以D组百分比可得m,根据百分比之和为1可得n的值;
(2)用360°乘以E组百分比可得;
(3)总人数乘以样本中A、B组百分比之和可得.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
25.【答案】解:(1)因为EF平分∠OED,
所以∠OEF=∠FED=12∠OED,
因为OH平分∠AOE,
所以∠HOE=12∠AOE,
因为AB//CD,
所以∠OED=∠AOE,
所以∠OEF=∠HOE,
所以OH//FE;
(2)因为∠FED=70°,
所以∠OED=2∠FED=140°,
因为∠OEH+∠OED=180°,
所以∠OEH=180°−140°=40°,
因为AB//CD,
所以∠BOE=∠OEH=40°,
因为OF⊥OE,
所以∠EOF=90°,
所以∠BOF=90°−40°=50°;
因为OE平分∠BOI,
所以∠IOE=∠BOE=40°,
因为OH//FE,
所以∠HOE=∠OEF=∠FED=70°,
所以∠HOI=∠HOE−∠IOE=70°−40°=30°.
【解析】(1)由角平分线的定义可得∠OEF=12∠OED,∠HOE=12∠AOE,结合平行线的性质可得∠OEF=∠HOE,进而可证明结论;
(2)由平角的定义可求解∠OEH的度数,利用平行线的性质可得∠BOE=40°,结合垂直的定义可求解∠BOF的度数;根据角平分线的定义可求解∠IOE的度数,进而可求解∠HOI的度数.
本题主要考查平行线的性质与判定,角平分线的定义,掌握平行线的性质与判定是解题的关键.
26.【答案】解:(1)设购进“拉伊卜”摆件x个,“拉伊卜”挂件y个,
依题意得:x+y=9040x+25y=2850,
解得:x=40y=50,
答:购进“拉伊卜”摆件40个,“拉伊卜”挂件50个.
(2)设购进“拉伊卜”挂件m个,则购进“拉伊卜”摆件(90−m)个,
佽题意得:(30−25)m+(50−40)(90−m)≥725,
解得:m≤35.
答:购进的“拉伊卜”挂件不能超过35个.
【解析】(1)设购进“拉伊卜”摆件x个,“拉伊卜”挂件y个,根据题意列方程组解题即可;
(2)设购进“拉伊卜”挂件m个,利用不等式解题即可.
本题考查二元一次方程组的应用和一元一次不等式的应用,能找到等量关系列出方程或不等式是解题的关键.
2022-2023学年山东省济宁市梁山县八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年山东省济宁市梁山县八年级(下)期末数学试卷(含解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山东省济宁市梁山县八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年山东省济宁市梁山县八年级(下)期末数学试卷(含解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山东省济宁市梁山县八年级(下)期中数学试卷(含解析): 这是一份2022-2023学年山东省济宁市梁山县八年级(下)期中数学试卷(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












