数学2.2.1平方差公式优质课教学设计及反思

2.2  乘法公式

2.2.1  平方差公式

【知识与技能】

1.使学生理解和掌握平方差公式.

2.会利用公式进行计算，能够掌握平方差公式的一些应用.

【过程与方法】

经历探索平方差公式的过程，增强了数和符号的意识，培养学生发现问题、提出问题的能力.

【情感态度】

在探索和交流的过程中，培养学生与人协作的习惯，质疑的精神.

【教学重点】

弄清平方差公式的来源及其结构特点，能用自己的语言说明公式及其特点.

【教学难点】

准确理解和掌握公式的结构特征.

一、情景导入，初步认知

回顾整式乘法中多项式与多项式相乘

1.多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.符号表示：(m+b)(n+a)=mn+ma+bn+ba.

2.两项式乘以两项式，结果可能是两项吗？请你举例说明.

【教学说明】平方差公式是多项式乘法运算中一个重要的公式，它的得出可以直接利用多项式乘以多项式法则，设计这一环节的目的是在复习上节课知识的基础上，为本节课的学习做好知识准备.

二、思考探究，获取新知

1.计算下列各式：

(1)(a+1)(a-1);

=a2-a+a-12

=a2-1

(2)(a+2)(a-2);

=a+-2a+2a-22

=a＋-4

(3)(a+3)(a-3);=a2-3a+3a-32

=a2-9

(4)(a+4)(a-4).;

=a2-4a+4a-42

=a2-16

2.观察以上算式及其运算结果，你发现了什么规律？你能计算(a+b)(a-b)吗？【归纳结论】 平方差公式：(a+b)(a-b)＝a2-b2，两数和与两数差的积，等于它们的平方差.

【教学说明】在上一环节的基础上，引入形式特殊的多项式乘以多项式，使学生在计算过程中发现规律，体会规律的一般性，提出自己的猜想，并尝试用数学语言进行描述.

3.应用平方差公式时应注意些什么呢？

(1)注意平方差公式的适用范围;

(2)字母a、b可以是数，也可以是整式;

(3)注意计算过程中的符号和括号.

4.如图，将边长为a的大正方形减去一个边长为b的小正方形，并将剩余的部分沿虚线剪开，得到两个长方形，在将这两个长方形拼成如图2，你能用这两个图形来解释平方差公式吗？

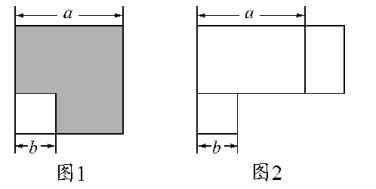
①请表示图1中阴影(紫色)部分的面积.

②小颖将阴影部分拼成了一个长方形(如图2)，这个长方形的长和宽分别是多少？你能表示出它的面积吗？

③比较①，②的结果，你能验证平方差公式吗?

④叙述平方差公式的数学表达式及文字表达式；

⑤试比较公式的两种表达式在应用上的差异.

【归纳结论】(a+b)(a-b)＝a2-b2

【教学说明】经过对两个图形的面积的计算，使学生明白可以通过几何图形对平方差公式进行验证.进一步加深对平方差公式的理解.

三、运用新知，深化理解

1.见教材P43例1、例2、例3.

2.填空题.

(x+6)(6-x)=,

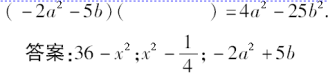
3.下列式中能用平方差公式计算的有(D)

①(x-y)(x+y)

②(3a-bc)(-bc-3a)

③(3-x+y)(3+x+y)

④(100+1)(100-1)

A.1个B.2个C.3个D.4个

4.下列式中,运算正确的是(C)

①(22a)2=4a2

②(－x+1)(1+x)=1－x2

③(m－1)2(1－m)3=(m－1)5

④2a×4b×8=2a+2b+3

A.①②  B.②③  C.②④  D.③④

5.乘法等式中的字母a、b表示(D)

A.只能是数

B.只能是单项式

C.只能是多项式

D.单项式、多项式都可以

6.计算：

(1)(2a-3b)(2a+3b)；

解：原式=(2a)2-(3b)2

=4a2-9b2

(2)(-p2+q)(-p2-q)；

解：原式=(-p2)2-(q)2

=p4-q2

(3)4a－7b4a+7b；

解：原式=(4a)2-(7b)2

=16a2-49b2

(4)－2m－n2m－n；

解：原式=-(-2m+n)(2n-(n)2)

=［(2m)2-n2］

=-(4m2-n2)

=n2-4m2

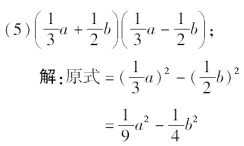
 (6)－［(5+2x)(5－2x)］;解：原式=-［(5+2x)(5-2x)］

=-［52-(2x)2］

=-25+4x2

(7)403×397.

解：原式=(400+3)(400-3)

=4002-32

=159991

7.计算(a+1)(a-1)(a2+1)(a4+1)(a8+1).

解：原式=(a2-1)(a2+1)(a4+1)(a8+1)

=(a4-1)(a4+1)(a8+1)

=(a8-1)(a8+1)

=a16-1

【教学说明】在深刻理解公式的基础上，借助例题训练学生正确应用公式计算，体会公式在简化运算中的作用，并通过巩固练习，进一步强化技能.

四、师生互动，课堂小结

1.平方差公式：(a+b)(a－b)=a2－b2公式的结构特点：左边是两个二项式的乘积，即两数和与这两数差的积；右边是两数的平方差.

2.应用平方差公式的注意事项：

(1)注意平方差公式的适用范围；

(2)字母a、b可以是数，也可以是整式；

(3)注意计算过程中的符号和括号.

1. 布置作业:教材第50页“习题2.

2”中第1题.2.完成同步练习册中本课时的练习.

本课让学生经历自主探索平方差公式的推导过程，采用自学为主的导学设计，在教学方法上采用以问题的形式，引导学生独立思考、探索，再通过讨论、交流，发现平方差公式的特点，教师适当的引导，使学生理解并掌握平方差公式的推导过程，通过练习巩固，力求突出重点、突破难点，使学生运用平方差公式解决问题的能力得到进一步提高.在整个教学过程中，分层次地培养学生数学思想和方法，养成良好的思维习惯.