人教版八年级数学下册 一次函数 检测题四（含答案）

这是一份人教版八年级数学下册 一次函数 检测题四（含答案），共6页。
第十九章一次函数一、选择题(每小题4分，共24分)1．下列函数中，是一次函数的有(　　)①y＝x；②y＝3x＋1；③y＝；④y＝kx－2.A．1个  B．2个  C．3个  D．4个2．已知函数y＝kx＋b，其中常数k＞0，b＜0，那么这个函数的图象不经过的象限是(　　)A．第一象限  B．第二象限    C．第三象限  D．第四象限3．对于函数y＝－2x＋1，下列结论正确的是(　　)A．它的图象必经过点(－1，2)B．它的图象经过第一、二、三象限C．当x＞1时，y＜0D．y的值随x值的增大而增大4．正比例函数y＝kx(k≠0)的图象过第二、四象限，则一次函数y＝x＋k的图象大致是(　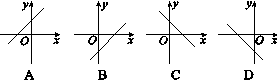　)5．点P(x，y)在第一象限内，且x＋y＝6，点A的坐标为(4，0)．设△OPA的面积为S，则下列图象中，能正确反映面积S与x之间的函数关系的图象是(　　)6．明君社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时间后，提高了工作效率．该绿化组完成的绿化面积S(单位：m2)与工作时间t(单位：h)之间的函数关系如图所示，则该绿化组提高工作效率前每小时完成的绿化面积是(　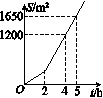　)A．300 m2  B．150 m2  C．330 m2  D．450 m2 二、填空题7．已知函数y＝(k－1)x＋k2－1.当k________时，它是一次函数；当k＝________时，它是正比例函数．8．在平面直角坐标系中，已知一次函数y＝2x＋1的图象经过P1(x1，y1)，P2(x2，y2)两点，若x1＜x2，则y1________y2(填“>”“<”或“＝”)．9．如图，一个正比例函数图象与一次函数y＝－x＋1的图象相交于点P，则这个正比例函数的解析式是________．10．若将直线y＝3x＋2沿y轴向下平移5个单位长度，则平移后直线与y轴的交点坐标为________．11．已知一次函数y＝kx＋b(k≠0)经过(2，－1)，(－3，4)两点，则其图象不经过第________象限．12．一辆汽车由A地开往B地，它距离B地的路程s(km)与行驶时间t(h)之间的关系如图所示，如果汽车一直快速行驶，那么可以提前________小时到达B地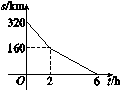．三、解答题(共46分)13．已知一次函数y＝mx－3m2＋12，请按要求解答问题：(1)m为何值时，函数图象过原点，且y随x的增大而减小？(2)若函数图象平行于直线y＝－x，求一次函数的解析式；(3)若点(0，－15)在函数图象上，求m的值．  
14.(6分)将长为30 cm、宽为10 cm的长方形白纸按图所示的方法黏合起来，黏合部分的宽为3 cm.设x张白纸黏合后的总长度为y cm，写出y与x之间的函数解析式(不要求写自变量的取值范围)，并求出当x＝20时y的值．         15．(10分)直线y＝2x－2与x轴交于点A，与y轴交于点B.(1)求点A，B的坐标；(2)点C在x轴上，且S△ABC＝3S△AOB，直接写出点C的坐标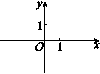．          16．(10分)小丽的家和学校在一条笔直的马路旁，某天小丽沿着这条马路去上学，她先从家步行到公交站台甲，再乘车到公交站台乙下车，最后步行到学校(在整个过程中小丽步行的速度不变)，图中的折线ABCDE表示小丽和学校之间的距离y(米)与她离家的时间x(分)之间的函数关系．(1)求小丽步行的速度及学校与公交站台乙之间的距离；(2)当8≤x≤15时，求y与x之间的函数解析式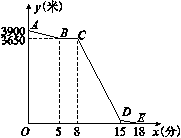．     17．(12分)已知两直线l1：y＝k1x＋b1，l2：y＝k2x＋b2，若l1⊥l2，则有k1·k2＝－1.(1)应用：已知直线y＝2x＋1与直线y＝kx－1垂直，求k的值；(2)已知直线经过点A(2，3)，且与直线y＝－x＋3垂直，求该直线所对应的函数解析式．          
详解详析1．B　[解析] ①②属于一次函数；③自变量x在分母上，故不是一次函数；④当k＝0时，就不是一次函数，故一共有2个一次函数．2．B　[解析] ∵函数y＝kx＋b中k＞0，b＜0，∴函数图象经过第一、三、四象限，不经过第二象限．3．C　[解析] A项，令y＝－2x＋1中的x＝－1，则y＝3，∴一次函数的图象不过点(－1，2)，即A项不正确；B项，∵k＝－2＜0，b＝1＞0，∴一次函数的图象经过第一、二、四象限，即B项不正确；C项，∵k＝－2＜0，∴一次函数中的y随x的增大而减小．∵令y＝－2x＋1中的x＝1，则y＝－1，∴当x＞1时，y＜0成立，即C项正确；D．∵k＝－2＜0，∴一次函数中y随x的增大而减小，即D项不正确．故选C.4．B　[解析] 因为正比例函数y＝kx的图象过第二、四象限，所以k＜0，因此一次函数y＝x＋k中y随x的增大而增大，且其图象与y轴负半轴相交，即函数图象位于第一、三、四象限．故选B.5．C　[解析] ∵点P(x，y)在第一象限内，且x＋y＝6，∴y＝6－x(0＜x＜6，0＜y＜6)．∵点A的坐标为(4，0)，∴S＝×4×(6－x)＝12－2x(0＜x＜6)，∴C符合．6．B　[解析] 如图，设直线AB的解析式为y＝kx＋b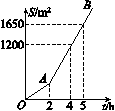，故直线AB的解析式为y＝450x－600，当x＝2时，y＝450×2－600＝300，300÷2＝150(m2)．即该绿化组提高工作效率前每小时完成的绿化面积是150 m2.7．≠1　－18．<　[解析] 一次函数y＝2x＋1中y随x的增大而增大，所以若x1＜x2，则y1＜y2.9．y＝－2x　[解析] ∵正比例函数图象与一次函数y＝－x＋1的图象相交于点P，点P的纵坐标为2，∴2＝－x＋1，解得x＝－1，∴点P的坐标为(－1，2)，∴设正比例函数的解析式为y＝kx，∴2＝－k，解得k＝－2，∴正比例函数的解析式为y＝－2x.10．(0，－3)　[解析] 将直线y＝3x＋2沿y轴向下平移5个单位长度可得y＝3x＋2－5，即y＝3x－3，∴平移后直线与y轴的交点坐标为(0，－3)．11．三12．2　[解析] 320－160＝160(千米)，160÷2＝80(千米/时)，320÷80＝4(时)，6－4＝2(时)．13．解：(1)∵一次函数y＝mx－3m2＋12，函数图象过原点，且y随x的增大而减小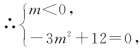，解得m＝－2，即当m＝－2时，函数图象过原点，且y随x的增大而减小．(2)∵一次函数y＝mx－3m2＋12，函数图象平行于直线y＝－x，∴m＝－1，∴－3m2＋12＝－3×(－1)2＋12＝9，∴一次函数的解析式是y＝－x＋9.(3)∵一次函数y＝mx－3m2＋12，点(0，－15)在该函数图象上，∴m×0－3m2＋12＝－15，解得m＝±3，即m的值是±3.14．解：由题意，得y＝27x＋3.当x＝20时，y＝27×20＋3＝543.15．解：(1)令y＝2x－2中y＝0，则2x－2＝0，解得x＝1，∴A(1，0)．令y＝2x－2中x＝0，则y＝－2，∴B(0，－2)．(2)根据题意画出图形，如图所示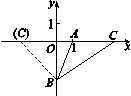．设点C的坐标为(m，0)，∵S△ABC＝3S△AOB，∴|m－1|＝3，解得m＝4或m＝－2，即点C的坐标为(4，0)或(－2，0)．16．解：(1)(3900－3650)÷5＝250÷5＝50(米/分)，即小丽步行的速度为50米/分．(18－15)×50＝150(米)．即学校与公交站台乙之间的距离为150米．(2)设过C，D两点的直线的函数解析式为y＝kx＋b.∵C(8，3650)，D(15，150)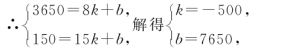，∴当8≤x≤15时，y＝－500x＋7650.17．解：(1)∵直线y＝2x＋1与直线y＝kx－1垂直，∴2k＝－1，解得k＝－.(2)∵过点A的直线与直线y＝－x＋3垂直，∴可设过点A的直线所对应的函数解析式为y＝3x＋b.把点A的坐标(2，3)代入，得3＝3×2＋b，解得b＝－3，∴该直线所对应的函数解析式为y＝3x－3.