高中数学人教A版 (2019)必修 第二册8.3 简单几何体的表面积与体积复习练习题

8.3 简单几何体的表面积与体积 8.3.1 棱柱、棱锥、棱台的表面积和体积

A级　基础巩固

1.若某长方体同一顶点上的三条棱长分别为1,2,3,则该长方体的表面积为 (　　)

A.22 B.20 C.10 D.11

解析:所求长方体的表面积S=2×(1×2)+2×(1×3)+2×(2×3)=22.

答案:A

2.如图所示,正方体ABCD-A1B1C1D1的棱长为1,则三棱锥D1-ACD的体积是 (　　)

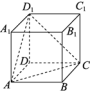
A. B.C. D.1

解析:三棱锥D1-ACD的体积V=S△ACD×D1D=××1×1×1=.

答案:A

3.(2022·全国甲卷,理)如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为 (　　)

A.8 B.12 C.16 D.20

解析:三视图对应的几何体是放倒的直四棱柱,如图,直四棱柱的高为2,底面是上底为2,下底为4,高为2的梯形,所以体积V=Sh=×(2+4)×2×2=12.故选B.

答案:B

4.(2022·新高考全国Ⅰ卷)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m时,相应水面的面积为140.0 km2;水位为海拔157.5 m时,相应水面的面积为180.0 km2.将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔 148.5 m上升到157.5 m时,增加的水量约为(≈2.65) (　　)

A.1.0×109 m3 B.1.2×109 m3

C.1.4×109 m3 D.1.6×109 m3

解析:由已知得该棱台的高为157.5-148.5=9(m),所以该棱台的体积V=×9×(140++180)×106=60×(16+3)×106≈

60×(16+3×2.65)×106=1.437×109≈1.4×109(m3).故选C.

答案:C

5.如图所示,某几何体的下半部分为正方体ABCD-A'B'C'D',上半部分为正四棱锥S-ABCD,若几何体的高为5,棱AB=2,则该几何体的体积为　　　　. 

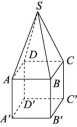
解析:V正方体=23=8,V四棱锥S-ABCD=×22×(5-2)=4.所以该几何体的体积V=V正方体+V四棱锥S-ABCD=12.

答案:12

6.在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余部分的体积之比.

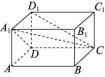
解:已知长方体可以看成直四棱柱,设它的底面ADD1A1的面积为S,高为h,则它的体积为V=Sh.

而棱锥C-A1DD1的底面积为S,高为h,

故=×Sh=Sh,

余下部分的体积为Sh-Sh=Sh.

所以棱锥C-A1DD1的体积与剩余部分的体积之比为1∶5.

B级　能力提升

7.(2021·新高考全国Ⅱ卷)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为 (　　)

A.20+12 B.28C. D.

答案:D

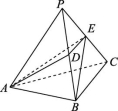
8.在三棱锥P-ABC中,D,E分别为PB,PC的中点,记三棱锥D-ABE的体积为V1,三棱锥P-ABC的体积为V2,则=　　　　. 

解析:如图所示,设点C到平面PAB的距离为h,三角形PAB的面积为S,则V2=Sh,V1=V棱锥E-ADB=×S×h=Sh,所以=.

答案:

9.有位油漆工用一把长度为50 cm,横截面半径为10 cm的圆柱形刷子给一块面积为 10 m2的木板涂油漆,且圆柱形刷子以每秒5周的速度在木板上匀速滚动前进,则油漆工完成任务所需的时间是多少?(精确到0.01 s)

解:由题意可知,圆柱形刷子滚动一周涂过的面积就等于圆柱的侧面积,50 cm=0.5 m,10 cm=0.1 m.

因为圆柱的侧面积为S侧=2π×0.1×0.5=0.1π (m2),且圆柱形刷子以每秒5周的速度匀速滚动,

所以圆柱形刷子每秒滚过的面积为0.5π m2.

所以油漆工完成任务所需的时间t==≈6.37(s).

C级　挑战创新

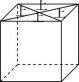
10.开放性问题现有一个棱长为1的正方体礼品盒,需要买一张正方形彩纸将其完全包住,请你设计一个方案,在不将彩纸撕开的情况下,所买彩纸费用最少(注:彩纸按面积收费).

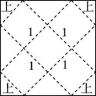
解:如图①为棱长为1的正方体礼品盒,先把正方体的表面按如图所示的方式展成平面图形,再把平面图形尽可能拼成面积较小的正方形,如图②所示,由图知正方形的边长为2,其面积为8.

即买边长为2的正方形彩纸所需费用最少.

①

②