人教版八年级上册13.3.1 等腰三角形巩固练习

这是一份人教版八年级上册13.3.1 等腰三角形巩固练习，共10页。
人教版2021年八年级数学上册课时作业本
轴对称与等腰三角形-等腰三角形解答题专练
如图,△ABC中，AB=AC=5，AB的垂直平分线DE交AB、AC于E、D，
(1）若△BCD的周长为8，求BC的长；
(2）若∠ABD：∠DBC=1：1，求∠A的度数．








如图，在△ABC中，已知点D在线段AB的反向延长线上，过AC的中点F作线段GE交∠DAC的平分线于E，交BC于G，且AE∥BC.
(1)求证：△ABC是等腰三角形；
(2)若AE=8cm，AB=10cm，GC=2BGcm，求△ABC的周长．
















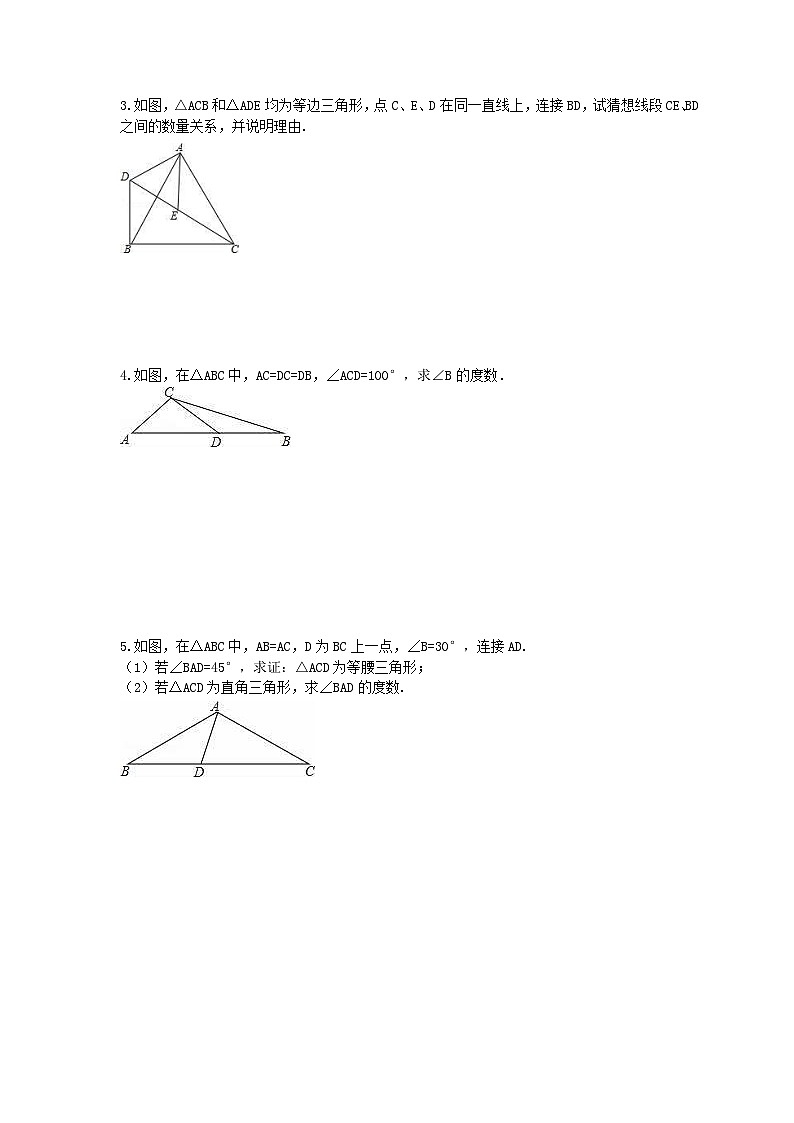
如图，△ACB和△ADE均为等边三角形，点C、E、D在同一直线上，连接BD，试猜想线段CE、BD之间的数量关系，并说明理由.






如图，在△ABC中，AC=DC=DB，∠ACD=100°，求∠B的度数．










如图，在△ABC中，AB=AC，D为BC上一点，∠B=30°，连接AD.
（1）若∠BAD=45°，求证：△ACD为等腰三角形；
（2）若△ACD为直角三角形，求∠BAD的度数.













如图，在△ABC中，已知点D在线段AB的反向延长线上，过AC的中点F作线段GE交∠DAC的平分线于E，交BC于G，且AE∥BC.
(1)求证：△ABC是等腰三角形；
(2)若AE=8，AB=10，GC=2BG，求△ABC的周长.








如图，已知△ABC中，AB=AC，∠BAC=90°，分别过B、C向过点A的直线作垂线，垂足分别为点E、F．
（1）如图（1），过A的直线与斜边BC不相交时，求证：①△ABE≌△CAF； ②EF=BE+CF
（2）如图（2），过A的直线与斜边BC相交时，其他条件不变，若BE=10，CF=3，试求EF的长．



















如图：AD为△ABC的高，∠B=2∠C，用轴对称图形说明：CD=AB+BD．






如图,已知ΔABC中,∠ACB=90°,CD⊥AB于D,BF平分∠ABC交CD于E,交AC于F.
求证：CE=CF．








已知，如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=50°
（1）求证：①AC=BD；②∠APB=50°；
（2）如图②，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系为 ，∠APB的大小为








如图，在△ABC中，∠C=90°，AC=BC，∠BAC的平分线AE交BC于点D，且AE⊥BE.
(1)求∠DBE的大小；
(2)求证：AD=2BE.








如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF．
（1）求证：BG=CF；
（2）请你判断BE+CF与EF的大小关系，并说明理由．


　


在△ABC中，AB=AC．
（1）如图1，如果∠BAD=30°，AD是BC上的高，AD=AE，则∠EDC=
（2）如图2，如果∠BAD=40°，AD是BC上的高，AD=AE，则∠EDC=
（3）思考：通过以上两题，你发现∠BAD与∠EDC之间有什么关系？请用式子表示：
（4）如图3，如果AD不是BC上的高，AD=AE，是否仍有上述关系？如有，请你写出来，并说明理由．




如图，已知△ABC中，AB=AC=12cm，BC=9cm，点D为AB的中点.
（1）如果点P在线段BC上以3cm/s的速度由点B向点C运动，同时点Q在线段CA上由点C向点A运动.
①若点P的运动速度与点Q的运动速度相等，1秒钟时，△BPD与△CQP是否全等，请说明理由？
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
（2）若点Q以（1）②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC的三边运动，直接写出经过多长时间点P与点Q第一次相遇.










参考答案
①3，②36°
（1）证明略；(2)32cm；


解：CE=BD，
理由：∵△ACB和△ADE均为等边三角形，∴AD=AE，AB=AC，∠DAE=∠BAC=60°，
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE，∴∠DAB=∠EAC.
在△ADB和△AEC中，，∴△ADB≌△AEC（SAS），∴CE=BD.

解：∵AC=DC=DB，∠ACD=100°，
∴∠CAD=（180°﹣100°）÷2=40°，
∵∠CDB是△ACD的外角，
∴∠CDB=∠A+∠ACD=100°=40°+100°=140°，
∵DC=DB，
∴∠B=（180°﹣140°）÷2=20°．

解：
（1）证明：∵AB=AC，∠B=30°，∴∠B=∠C=30°，
∴∠BAC=180°﹣30°﹣30°=120°，
∵∠BAD=45°，
∴∠CAD=∠BAC﹣∠BAD=120°﹣45°=75°，∠ADC=∠B+∠BAD=75°，
∴∠ADC=∠CAD，∴AC=CD，即△ACD为等腰三角形；
（2）解：有两种情况：
①当∠ADC=90°时，
∵∠B=30°，
∴∠BAD=∠ADC﹣∠B=90°﹣30°=60°；
②当∠CAD=90°时，
∠BAD=∠BAC﹣∠CAD=120°﹣90°=30°；
即∠BAD的度数是60°或30°.




（1）证明：
①∵BE⊥EF，CF⊥EF，∴∠AEB=∠CFA=90°，
∴∠EAB+∠EBA=90°，
∵∠BAC=90°，
∴∠EAB+∠FAC=90°，
∴∠EBA=∠FAC，
在△AEB与△CFA中
∴△ABE≌△CAF（AAS），
②∵△ABE≌△CAF，
∴EA=FC，EB=FA，
∴EF=AF+AE=BE+CF；
（2）解：∵BE⊥AF，CF⊥AF
∴∠AEB=∠CFA=90°
∴∠EAB+∠EBA=90°
∵∠BAC=90°
∴∠EAB+∠FAC=90°
∴∠EBA=∠FAC，
在△AEB与△CFA中
∴△ABE≌△CAF（AAS），
∴EA=FC，EB=FA，
∴EF=FA﹣EA=EB﹣FC=10﹣3=7．

证明：在CD上取一点E使DE=BD，连接AE．

∵BD=DE，且∠AED为△AEC的外角，∠B=2∠C，
∴∠B=∠AED=∠C+∠EAC=2∠C，
∴∠EAC=∠C，∴AE=EC；则CD=DE+EC=AB+BD．

证明：
∵∠ACB＝90°,CD⊥AB∴∠CBF＋∠CFB＝∠DBE＋∠DEB＝90°
∵BF平分∠ABC∴∠CBF＝∠DBE
∵∠CBF＋∠CFB＝∠DBE＋∠DEB∴∠CFB＝∠DEB
∵∠FEC＝∠DEB∴∠CFB＝∠FEC∴CE＝CF

证明：（1）∵∠AOB=∠COD=50°，∴∠AOC=∠BOD，
在△AOC和△BOD中，∴△AOC≌△BOD，∴AC=BD，∠CAO=∠DBO，
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB，∴∠APB=∠AOB=50°．
（2）解：AC=BD，∠APB=α，理由是：）∵∠AOB=∠COD=50°，∴∠AOC=∠BOD，
在△AOC和△BOD中，∴△AOC≌△BOD，∴AC=BD，∠CAO=∠DBO，
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB，∴∠APB=∠AOB=α，
故答案为：AC=BD，α．

解：(1)∵∠C=90°，AC=BC，
∴∠BAC=45°，
∵AE是∠BAC的平分线，
∴∠CAD=∠BAC=22.5°，
∵AE⊥BE，∴∠BED=90°，
∴∠ACD=∠BED=90°，
∵∠ADC=∠BDE，
∴∠DBE=∠CAD=22.5°.
(2)延长AC、BE交于点G.

∵AE⊥BG，∴∠AEB=∠AEG=90°，
在△AEB和△AEG中，，
∴△AEB≌△AEG，
∴BE=EG，
在△ACD和△BCG中，，
∴△ACD≌△BCG，
∴AD=BG=2BE，
∴AD=2BE.

解：（1）∵BG∥AC，∴∠DBG=∠DCF．∵D为BC的中点，∴BD=CD
又∵∠BDG=∠CDF，在△BGD与△CFD中，∵
∴△BGD≌△CFD（ASA）．∴BG=CF．
（2）BE+CF＞EF．∵△BGD≌△CFD，∴GD=FD，BG=CF．
又∵DE⊥FG，∴EG=EF（垂直平分线到线段端点的距离相等）．
∴在△EBG中，BE+BG＞EG，即BE+CF＞EF．
　
解：（1）∵在△ABC中，AB=AC，AD是BC上的高，
∴∠BAD=∠CAD，∵∠BAD=30°，∴∠BAD=∠CAD=30°，
∵AD=AE，∴∠ADE=∠AED=75°，∴∠EDC=15°．
（2）∵在△ABC中，AB=AC，AD是BC上的高，∴∠BAD=∠CAD，
∵∠BAD=40°，∴∠BAD=∠CAD=40°，
∵AD=AE，∴∠ADE=∠AED=70°，∴∠EDC=20°．
（3）∠BAD=2∠EDC（或∠EDC=0.5∠BAD）
（4）仍成立，理由如下
∵AD=AE，∴∠ADE=∠AED，
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=（∠EDC+∠C）+∠EDC=2∠EDC+∠C
又∵AB=AC，∴∠B=∠C∴∠BAD=2∠EDC．
故分别填15°，20°，∠EDC=0.5∠BAD

答案为：（1）全等；（2）全等；（3）24秒.