初中数学人教版九年级上册23.2.1 中心对称优质课ppt课件

这是一份初中数学人教版九年级上册23.2.1 中心对称优质课ppt课件，共23页。PPT课件主要包含了中心对称的性质，议一议，小试身手，灵活运用体会内涵，随堂练习，◆你还有疑问吗等内容，欢迎下载使用。

23.2.1中心对称和中心对称图形
（1）通过具体实例认识中心对称和中心对称图形，弄清楚中心对称和中心对称图形及其有关的概念.（2）探究并归纳出中心对称的性质.（3）会作与一个图形关于某个点成中心对称的另一个图形.
中心对称的概念和性质.
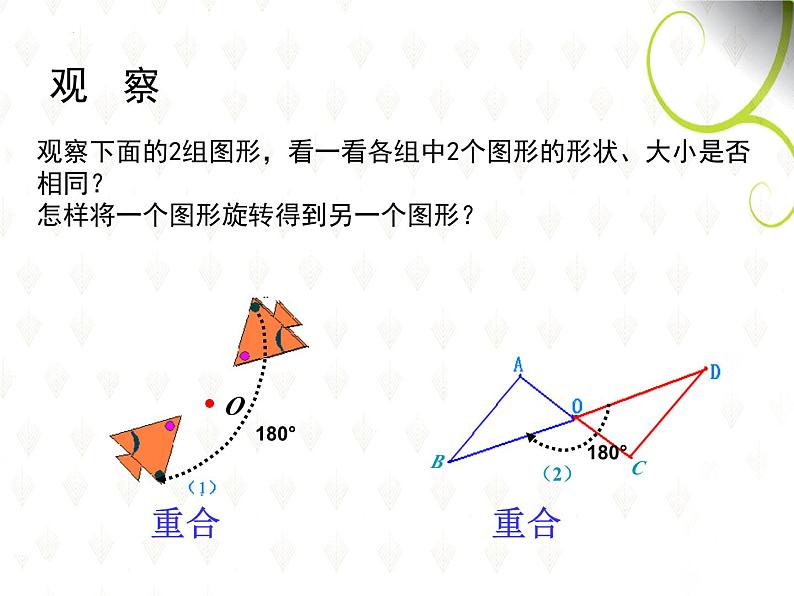
观察下面的2组图形，看一看各组中2个图形的形状、大小是否相同？怎样将一个图形旋转得到另一个图形？
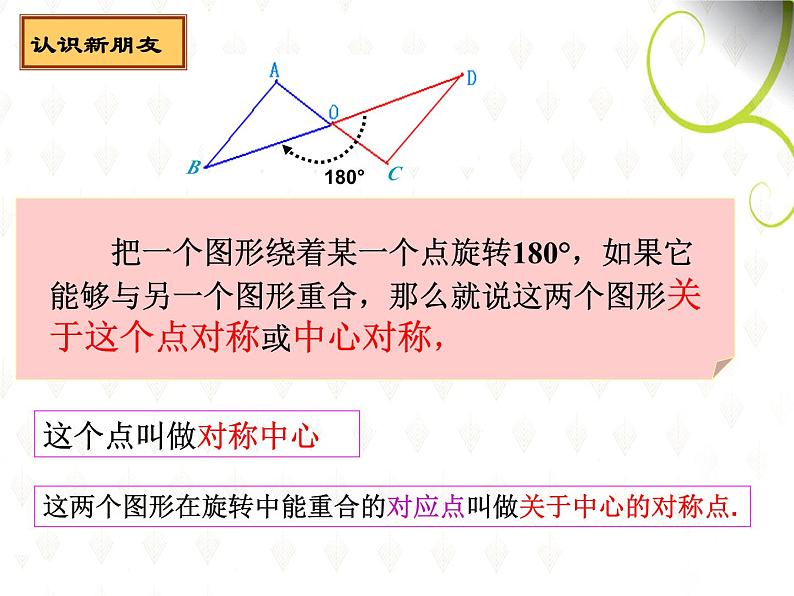
这两个图形在旋转中能重合的对应点叫做关于中心的对称点.
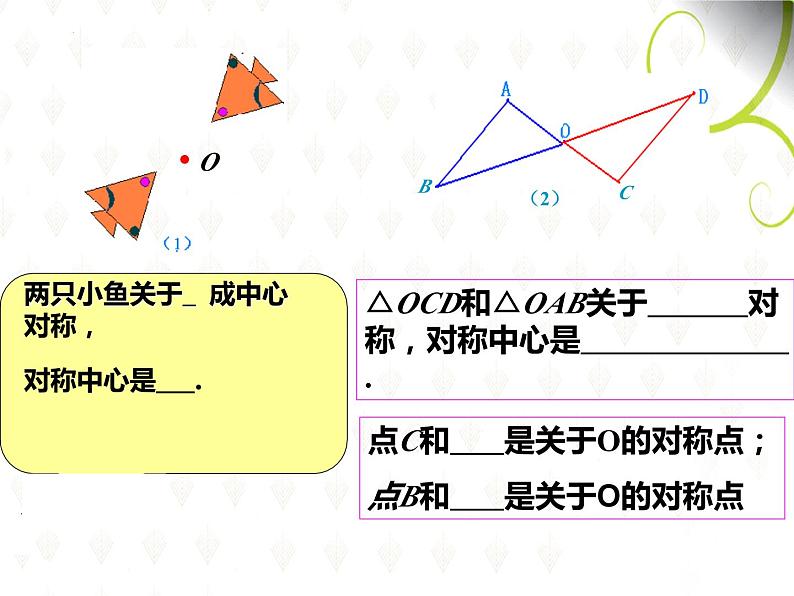
△OCD和△OAB关于 对称，对称中心是 .
点C和 是关于O的对称点；点B和 是关于O的对称点
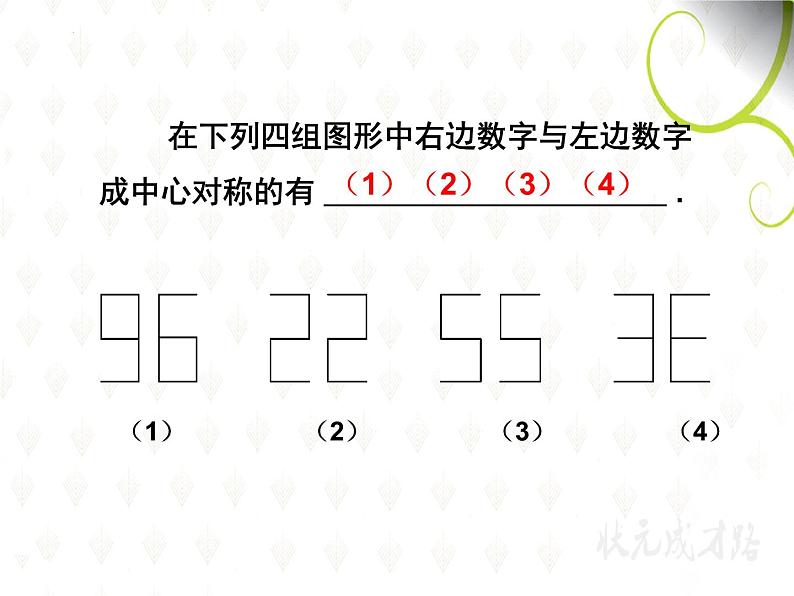
在下列四组图形中右边数字与左边数字成中心对称的有 .
（1） （2） （3） （4）
（1）（2）（3）（4）
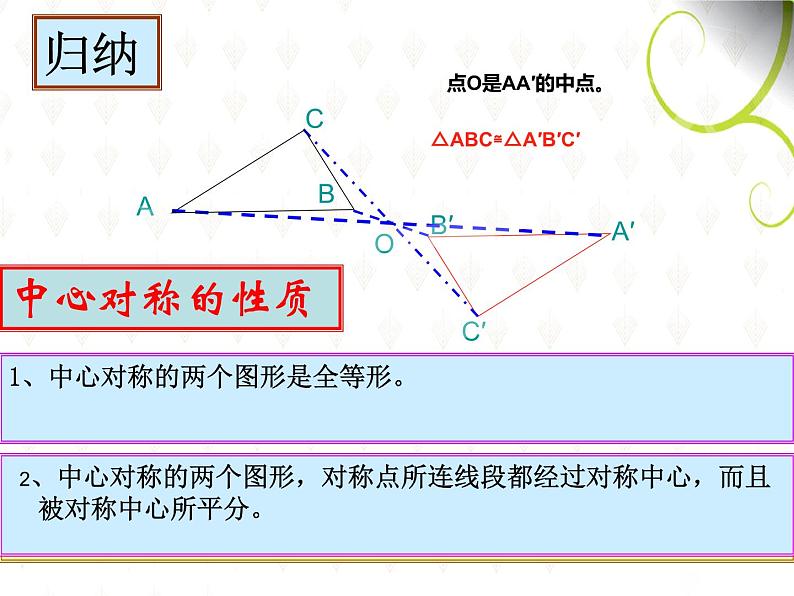
探究一：观察两个图形你发现了什么？
探究二：分别连接对称点AA′，BB′，CC′，你又发现 了什么？
点O是AA′的中点。
△ABC≌△A′B′C′
2、中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心所平分。
1、中心对称的两个图形是全等形。
中心对称与轴对称有什么区别?又有什么联系?
有一条对称轴---直线
有一个对称中心---点
图形沿对称轴对折(翻折180 °)后重合
图形绕对称中心旋转180°后重合
对称点的连线被对称轴垂直平分
对称点连线经过对称中心,且被对称中心平分
1、判断正误： （1）轴对称的两个图形一定是全等形，但全等的两个图形不一定是轴对称的图形。（ ） （2）成中心对称的两个图形一定是全等形。但全等的两个图形不一定是成中心对称的图形。 （ ） （3）全等的两个图形，不是成中心对称的图形，就是成轴对称的图形。 （ ）
2、选择题：如果两个图形成中心对称，下列说法正确的是 （ ）（1）对称点连线必经过对称中心，且被对称中心平分。（2）这两个图形一定是全等形。（3）把一个图形绕着对称中心旋转后定与另一个图形重合。（A）（1）（2）（3）（B）（2）（3）（C）（1）（3） （D）（1）（2）
（1）如果将线段AB绕它的中点O旋转180°，会出现什么情况？
线段AB绕它的中点O旋转180°后能与原来的图形重合.
（2）如果将平行四边形ABCD绕它的两条对角线的交点O旋转180°，又会出现什么情况？
平行四边形ABCD绕它的两条对角线的交点O旋转180°后能与原来的图形重合.
像这样，把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形.这个点就是它的对称中心.
下列标志中，可以看做是中心对称图形的是（ ）
1. 下列图形中，既是轴对称图形，又是中心对 称图形的是（ ） A．等边三角形 B．等腰三角形 C．平行四边形 D．正方形2. 下列图形中，是中心对称图形，但不一定是 轴对称图形的是（ ） A．正方形 B．矩形 C．菱形 D．平行四边形
中心对称与中心对称图形的区别与联系
比较中心对称和中心对称图形的概念，试说明它们有何区别与联系.
区别：中心对称是针对两个图形而言的，而中心对称图形是针对单个图形而言的. 联系：如果把成中心对称的两个图形看成一个整体，则该图形为中心对称图形；如果把一个中心对称图形相互对称的两部分看成两个图形，则它们成中心对称.
已知A点和O点，画出点A关于点O的对称点A'
已知线段AB和O点，画出线段AB关于点O 的对称线段A'B'
已知△ABC和O点，画出与 △ABC关于点O对称的△A′B′C′.
第二步：延长AO至A'，使OA'=OA，
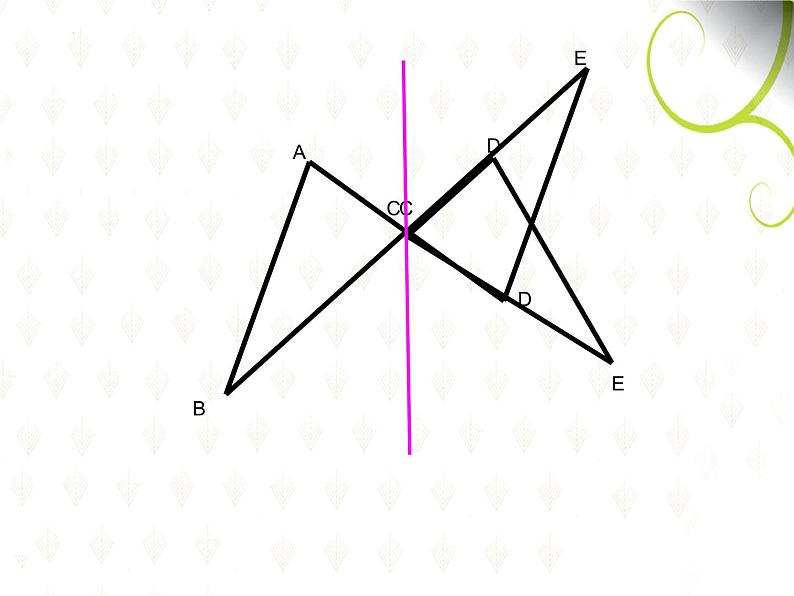
如图，D是△ABC的边AC上一点，画出△EFG，使它与△ ABC关于D成中心对称.
1.如图，已知△ABC与△A′B′C′中心对称，求出它们的对称中心O．
◆你在这堂课中获得哪些知识?