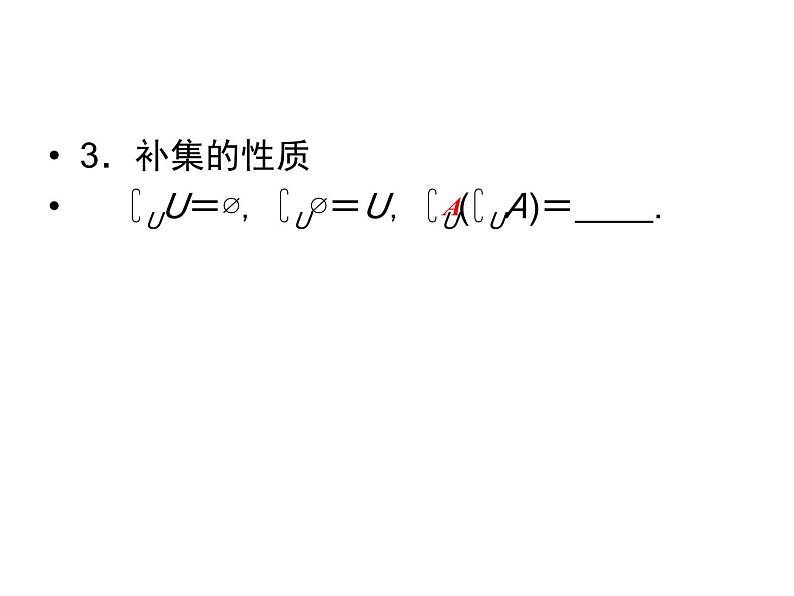
高中数学1.1 集合的概念教案配套课件ppt

这是一份高中数学1.1 集合的概念教案配套课件ppt，共27页。PPT课件主要包含了所有元素，不属于集合A，∁UA等内容，欢迎下载使用。

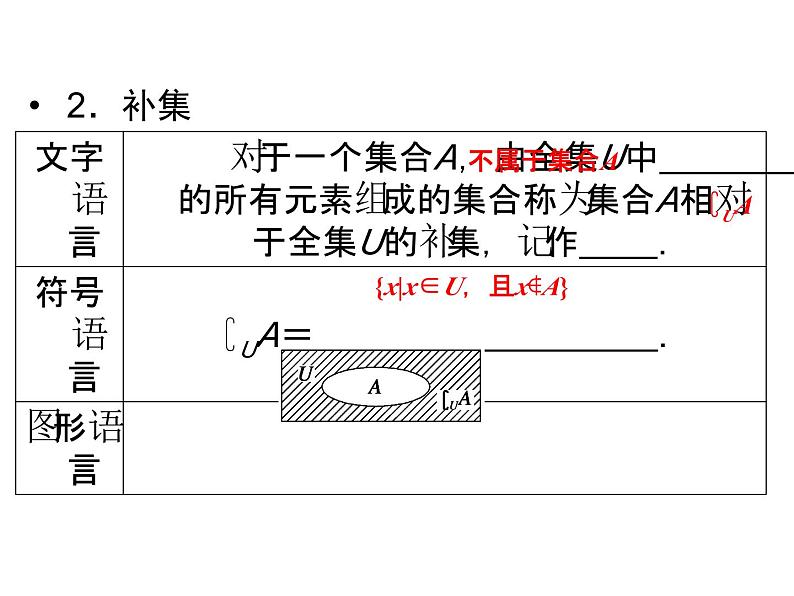
新知导学1．全集(1)定义：如果一个集合含有我们所研究问题中涉及的 ，那么就称这个集合为全集．(2)记法：全集通常记作 .
{x|x∈U，且x∉A}
温馨提示：(1)补集是集合之间的一种运算．求集合A的补集的前提是A是全集U的子集，随着所选全集的不同，得到的补集也是不同的．(2)∁UA的数学意义包括两个方面：首先必须具备A⊆U；其次是定义∁UA＝{x|x∈U，且x∉A}．
3．补集的性质∁UU＝∅，∁U∅＝U，∁U(∁UA)＝ .
互动探究探究点1 全集一定包含任何一个元素吗？若全集是数集，则一定是实数集R吗？提示　全集仅包含我们研究问题所涉及的全部元素，而非任何元素，我们研究的问题并不一定是实数集，也有可能为整数集、自然数集或有理数集等等．探究点2 ∁AC与∁BC相等吗？提示　不一定相等．当A＝B时，二者相等，否则不相等．探究点3 集合A与集合A在全集U中的补集有公共元素吗？提示　没有，A∩(∁UA)＝∅.
类型一　补集的运算【例1】 (1)已知全集U＝{0,1,2,3,4}，集合A＝{1,2,3}，B＝{2,4}，则(∁UA)∪B为(　　)．A．{1,2,4} B．{2,3,4}C．{0,2,4} D．{0,2,3,4}(2)设全集U＝R，集合A＝{x|x≥－3}，B＝{x|－3 [思路探索]　依补集的意义，由定义或Venn图求解．(1)解析　由U＝{0,1,2,3,4}，A＝{1,2,3}．∴∁UA＝{0,4}，从而(∁UA)∪B＝{0,2,4}，选C.答案　C (2)解　①∵A＝{x|x≥－3}，∴∁UA＝∁RA＝{x|x<－3}．又∵B＝{x|－32}．②由数轴可知：显然，∁UA ∁UB.
[规律方法]　1.如果所给集合是有限集，则先把集合中的元素一一列举出来，然后结合补集的定义来求解，并注意借助Venn图．2．如果所给集合是无限集，则常借助于数轴，把已知集合及全集分别表示在数轴上，然后再根据补集的定义求解，这样处理比较形象直观，解答过程中注意边界问题．
【活学活用1】 设U＝{x|－5≤x＜－2，或2＜x≤5，x∈Z}，A＝{x|x2－2x－15＝0}，B＝{－3,3,4}，求∁UA、∁UB.解　∵U＝{x|－5≤x＜－2，或2＜x≤5，x∈Z} ＝{－5，－4，－3,3,4,5}，又∵A＝{x|x2－2x－15＝0}＝{－3,5}．由补集的定义知：∁UA＝{－5，－4,3,4}，∁UB＝{－5，－4,5}．
类型二　补集的应用【例2】 已知全集U＝R，集合A＝{x|x＜－1}，B＝{x|2a＜x＜a＋3}，且B⊆∁RA，求a的取值范围．[思路探索]　可先求出∁RA，再结合B⊆∁RA列出关于a的不等式组求a的取值范围．
[规律方法]　解答本题的关键是利用B⊆∁UA，对B＝∅与B≠∅进行分类讨论，转化为与之等价的不等式(组)求解．不等式中的等号在补集中能否取到，要引起重视，注意检验．
【活学活用2】 设U＝{0,1,2,3}，A＝{x∈U|x2＋mx＝0}，若∁UA＝{1,2}，则实数m＝________.解析　∵U＝{0,1,2,3}，∁UA＝{1,2}，∴A＝{0,3}．又0,3是方程x2＋mx＝0的两根，∴m＝－3.答案　－3
[规律方法]　1.在第(2)问中，易误认为“∁UA＝B，∁UB＝A”导致逻辑错误．2．进行集合的交、并、补运算时应紧扣定义，适当借助Venn图及数轴等工具．
【活学活用3】 设全集为R，A＝{x|3≤x<7}，B＝{x|2方法技巧　补集思想的应用 有些数学问题，若直接从正面解决，或解题思路不明朗，或需要考虑的因素太多，可用补集思想考虑其对立面，即从结论的反面去思考，探索已知和未知之间的关系，从而化繁为简，化难为易，开拓解题思路．
【示例】 已知集合A＝{y|y＞a2＋1，或y＜a}，B＝{y|2≤y≤4}，若A∩B≠∅，求实数a的取值范围．[思路分析]　由于集合A包含两个不等式，若直接利用交集不为空集求解，则分情况较多，因此考虑从交集为空集的角度入手．
2．设全集U＝M∪N＝{1,2,3,4,5}，M∩∁UN＝{2,4}，则N＝(　　)．A．{1,2,3} B．{1,3,5}C．{1,4,5} D．{2,3,4}解析　∵M∩∁UN＝{2,4}，∴元素2,4是∁UN中的元素，即2,4一定不是N中的元素，故A、C、D错误．答案　B
4．已知全集U＝{2,5,8}，且∁UA＝{2}，则集合A的真子集有________个．解析　∵∁UA＝{2}，∴A＝{5,8}，A的真子集为{5}，{8}，∅共3个．答案　3