2023七年级数学下册第五章生活中的轴对称测试题新版北师大版

这是一份2023七年级数学下册第五章生活中的轴对称测试题新版北师大版，共5页。

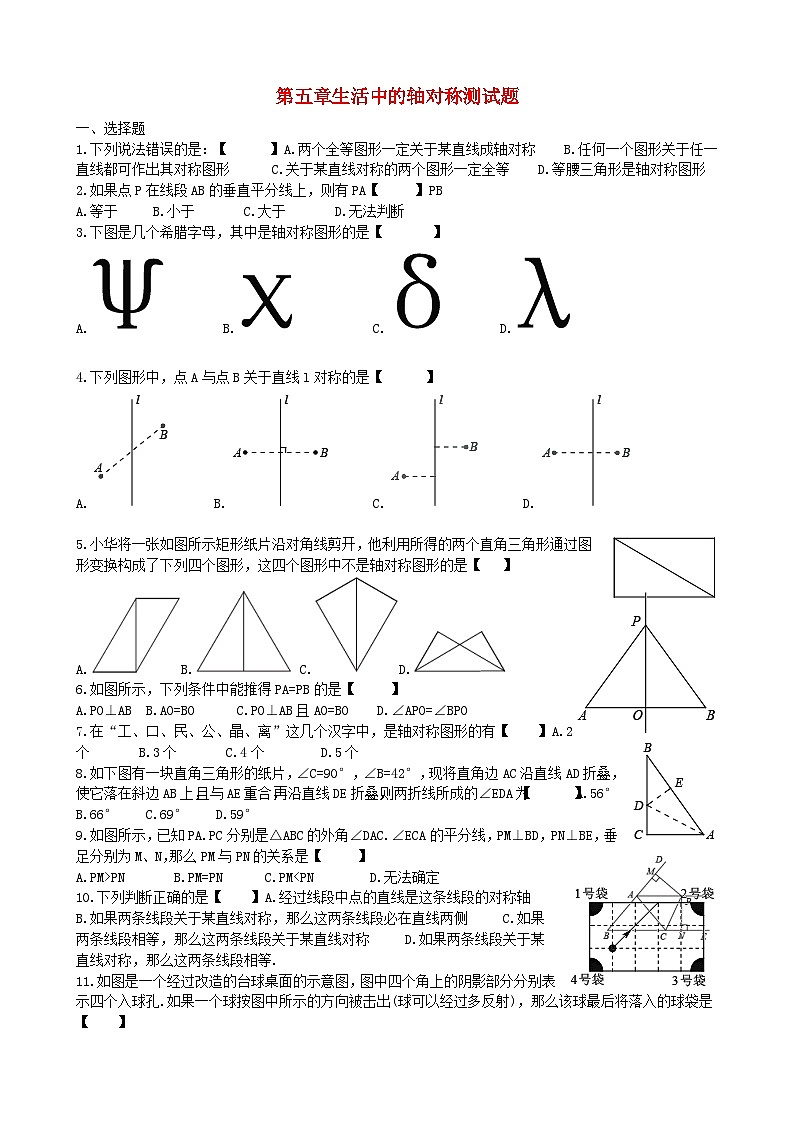
第五章生活中的轴对称测试题
一、选择题
1.下列说法错误的是：【 】A.两个全等图形一定关于某直线成轴对称 B.任何一个图形关于任一直线都可作出其对称图形 C.关于某直线对称的两个图形一定全等 D.等腰三角形是轴对称图形
2.如果点P在线段AB的垂直平分线上，则有PA【 】PB
A.等于　 　B.小于　　 C.大于　　 D.无法判断
3.下图是几个希腊字母，其中是轴对称图形的是【 】
A. B. C. D.

4.下列图形中，点A与点B关于直线l对称的是【 】
A. B. C.　 D.

5.小华将一张如图所示矩形纸片沿对角线剪开，他利用所得的两个直角三角形通过图形变换构成了下列四个图形，这四个图形中不是轴对称图形的是【 】
A.B. C.D.
6.如图所示，下列条件中能推得PA=PB的是【 】
A.PO⊥AB　B.AO=BO C.PO⊥AB且AO=BO　　D.∠APO=∠BPO
7.在“工、口、民、公、晶、离”这几个汉字中，是轴对称图形的有【 】A.2个　 　B.3个 C.4个　 D.5个
8.如下图有一块直角三角形的纸片，∠C=90°，∠B=42°，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，再沿直线DE折叠，则两折线所成的∠EDA为【 】A.56° B.66° 　C.69° D.59°
9.如图所示，已知PA.PC分别是△ABC的外角∠DAC.∠ECA的平分线，PM⊥BD，PN⊥BE，垂足分别为M、N，那么PM与PN的关系是【 】
A.PM>PN 　B.PM=PN C.PM 10.下列判断正确的是【 】A.经过线段中点的直线是这条线段的对称轴 B.如果两条线段关于某直线对称，那么这两条线段必在直线两侧 C.如果两条线段相等，那么这两条线段关于某直线对称 D.如果两条线段关于某直线对称，那么这两条线段相等.
11.如图是一个经过改造的台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多反射)，那么该球最后将落入的球袋是【 】
A.1号袋 　B.2号袋　 C.3号袋　 D.4号袋
12.如图，直线表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有【 】
A.1处 　B.2处 　C.3处 　D.4处
二、填空题
13.如果一个图形沿一条直线对折，直线两旁的部分能互相重合，那么这个图形叫做_____________，这条直线是_______________________．
14.如图，AD是△ABC的中线，∠ADC=45°，将△ADC沿AD对折，点C落在C'处，则BD与DC'的大小关系是____________，位置关系是____________.
15.轴对称的两个图形的对应边、对应角_________________.
16.一个号码在镜子里的像如图所示，则这个号码是____________.
17.如图，将△ABC沿着DE翻折，若∠1+∠2=80°，则∠B=_________.
18.在Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，如果BC=40cm，BD:CD=5:3，那么点D到AB的距离是______cm.
19.如图，在四边形ABCD中，∠A=90°，AD=4，连接BD，BD⊥CD，∠ADB=∠C．若P是BC边上一动点，则DP长的最小值为_ __.
20.如图，一束光线与水平镜面的夹角为α，该光线先照射到平面镜上，然后在两个平面镜上反射.如果∠α=60°，∠β=50°，那么∠γ=__________________.








三、解答题
21.如图所示，在△ABC中，AB=AC，DE垂直平分AB于点E，交AC于点D，若AB=6，BC=4，则求△BCD周长．







22.如下图所示，请你按要求用直尺(没有刻度)和圆规作图：
(1)作射线AM；(2)在射线AM上截取AB=a；(3)分别以点A.B为圆心，以大于a的一半的长度为半径画弧，弧相交于两点C.D；(4)连接CD，交AB于点P. 你得到的点P与线段AB有什么关系？
23.图中的正方形是8个全等的等腰直角三角形拼成的，试问：三角形①与哪些三角形成轴对称？将它们写出来，并指明相应的对称轴.








四、证明题
24.如图，∠C=90°，∠1=∠2.若AC=10，AD=6，求点D到边AB的距离.








25.如图所示，D是∠ABC的角平分线上一点，点P在BD上，PA⊥AB，PC⊥BC，垂足为A.C．求证：AD=CD，∠ADB=∠CDB．







五、作图题
26.如图，已知线段AB，用直尺和圆规作AB的垂直平分线l.






27.如图，方格中只画出了以虚线l为对称轴的轴对称图形的一半，请把另一半图形补画出来.







28.在3×3的正方形格点图中，有格点△ABC和△DEF，且△ABC和△DEF关于某直线成轴对称，请在下面的备用图中画出所有这样的△DEF.

六、应用题
29.在旷野上，一个人骑马从A到B，在行程中他必须让马在河边饮水一次，如图所示，他应怎样选择饮水点P，才能使所走的路程PA+PB最短？


参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
A
A
B
A
C
B
B
B
D
B
D
二、填空题
题号
13
14
15
16
17
18
19
20
答案
轴对称图形；对称轴
相等；垂直
相等
2502或2052
40°
15
4
40
三、解答题

21)、1.∵DE垂直平分AB于点E，
∴BD=AD，
∴△BCD的周长=BC+CD+DB=BC+AD+CD=BC+AC.
∵AB=AC，
∴△BCD的周长=BC+AB.
∵AB=6，BC=4，
∴△BCD的周长=4+6=10.
22)、【解答】1.画出的图形如图所示，通过测量可知，得到的点P是线段AB的中点.
23)、1.①与②成轴对称，对称轴是AC所在的直线；①与④成轴对称，对称轴是HF所在的直线；①与⑧成轴对称，对称轴是EG所在的直线；①与⑥成轴对称，对称轴是BD所在的直线.
24)、【解答】1.作DE⊥AB于E，
因为∠1=∠2，∠C=90°，
所以CD=DE.
因为CD=AC-AD=10-6=4，
所以DE=4.
25)、【解答】1.∵BP是∠ABC的角平分线，PA⊥AB，PC⊥BC，
∴∠APB=∠CPB，PA=PC．
则有
∴△ADP≌△CDP(SAS)．
∴AD=CD，∠ADP=∠CDP．
∴∠ADB=∠CDB．
26)【解答】1.(1)分别以点A.B为圆心，大于长为半径画弧，两弧相交于C.D两点.
(2)过点C.D作直线l，直线l就是线段AB的垂直平分线.
27)、【解答】1.如图，利用方格纸找有关点关于直线l的对称点，再连线完成图28)、
【解答】1.如下图所示：

【点评】确定对称轴是画图的前提和关键，要能灵活运用正方形的对称性.
29)、【解答】1.解：如图所示.
(1)作点A关于l的对称点A'；
(2)连接A'B，交l于点P，则P点即为所求.
【点评】在解此题时应先利用轴对称把两条线段转化到同一直线上，再利用“两点之间线段最短”这一特性来求