初中华师大版3. 切线同步训练题

  27．2.3.1 切线的判定和性质

1．下列直线中能判定为圆的切线的是(　　)

A．与圆有公共点的直线

B．过圆的半径外端的直线

C．垂直于圆的半径且与圆有公共点的直线

D．过半径的外端且与半径垂直的直线

2．如图，在平面直角坐标系中，过格点A，B，C作一圆弧，点B与下列格点的连线中，能够与该圆弧相切的是(　　)

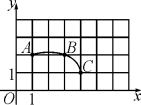
A．点D1(0，3)　 B．点D2(2，3)    C．点D3(5，1)     D．点D4(6，1)

3. 如图，AB是⊙O的直径，BC交⊙O于点D，DE⊥AC于点E，要使DE是⊙O的切线，还需补充一个条件，则补充的条件不正确的是(　　)

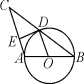
A．DE＝DO   B．AB＝AC    C．CD＝DB   D．AC∥OD

4. 如图，△ABC的边AC与⊙O相交于C，D两点，且经过圆心O，边AB与⊙O相切，切点为B.已知∠A＝30°，则∠C的大小是(　　)

A．30°     B．45°    C．60°     D．40°

5．如图，AB是⊙O的切线，B为切点，AO与⊙O交于点C，若∠BAO＝40°，则∠OCB的度数为(　　)

A．40°      B．50°    C．65°      D．75°

6. 如图，AB是⊙O直径，点C在AB的延长线上，CD切⊙O于点D，连接AD，若∠A＝25°，则∠C的大小为____°.

7. 如图，点A在⊙O上，下列条件不能说明PA是⊙O的切线的是(　　)

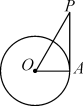
A．OA2＋PA2＝OP2　　B．PA⊥OA      C．∠P＝30°，∠O＝60°      D．OP＝2OA

8. 如图，P是⊙O外一点，PA是⊙O的切线，PO＝26 cm，PA＝24 cm，则⊙O的周长为(　　)

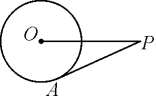
A．18π cm　　 B．16π cm     C．20π cm     D．24π cm

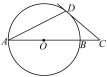
9. 如图，AB是⊙O的直径，C，D是⊙O上的点，∠CDB＝20°，过点C作⊙O的切线交AB的延长线于点E，则∠E等于(　　)

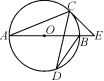
A．40°  B．50°  C．60°  D．70°

10. 如图，点A，B，D在⊙O上，∠A＝25°，OD的延长线交直线BC于点C，且∠OCB＝40°，直线BC与⊙O的位置关系为___________________．

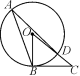
11．如图，A，B是⊙O上的两点，AC是过A点的一条直线，如果∠AOB＝120°，那么当∠CAB的度数等于___________________度时，AC才能成为⊙O的切线．

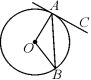
12. 如图，一个边长为4 cm的等边三角形ABC的高与⊙O的直径相等．⊙O与BC相切于点C，与AC相交于点E，则CE的长为_________cm.

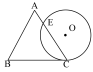
13. 如图，在△ABC中，AB＝AC，点O在边AB上，⊙O过点B且分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F，求证：直线EF是⊙O的切线．

14. )如图，⊙O的半径为4，B是⊙O外一点，连接OB，且OB＝6，过点B作⊙O的切线BD，切点为D，延长BO交⊙O于点A，过点A作切线BD的垂线，垂足为C.

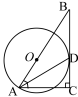
(1)求证：AD平分∠BAC；

(2)求AC的长．

答案：

1.  D

2.  C

3.  A

4.  A

5.  C

6.  40

7.  D

8.  C

9.  B

10. 相切

11.  60

12.  3

13. 解：连接OE，DE，∵BD是⊙O的直径，∴∠DEB＝90°，∵AB＝AC，∴∠ABC＝∠C，又∵OB＝OE，∴∠ABC＝∠OEB，∵∠FEC＋∠C＝90°，∴∠FEC＋∠OEB＝90°，∴OE⊥EF，∵OE是⊙O半径，∴直线EF是⊙O的切线

14.