




还剩51页未读,
继续阅读
所属成套资源:2024秋新人教版数学九年级上学期课件PPT整套
成套系列资料,整套一键下载
人教版数学九年级上册22.1.4《二次函数y=ax%U00B2+bx+c的图象和性质》(第1课时 )课件
展开
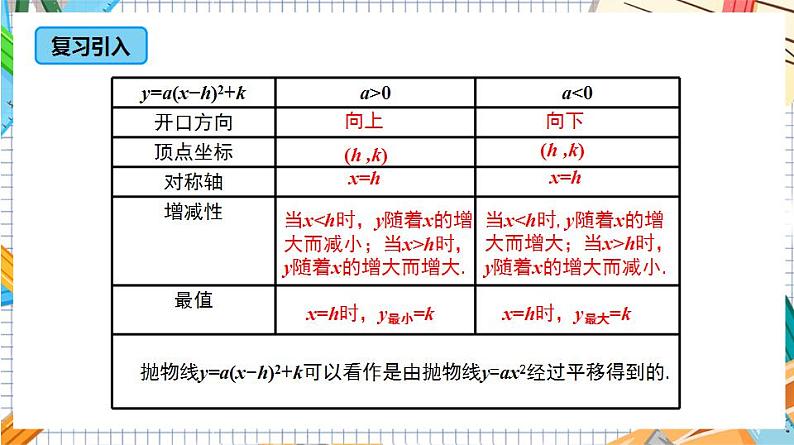
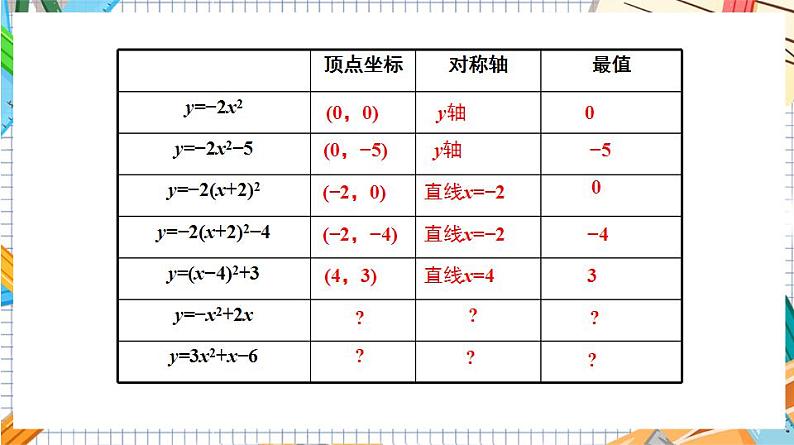
22.1.4二次函数y=ax2+bx+c的图象和性质(第1课时 )第22章二次函数人教版数学九年级上册目录情境引入1.会用配方法或公式法将一般式y=ax2+bx+c化成顶点式y=a(x−h)2+k(a≠0).(难点)2.会熟练求出二次函数一般式y=ax2+bx+c(a≠0)的顶点坐标、对称轴.(重点)复习引入向上向下(h ,k)(h ,k)x=hx=h当xh时,y随着x的增大而增大. 当xh时,y随着x的增大而减小. x=h时,y最小=kx=h时,y最大=k抛物线y=a(x−h)2+k可以看作是由抛物线y=ax2经过平移得到的.(0,0)y轴0(0,−5)y轴−5(−2,0)直线x=−20(−2,−4)直线x=−2−4(4,3)直线x=43??????合作探究(1)x2-12x+36=_____________;填一填(2)x2-12x=_____________ .(x−6)2(x−6)2−36(1)“提”:提出二次项系数;(2)“配”:括号内配成完全平方;(3)“化”:化成顶点式.想一想:配方的方法及步骤是什么?提示:配方后的表达式通常称为配方式或顶点式. 我们如何用配方法将一般式y=ax2+bx+c(a≠0)化成顶点式y=a(x−h)2+k?y=ax²+bx+c 将下列二次函数的一般式用配方法化成顶点式y=a(x-h)2+k的形式,并指出其顶点坐标.(1)y=x2-2x+1;(2)y=2x2-4x+6.练一练解:(1)y=x2−2x+1=(x−1)2,顶点坐标为(1,0);(2)y=2x2−4x+6=2(x−1)2+4,顶点坐标为(1,4).探究归纳答:对称轴是直线x=6,顶点坐标是(6,3).答:平移方法1: 先向上平移3个单位,再向右平移6个单位得到的; 平移方法2: 先向右平移6个单位,再向上平移3个单位得到的.问题3 如何画二次函数 的图象?先利用图形的对称性列表7.553.533.557.5然后描点画图,得到图象如右图.O问题4 结合二次函数 的图象,说出其性质.x=6当x<6时,y随x的增大而减小;当x>6时,y随x的增大而增大.O归纳总结二次函数y=ax2+bx+c的图象和性质(1)(2)如果a>0,当x< 时,y随x的增大而减小;当x> 时,y随x的增大而增大.如果a<0,当x< 时,y随x的增大而增大;当x> 时,y随x的增大而减小. −15−513 典例精析1−5−15然后描点、连线,得到图象如下图.由图象可知,这个函数具有如下性质:当x<-1时,函数值y随x的增大而增大;当x>-1时,函数值y随x的增大而减小;当x=-1时,函数取得最大值,最大值y=3.练一练 已知二次函数y=x2﹣6x+5.(1)将y=x2﹣6x+5化成y=a(x﹣h)2+k的形式;(2)求该二次函数的图象的对称轴和顶点坐标;(3)当x取何值时,y随x的增大而减小.(3)∵抛物线的开口向上,对称轴是x=3,∴当x≤3时,y随x的增大而减小.解:(1)y=x2﹣6x+5=(x﹣3)2﹣4.(2)二次函数的图象的对称轴是x=3,顶点坐标是(3,﹣4).合作探究问题1 一次函数y=kx+b的图象如下图所示,请根据一次函数图象的性质填空:<>><>>问题2 二次函数 的图象如下图所示,请根据二次函数的性质填空:>>>><=x=0时,y=c.>0<0<=><><x=0时,y=c.二次函数y=ax2+bx+c的图象与a、b、c的关系向上向下y左右正负例2 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2. 其中正确的个数是 ( )A.1 B.2 C.3 D.4D 由图象上横坐标为 x=-2的点在第三象限可得4a-2b+c<0,故③正确; 由图象上x=1的点在第四象限得a+b+c<0,由图象上x=-1的点在第二象限得出 a-b+c>0,则(a+b+c)(a-b+c)<0,即(a+c)2-b2<0,可得(a+c)2<b2,故④正确.【解析】由图象开口向下可得a<0,由对称轴在y轴左侧可得b<0,由图象与y轴交于正半轴可得 c>0,则abc>0,故①正确;由对称轴x>-1可得2a-b<0,故②正确;1.【中考·济宁】将抛物线y=x2-6x+5向上平移两个单位,再向右平移1个单位后,得到的抛物线的表达式是( )A.y=(x-4)2-6 B.y=(x-1)2-3C.y=(x-2)2-2 D.y=(x-4)2-2D2.【2020·孝感】将抛物线C1:y=x2-2x+3向左平移1个单位长度,得到抛物线C2,抛物线C2与抛物线C3关于x轴对称,则抛物线C3的表达式为( )A.y=-x2-2 B.y=-x2+2C.y=x2-2 D.y=x2+2A3.【中考·重庆】抛物线y=-3x2+6x+2的对称轴是( )A.直线x=2 B.直线x=-2C.直线x=1 D.直线x=-1C4.【2020·温州】已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则( )A.y3<y2<y1 B.y3<y1<y2C.y2<y3<y1 D.y1<y3<y2B5.【2020·河北】如图,现要在抛物线y=x(4-x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是( )A.乙错,丙对 B.甲和乙都错C.乙对,丙错 D.甲错,丙对【点拨】y=x(4-x)=-x2+4x=-(x-2)2+4,∴抛物线的顶点坐标为(2,4),∴在抛物线上的点P的纵坐标最大为4,∴甲、乙的说法正确;若b=3,则抛物线上纵坐标为3的点有2个,∴丙的说法不正确;故选C.【答案】C6.【中考·温州】已知二次函数y=x2-4x+2,关于该函数在-1≤x≤3的取值范围内,下列说法正确的是( )A.有最大值-1,有最小值-2B.有最大值0,有最小值-1C.有最大值7,有最小值-1D.有最大值7,有最小值-2D7.【中考·成都】在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图所示,下列说法正确的是( )A.abc<0,b2-4ac>0 B.abc>0,b2-4ac>0C.abc<0,b2-4ac<0 D.abc>0,b2-4ac<0B【点拨】由y=ax2+bx+c的图象可知a<0,b>0,c<0,所以C选项符合题意,故选C.【答案】C*9.【2020·泰安】在同一平面直角坐标系内,二次函数y=ax2+bx+b(a≠0)与一次函数y=ax+b的图象可能是( )【点拨】根据二次函数图象的开口方向以及对称轴与y轴的关系即可得出a,b的正负,由此即可得出一次函数图象经过的象限,再与函数图象进行对比即可得出结论,故选C.【答案】CA12.【2020·温州】已知抛物线y=ax2+bx+1经过点(1,-2),(-2,13).(1)求a、b的值;(2)若(5,y1),(m,y2)是抛物线上不同的两点,且y2=12-y1,求m的值.解:由(1)得函数表达式为y=x2-4x+1,把点(5,y1)的坐标代入y=x2-4x+1中,得y1=6,∴y2=12-y1=6.∴y1=y2.又∵抛物线的对称轴为直线x=2,∴m=-1.13.【2020·河南】如图,抛物线y=-x2+2x+c与x轴正半轴,y轴正半轴分别交于点A、B,且OA=OB,点G为抛物线的顶点. (1)求抛物线的表达式及点G的坐标;解:∵抛物线y=-x2+2x+c与x轴正半轴,y轴正半轴分别交于点A、B,∴点B(0,c),∵OA=OB=c,∴点A(c,0),∴0=-c2+2c+c,∴c=3或c=0(舍去),∴抛物线的表达式为y=-x2+2x+3.∵y=-x2+2x+3=-(x-1)2+4,∴点G的坐标为(1,4).(2)点M、N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点M、N之间(含点M、N)的一个动点,求点Q的纵坐标yQ的取值范围.解:∵y=-x2+2x+3=-(x-1)2+4,∴对称轴为直线x=1,∵点M、N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,∴点M的横坐标为-2或4,点N的横坐标为6,∴点M坐标为(-2,-5)或(4,-5),点N坐标为(6,-21),∵点Q为抛物线上点M、N之间(含点M、N)的一个动点,∴-21≤yQ≤4或-21≤yQ≤-5. 14.【中考·台州】已知函数y=x2+bx+c(b、c为常数)的图象经过点(-2,4).(1)求b、c满足的关系式;解:将点(-2,4)的坐标代入y=x2+bx+c,得4-2b+c=4,∴c=2b. (2)设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数表达式; (3)若该函数的图象不经过第三象限,当-5≤x≤1时,函数的最大值与最小值之差为16,求b的值.【点拨】本题利用分段讨论法,将b的值分成几段进行讨论.顶点:对称轴:y=ax2+bx+c(a ≠0)(一般式)配方法公式法课堂小结THANKS“”
相关资料
更多









