

高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用教学设计及反思
展开第六章 平面向量及其应用
6.4 平面向量的应用
6.4.1 平面几何中的向量方法
教学设计
一、教学目标
- 掌握用向量方法解决平面几何问题;
- 体会向量在解决数学和实际问题中的作用.
二、教学重难点
- 教学重点
用向量方法解决实际问题的基本方法,向量法解决几何问题的“三步曲”.
- 教学难点
将实际问题转化为向量问题.
三、教学过程
(一) 新课导入
复习:(1)向量加法的三角形法则、平行四边形法则;
(2)向量平行、垂直的判断方法;
在之前向量的学习中,我们发现,平面几何图形的很多性质都可以用向量表示出来.因此平面几何中的许多问题都可以用向量运算的方法加以解决.下面我们通过例题,探究向量方法在平面几何中的应用.
(二)探索新知
例1 如图,DE是△ABC的中位线,用向量方法证明:![]() ,
,![]()
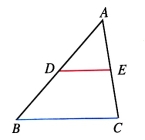
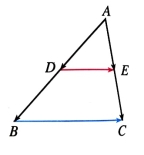 证明:如图,因为DE是△ABC的中位线,
证明:如图,因为DE是△ABC的中位线,
所以![]() ,
,![]() .
.
从而![]()
又![]() ,
,
所以![]() .
.
于是![]() ,
,![]()
用向量方法解决平面几何问题的“三步曲”:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何关系.
例2 如图,已知平行四边形ABCD,你能发现对角线AC和BD的长度与两条邻边AB和AD的长度之间的关系吗?
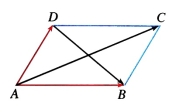
解:第一步,建立平面几何与向量的联系,用向量表示问题中的几何元素,将平面几何问题转化为向量问题:
 如图,取
如图,取![]() 为基底,设
为基底,设![]() ,则
,则
![]() ,
,![]() .
.
第二步,通过向量运算,研究几何元素之间的关系:
![]() ,
,
![]() .
.
上面两式相加,得![]() .
.
第三步,把运算结果“翻译”成几何关系:
![]() .
.
(三)课堂练习
- 已知P是
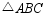 内的一点,
内的一点, ,则
,则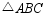 的面积与
的面积与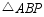 的面积的比值为( )
的面积的比值为( )
A.![]() B.2 C.3 D.6
B.2 C.3 D.6
答案:C
解析:在![]() 中,设边
中,设边![]() 的中点为D,则
的中点为D,则![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .故选C.
.故选C.
- 在
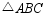 中,
中,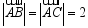 ,且
,且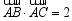 ,则
,则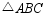 的形状是___________.
的形状是___________.
答案:等边三角形
解析:因为![]() ,所以
,所以![]() ,
,
又![]() 为
为![]() 的内角,所以
的内角,所以![]() .
.
又![]() ,所以
,所以![]() 为等边三角形.
为等边三角形.
答案:2
解析: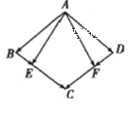
如图, ![]() ,
,
![]() ,
,
由题意知![]() ,
,
所以![]()
![]()
![]() ,
,
解得![]() .
.
(四) 小结作业
小结:
- 用向量方法解决平面几何问题的“三步曲”;
- 用向量方法解决平面几何问题的应用.
作业:
四、板书设计
6.4.1 平面几何中的向量方法
用向量方法解决平面几何问题的“三步曲”.
高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用教案设计: 这是一份高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用教案设计,共4页。
人教A版 (2019)必修 第二册第六章 平面向量及其应用6.4 平面向量的应用教学设计: 这是一份人教A版 (2019)必修 第二册第六章 平面向量及其应用6.4 平面向量的应用教学设计,共4页。教案主要包含了教学目标,教学重难点,教学过程,作业等内容,欢迎下载使用。
人教A版 (2019)必修 第二册6.4 平面向量的应用教案: 这是一份人教A版 (2019)必修 第二册6.4 平面向量的应用教案,共5页。教案主要包含了教学目标,教学重难点,教学过程,课外作业等内容,欢迎下载使用。













