湖北省随州市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类

这是一份湖北省随州市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类，共42页。

湖北省随州市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类
一．二次函数的应用（共1小题）
1．（2022•随州）2022年的冬奥会在北京举行，其中冬奥会吉祥物“冰墩墩”深受人们喜爱，多地出现了“一墩难求”的场面．某纪念品商店在开始售卖当天提供150个“冰墩墩”后很快就被抢购一空，该店决定让当天未购买到的顾客可通过预约在第二天优先购买，并且从第二天起，每天比前一天多供应m个（m为正整数）．经过连续15天的销售统计，得到第x天（1≤x≤15，且x为正整数）的供应量y1（单位：个）和需求量y2（单位：个）的部分数据如下表，其中需求量y2与x满足某二次函数关系．（假设当天预约的顾客第二天都会购买，当天的需求量不包括前一天的预约数）
第x天
1
2
…
6
…
11
…
15
供应量y1（个）
150
150+m
…
150+5m
…
150+10m
…
150+14m
需求量y2（个）
220
229
…
245
…
220
…
164
（1）直接写出y1与x和y2与x的函数关系式；（不要求写出x的取值范围）
（2）已知从第10天开始，有需求的顾客都不需要预约就能购买到（即前9天的总需求量超过总供应量，前10天的总需求量不超过总供应量），求m的值；（参考数据：前9天的总需求量为2136个）
（3）在第（2）问m取最小值的条件下，若每个“冰墩墩”售价为100元，求第4天与第12天的销售额．
二．二次函数综合题（共3小题）
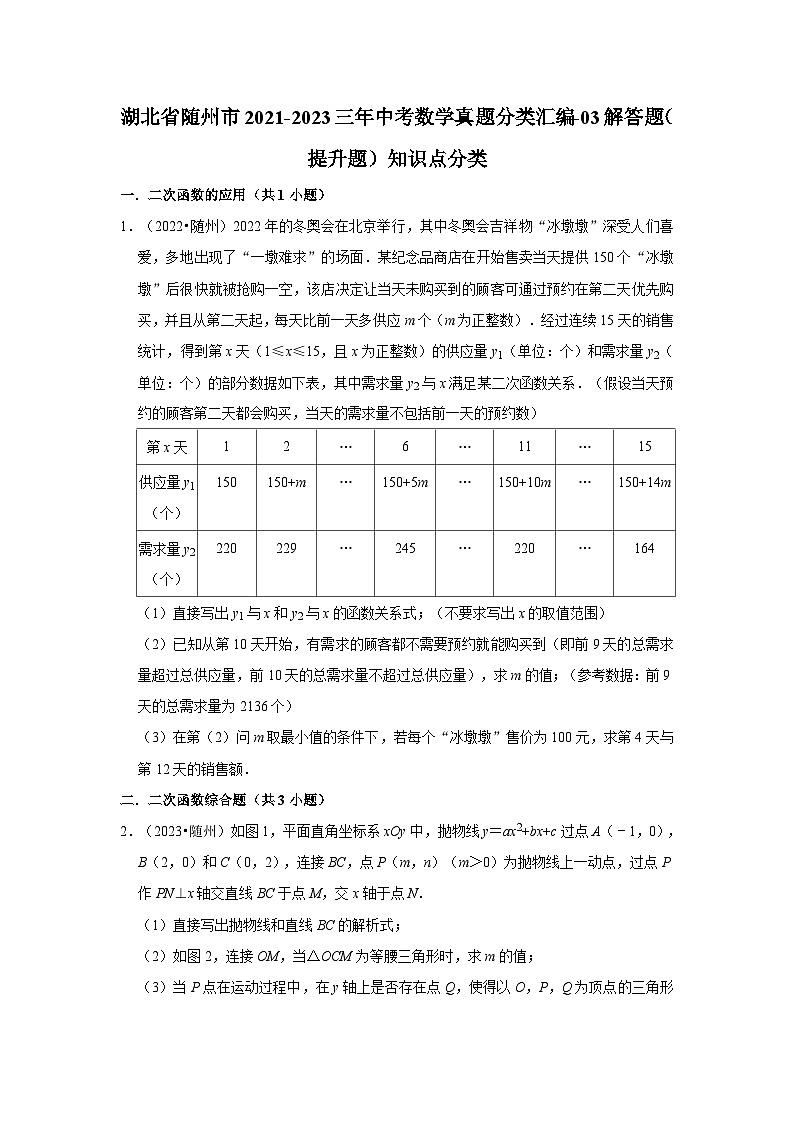
2．（2023•随州）如图1，平面直角坐标系xOy中，抛物线y＝ax2+bx+c过点A（﹣1，0），B（2，0）和C（0，2），连接BC，点P（m，n）（m＞0）为抛物线上一动点，过点P作PN⊥x轴交直线BC于点M，交x轴于点N．
（1）直接写出抛物线和直线BC的解析式；
（2）如图2，连接OM，当△OCM为等腰三角形时，求m的值；
（3）当P点在运动过程中，在y轴上是否存在点Q，使得以O，P，Q为顶点的三角形与以B，C，N为顶点的三角形相似（其中点P与点C相对应），若存在，直接写出点P和点Q的坐标；若不存在，请说明理由．

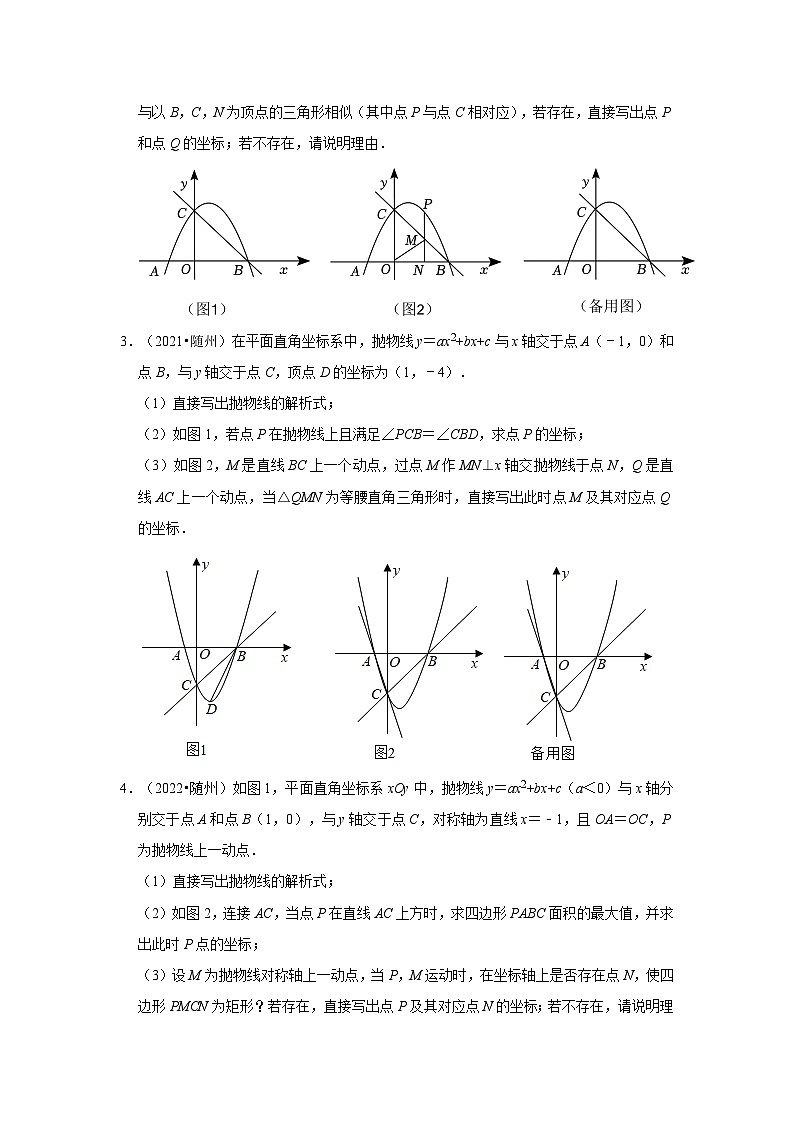
3．（2021•随州）在平面直角坐标系中，抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0）和点B，与y轴交于点C，顶点D的坐标为（1，﹣4）．
（1）直接写出抛物线的解析式；
（2）如图1，若点P在抛物线上且满足∠PCB＝∠CBD，求点P的坐标；
（3）如图2，M是直线BC上一个动点，过点M作MN⊥x轴交抛物线于点N，Q是直线AC上一个动点，当△QMN为等腰直角三角形时，直接写出此时点M及其对应点Q的坐标．

4．（2022•随州）如图1，平面直角坐标系xOy中，抛物线y＝ax2+bx+c（a＜0）与x轴分别交于点A和点B（1，0），与y轴交于点C，对称轴为直线x＝﹣1，且OA＝OC，P为抛物线上一动点．
（1）直接写出抛物线的解析式；
（2）如图2，连接AC，当点P在直线AC上方时，求四边形PABC面积的最大值，并求出此时P点的坐标；
（3）设M为抛物线对称轴上一动点，当P，M运动时，在坐标轴上是否存在点N，使四边形PMCN为矩形？若存在，直接写出点P及其对应点N的坐标；若不存在，请说明理由．


三．矩形的性质（共1小题）
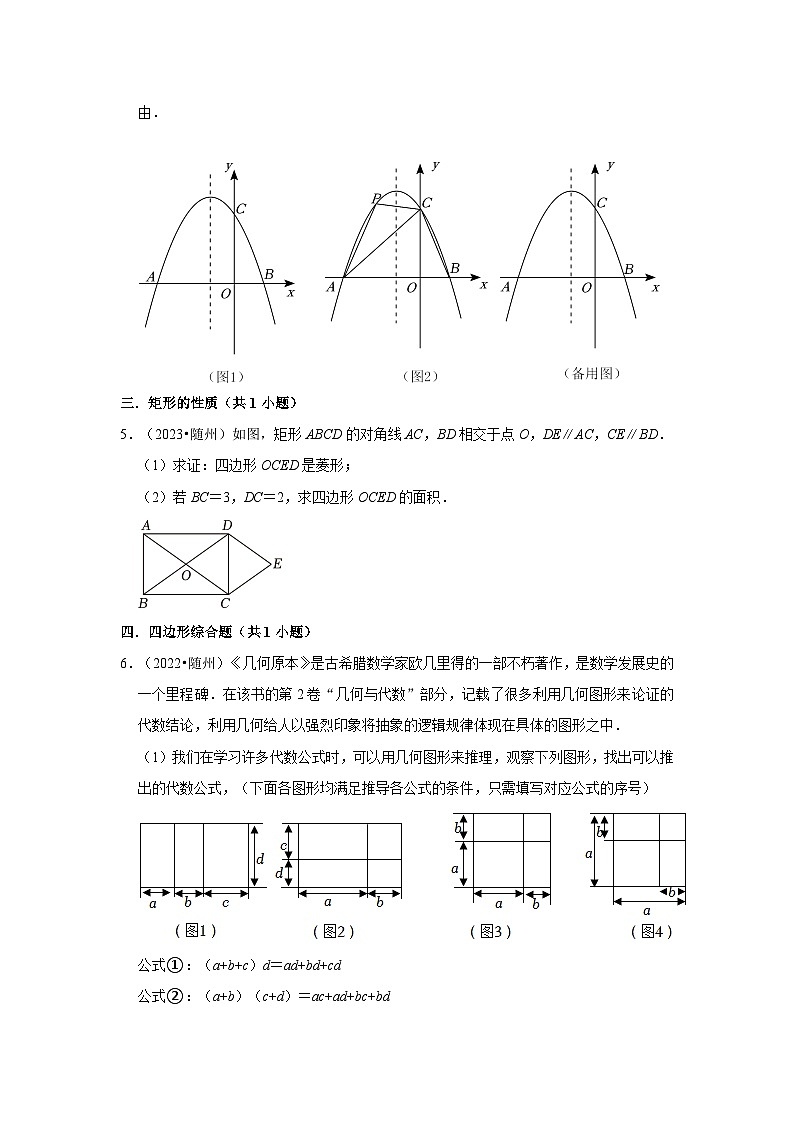
5．（2023•随州）如图，矩形ABCD的对角线AC，BD相交于点O，DE∥AC，CE∥BD．
（1）求证：四边形OCED是菱形；
（2）若BC＝3，DC＝2，求四边形OCED的面积．

四．四边形综合题（共1小题）
6．（2022•随州）《几何原本》是古希腊数学家欧几里得的一部不朽著作，是数学发展史的一个里程碑．在该书的第2卷“几何与代数”部分，记载了很多利用几何图形来论证的代数结论，利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中．
（1）我们在学习许多代数公式时，可以用几何图形来推理，观察下列图形，找出可以推出的代数公式，（下面各图形均满足推导各公式的条件，只需填写对应公式的序号）

公式①：（a+b+c）d＝ad+bd+cd
公式②：（a+b）（c+d）＝ac+ad+bc+bd
公式③：（a﹣b）2＝a2﹣2ab+b2
公式④：（a+b）2＝a2+2ab+b2
图1对应公式 　 　，图2对应公式 　 　，图3对应公式 　 　，图4对应公式 　 　．
（2）《几何原本》中记载了一种利用几何图形证明平方差公式（a+b）（a﹣b）＝a2﹣b2的方法，如图5，请写出证明过程；（已知图中各四边形均为矩形）
（3）如图6，在等腰直角三角形ABC中，∠BAC＝90°，D为BC的中点，E为边AC上任意一点（不与端点重合），过点E作EG⊥BC于点G，作EH⊥AD于点H，过点B作BF∥AC交EG的延长线于点F．记△BFG与△CEG的面积之和为S1，△ABD与△AEH的面积之和为S2．
①若E为边AC的中点，则的值为 　 　；
②若E不为边AC的中点时，试问①中的结论是否仍成立？若成立，写出证明过程；若不成立，请说明理由．

五．切线的性质（共2小题）
7．（2022•随州）如图，已知D为⊙O上一点，点C在直径BA的延长线上，BE与⊙O相切，交CD的延长线于点E，且BE＝DE．
（1）判断CD与⊙O的位置关系，并说明理由；
（2）若AC＝4，sinC＝，
①求⊙O的半径；
②求BD的长．

8．（2021•随州）如图，D是以AB为直径的⊙O上一点，过点D的切线DE交AB的延长线于点E，过点B作BC⊥DE交AD的延长线于点C，垂足为点F．
（1）求证：AB＝BC；
（2）若⊙O的直径AB为9，sinA＝．
①求线段BF的长；
②求线段BE的长．

六．切线的判定与性质（共1小题）
9．（2023•随州）如图，AB是⊙O的直径，点E，C在⊙O上，点C是的中点，AE垂直于过C点的直线DC，垂足为D，AB的延长线交直线DC于点F．
（1）求证：DC是⊙O的切线；
（2）若AE＝2，sin∠AFD＝，
①求⊙O的半径；
②求线段DE的长．

七．圆的综合题（共1小题）
10．（2021•随州）等面积法是一种常用的、重要的数学解题方法．它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题，在解题中，灵活运用等面积法解决相关问题，可以使解题思路清晰，解题过程简便快捷．
（1）在直角三角形中，两直角边长分别为3和4，则该直角三角形斜边上的高的长为 　 　，其内切圆的半径长为 　 　；
（2）①如图1，P是边长为a的正△ABC内任意一点，点O为△ABC的中心，设点P到△ABC各边距离分别为h1，h2，h3，连接AP，BP，CP，由等面积法，易知a（h1+h2+h3）＝S△ABC＝3S△OAB，可得h1+h2+h3＝　 　；（结果用含a的式子表示）

②如图2，P是边长为a的正五边形ABCDE内任意一点，设点P到五边形ABCDE各边距离分别为h1，h2，h3，h4，h5，参照①的探索过程，试用含a的式子表示h1+h2+h3+h4+h5的值．（参考数据：tan36°≈，tan54°≈）
（3）①如图3，已知⊙O的半径为2，点A为⊙O外一点，OA＝4，AB切⊙O于点B，弦BC∥OA，连接AC，则图中阴影部分的面积为 　 　；（结果保留π）
②如图4，现有六边形花坛ABCDEF，由于修路等原因需将花坛进行改造，若要将花坛形状改造成五边形ABCDG，其中点G在AF的延长线上，且要保证改造前后花坛的面积不变，试确定点G的位置，并说明理由
八．几何变换综合题（共1小题）
11．（2023•随州）1643年，法国数学家费马曾提出一个著名的几何问题：给定不在同一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最小的点的位置，意大利数学家和物理学家托里拆利给出了分析和证明，该点也被称为“费马点”或“托里拆利点”，该问题也被称为“将军巡营”问题．
（1）下面是该问题的一种常见的解决方法，请补充以下推理过程：（其中①处从“直角”和“等边”中选择填空，②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空，③处填写角度数，④处填写该三角形的某个顶点）
当△ABC的三个内角均小于120°时，
如图1，将△APC绕点C顺时针旋转60°得到△A′P′C，连接PP′，
由PC＝P′C，∠PCP′＝60°，可知△PCP′为 　 　三角形，故PP′＝PC，又P′A′＝PA，故PA+PB+PC＝P′A′+PB+PP′≥A′B，
由 　 　可知，当B，P，P′，A′在同一条直线上时，PA+PB+PC取最小值，如图2，最小值为A′B，此时的P点为该三角形的“费马点”，
且有∠APC＝∠BPC＝∠APB＝　 　；
已知当△ABC有一个内角大于或等于120°时，“费马点”为该三角形的某个顶点．如图3，若∠BAC≥120°，则该三角形的“费马点”为 　 　点．
（2）如图4，在△ABC中，三个内角均小于120°，且AC＝3，BC＝4，∠ACB＝30°，已知点P为△ABC的“费马点”，求PA+PB+PC的值；

（3）如图5，设村庄A，B，C的连线构成一个三角形，且已知AC＝4km，BC＝2km，∠ACB＝60°．现欲建一中转站P沿直线向A，B，C三个村庄铺设电缆，已知由中转站P到村庄A，B，C的铺设成本分别为a元/km，a元/km，a元/km，选取合适的P的位置，可以使总的铺设成本最低为 　 　元．（结果用含a的式子表示）
九．解直角三角形的应用-仰角俯角问题（共1小题）
12．（2023•随州）某校学生开展综合实践活动，测量某建筑物的高度AB，在建筑物附近有一斜坡，坡长CD＝10米，坡角α＝30°，小华在C处测得建筑物顶端A的仰角为60°，在D处测得建筑物顶端A的仰角为30°．（已知点A，B，C，D在同一平面内，B，C在同一水平线上）
（1）求点D到地面BC的距离；
（2）求该建筑物的高度AB．

一十．列表法与树状图法（共1小题）
13．（2021•随州）疫苗接种初期，为更好地响应国家对符合条件的人群接种新冠疫苗的号召，某市教育部门随机抽取了该市部分七、八、九年级教师，了解教师的疫苗接种情况，得到如下统计表：

已接种
未接种
合计
七年级
30
10
40
八年级
35
15
a
九年级
40
b
60
合计
105
c
150
（1）表中，a＝　 　，b＝　 　，c＝　 　；
（2）由表中数据可知，统计的教师中接种率最高的是 　 　年级教师；（填“七”或“八”或“九”）
（3）若该市初中七、八、九年级一共约有8000名教师，根据抽样结果估计未接种的教师约有 　 　人；
（4）为更好地响应号召，立德中学从最初接种的4名教师（其中七年级1名，八年级1名，九年级2名）中随机选取2名教师谈谈接种的感受，请用列表或画树状图的方法，求选中的两名教师恰好不在同一年级的概率．

湖北省随州市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类
参考答案与试题解析
一．二次函数的应用（共1小题）
1．（2022•随州）2022年的冬奥会在北京举行，其中冬奥会吉祥物“冰墩墩”深受人们喜爱，多地出现了“一墩难求”的场面．某纪念品商店在开始售卖当天提供150个“冰墩墩”后很快就被抢购一空，该店决定让当天未购买到的顾客可通过预约在第二天优先购买，并且从第二天起，每天比前一天多供应m个（m为正整数）．经过连续15天的销售统计，得到第x天（1≤x≤15，且x为正整数）的供应量y1（单位：个）和需求量y2（单位：个）的部分数据如下表，其中需求量y2与x满足某二次函数关系．（假设当天预约的顾客第二天都会购买，当天的需求量不包括前一天的预约数）
第x天
1
2
…
6
…
11
…
15
供应量y1（个）
150
150+m
…
150+5m
…
150+10m
…
150+14m
需求量y2（个）
220
229
…
245
…
220
…
164
（1）直接写出y1与x和y2与x的函数关系式；（不要求写出x的取值范围）
（2）已知从第10天开始，有需求的顾客都不需要预约就能购买到（即前9天的总需求量超过总供应量，前10天的总需求量不超过总供应量），求m的值；（参考数据：前9天的总需求量为2136个）
（3）在第（2）问m取最小值的条件下，若每个“冰墩墩”售价为100元，求第4天与第12天的销售额．
【答案】（1）y1＝mx+150﹣m，y2＝﹣x2+12x+209；
（2）m的值为20或21；
（3）第4天的销售额为21000元，第12天的销售额为20900元．
【解答】解：（1）根据题意得：y1＝150+（x﹣1）m＝mx+150﹣m，
设y2＝ax2+bx+c，将（1，220），（2，229），（6，245）代入得：
，
解得，
∴y2＝﹣x2+12x+209；
（2）前9天的总供应量为150+（150+m）+（150+2m）+......+（150+8m）＝（1350+36m）个，
前10天的供应量为1350+36m+（150+9m）＝（1500+45m）个，
在y2＝﹣x2+12x+209中，令x＝10得y＝﹣102+12×10+209＝229，
∵前9天的总需求量为2136个，
∴前10天的总需求量为2136+229＝2365（个），
∵前9天的总需求量超过总供应量，前10天的总需求量不超过总供应量，
∴，
解得19≤m＜21，
∵m为正整数，
∴m的值为20或21；
（3）由（2）知，m最小值为20，
∴第4天的销售量即供应量为y1＝4×20+150﹣20＝210，
∴第4天的销售额为210×100＝21000（元），
而第12天的销售量即需求量为y2＝﹣122+12×12+209＝209，
∴第12天的销售额为209×100＝20900（元），
答：第4天的销售额为21000元，第12天的销售额为20900元．
二．二次函数综合题（共3小题）
2．（2023•随州）如图1，平面直角坐标系xOy中，抛物线y＝ax2+bx+c过点A（﹣1，0），B（2，0）和C（0，2），连接BC，点P（m，n）（m＞0）为抛物线上一动点，过点P作PN⊥x轴交直线BC于点M，交x轴于点N．
（1）直接写出抛物线和直线BC的解析式；
（2）如图2，连接OM，当△OCM为等腰三角形时，求m的值；
（3）当P点在运动过程中，在y轴上是否存在点Q，使得以O，P，Q为顶点的三角形与以B，C，N为顶点的三角形相似（其中点P与点C相对应），若存在，直接写出点P和点Q的坐标；若不存在，请说明理由．

【答案】（1）抛物线解析式：y＝﹣x2+x+2，直线BC：y＝﹣x+2．
（2）m＝1或m＝或m＝2．
（3）P（），Q（0， ）或P（），Q（0.）或P（），Q（0，1）或P（1+），Q（0，﹣2）．
【解答】解：（1）∵抛物线y＝ax2+bx+c过点A（﹣1，0），B（2，0），
∴抛物线的表达式为y＝a（x+1）（x﹣2），
将点C（0，2）代入得，2＝﹣2a，
∴a＝﹣1，
∴抛物线的表达式为y＝﹣（x+1）（x﹣2），即y＝﹣x2+x+2．
设直线BC的表达式为y＝kx+t，
将B（2，0），C（0，2）代入得，
，
解得，
∴直线BC的表达式为y＝﹣x+2．
（2）∵点M在直线BC上，且P（m，n），
∴点M的坐标为（m，﹣m+2），
∴OC＝2
∴CM2＝（m﹣0）2+（﹣m+2﹣2）2＝2m2，OM2＝m2+（﹣m+2）2＝2m2﹣4m+4，
当△OCM为等腰三角形时，
①若CM＝OM，则CM2＝OM2，
即2m2＝2m2﹣4m+4，
解得m＝1；
②若CM＝OC，则CM2＝OC2，
即2m2＝4，
解得或m＝﹣（舍去）；
③若OM＝OC，则OM2＝OC2，
即2m2﹣4m+4＝4，
解得m＝2或m＝0（舍去）．
综上，m＝1或m＝或m＝2．
（3）∵点P与点C相对应，
∴△POQ∽△CBN或△POQ∽△CNB，
①若点P在点B的左侧，
则，
当△POQ∽△CBN，即∠POQ＝45°时，
直线OP的表达式为y＝x，
∴﹣m2+m+2＝m，
解得或m＝﹣（舍去），
∴，即OP＝2，
∴，即，
解得OQ＝，
∴，
当△POQ∽△CNB，即∠PQO＝45°时，
，
∴，即，
解得m＝1±（舍去）．
当△POQ∽△CNB，即∠PQO＝45°时，
PQ＝，OQ＝m﹣（﹣m2+m+2）＝m2﹣2，
∴，即，
解得m＝，（负值舍去），
∴P（），Q（0.）．
②若点P在点B的右侧，
则∠CBN＝135°，BN＝m﹣2，
当△POQ∽△CBN，即∠POQ＝135°时，
直线OP的表达式为y＝﹣x，
∴﹣m2+m+2＝﹣m，
解得m＝1+或m＝1﹣（舍去），
∴，
∴，即，
解得OQ＝1，
∴，
当△POQ∽△CNB，即∠PQO＝135°时，
PQ＝，OQ＝|﹣m2+m+2+m|＝m2﹣2m﹣2，
∴，即，
解得m＝1+或m＝1﹣（舍去），
∴，
综上，P（），Q（0， ）或P（），Q（0.）或P（），Q（0，1）或P（1+），Q（0，﹣2）．
3．（2021•随州）在平面直角坐标系中，抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0）和点B，与y轴交于点C，顶点D的坐标为（1，﹣4）．
（1）直接写出抛物线的解析式；
（2）如图1，若点P在抛物线上且满足∠PCB＝∠CBD，求点P的坐标；
（3）如图2，M是直线BC上一个动点，过点M作MN⊥x轴交抛物线于点N，Q是直线AC上一个动点，当△QMN为等腰直角三角形时，直接写出此时点M及其对应点Q的坐标．

【答案】（1）y＝x2﹣2x﹣3；
（2）P1（4，5），P2（，﹣）；
（3）M1（，），Q1（﹣，）；M2（，﹣），Q2（﹣，﹣）；M3（5，2），Q3（﹣5，12）；M4（2，﹣1），Q4（0，﹣3）；M5（7，4），Q5（﹣7，18）；M6（1，﹣2），Q6（0，﹣3）．
【解答】解：（1）∵顶点D的坐标为（1，﹣4），
∴设抛物线的解析式为y＝a（x﹣1）2﹣4，将点A（﹣1，0）代入，
得0＝a（﹣1﹣1）2﹣4，
解得：a＝1，
∴y＝（x﹣1）2﹣4＝x2﹣2x﹣3，
∴该抛物线的解析式为y＝x2﹣2x﹣3；
（2）∵抛物线对称轴为直线x＝1，A（﹣1，0），
∴B（3，0），
设直线BD解析式为y＝kx+e，
∵B（3，0），D（1，﹣4），
∴，
解得：，
∴直线BD解析式为y＝2x﹣6，
①当点P在直线BC的上方时，如图1，过点C作CP1∥BD，交抛物线于点P1，
设直线CP1的解析式为y＝2x+d，将C（0，﹣3）代入，
得﹣3＝2×0+d，
解得：d＝﹣3，
∴直线CP1的解析式为y＝2x﹣3，
结合抛物线y＝x2﹣2x﹣3，可得x2﹣2x﹣3＝2x﹣3，
解得：x1＝0（舍），x2＝4，
故P1（4，5）；
②当点P在直线BC的下方时，
方法一：如图1，过点B作y轴平行线，过点C作x轴平行线交于点G，
∵OB＝OC，∠BOC＝∠OBG＝∠OCG＝90°，
∴四边形OBGC是正方形，
设CP1与x轴交于点E，则2x﹣3＝0，
解得：x＝，
∴E（，0），
在x轴下方作∠BCF＝∠BCE交BG于点F，
∵四边形OBGC是正方形，
∴OC＝CG＝BG＝3，∠COE＝∠G＝90°，∠OCB＝∠GCB＝45°，
∴∠OCB﹣∠BCE＝∠GCB﹣∠BCF，
即∠OCE＝∠GCF，
∴△OCE≌△GCF（ASA），
∴FG＝OE＝，
∴BF＝BG﹣FG＝3﹣＝，
∴F（3，﹣），
设直线CF解析式为y＝k1x+e1，
∵C（0，﹣3），F（3，﹣），
∴，
解得：，
∴直线CF解析式为y＝x﹣3，
结合抛物线y＝x2﹣2x﹣3，可得x2﹣2x﹣3＝x﹣3，
解得：x1＝0（舍），x2＝，
∴P2（，﹣），
方法二：如图1′，连接CD，取BD的中点F，连接CF并延长交抛物线于点P，过点D作DT⊥y轴于点T，
∵B（3，0），C（0，﹣3），D（1，﹣4），
∴OB＝OC＝3，CT＝DT＝1，
∵∠BOC＝∠CTD＝90°，
∴△BOC和△CDT均为等腰直角三角形，
∴∠BCO＝∠DCT＝45°，
∴∠BCD＝180°﹣45°﹣45°＝90°，
∵点F是BC的中点，
∴CF＝BF＝DF，
∴∠PCB＝∠CBD，
∵F（，），即F（2，﹣2），
设直线CF的解析式为y＝k2x+e2，则，
解得：，
∴直线CF的解析式为y＝x﹣3，
由x2﹣2x﹣3＝x﹣3，解得：x＝0（舍去）或x＝，
∴P（，﹣）；
综上所述，符合条件的P点坐标为：P1（4，5），P2（，﹣）；
（3）设直线AC解析式为y＝m1x+n1，直线BC解析式为y＝m2x+n2，
∵A（﹣1，0），C（0，﹣3），
∴，
解得：，
∴直线AC解析式为y＝﹣3x﹣3，
∵B（3，0），C（0，﹣3），
∴，
解得：，
∴直线BC解析式为y＝x﹣3，
设M（t，t﹣3），则N（t，t2﹣2t﹣3），
∴MN＝|t2﹣2t﹣3﹣（t﹣3）|＝|t2﹣3t|，
①当△QMN是以NQ为斜边的等腰直角三角形时，此时∠NMQ＝90°，MN＝MQ，如图2，
∵MQ∥x轴，
∴Q（﹣t，t﹣3），
∴|t2﹣3t|＝|t﹣（﹣t）|，
∴t2﹣3t＝±t，
解得：t＝0（舍）或t＝或t＝，
∴M1（，﹣），Q1（﹣，﹣）；M2（，），Q2（﹣，）；
②当△QMN是以MQ为斜边的等腰直角三角形时，此时∠MNQ＝90°，MN＝NQ，如图3，
∵NQ∥x轴，
∴Q（，t2﹣2t﹣3），
∴NQ＝|t﹣|＝|t2+t|，
∴|t2﹣3t|＝|t2+t|，
解得：t＝0（舍）或t＝5或t＝2，
∴M3（5，2），Q3（﹣5，12）；M4（2，﹣1），Q4（0，﹣3）；
③当△QMN是以MN为斜边的等腰直角三角形时，
此时∠MQN＝90°，MQ＝NQ，如图4，
过点Q作QH⊥MN于H，则MH＝HN，
∴H（t，），
∴Q（，），
∴QH＝|t﹣|＝|t2+5t|，
∵MQ＝NQ，
∴MN＝2QH，
∴|t2﹣3t|＝2×|t2+5t|，
解得：t＝7或1，
∴M5（7，4），Q5（﹣7，18）；M6（1，﹣2），Q6（0，﹣3）；
综上所述，点M及其对应点Q的坐标为：
M1（，），Q1（﹣，）；M2（，﹣），Q2（﹣，﹣）；M3（5，2），Q3（﹣5，12）；M4（2，﹣1），Q4（0，﹣3）；M5（7，4），Q5（﹣7，18）；M6（1，﹣2），Q6（0，﹣3）．





4．（2022•随州）如图1，平面直角坐标系xOy中，抛物线y＝ax2+bx+c（a＜0）与x轴分别交于点A和点B（1，0），与y轴交于点C，对称轴为直线x＝﹣1，且OA＝OC，P为抛物线上一动点．
（1）直接写出抛物线的解析式；
（2）如图2，连接AC，当点P在直线AC上方时，求四边形PABC面积的最大值，并求出此时P点的坐标；
（3）设M为抛物线对称轴上一动点，当P，M运动时，在坐标轴上是否存在点N，使四边形PMCN为矩形？若存在，直接写出点P及其对应点N的坐标；若不存在，请说明理由．


【答案】（1）y＝﹣x2﹣2x+3；
（2）最大值为，此时P（﹣，）；
（3）点P（﹣1，4），N（0，4）或P（，），N（，0）或P′（，），N′（，0）．
【解答】解：（1）∵抛物线的对称轴是直线x＝﹣1，抛物线交x轴于点A，B（1，0），
∴A（﹣3，0），
∴OA＝OC＝3，
∴C（0，3），
∴可以假设抛物线的解析式为y＝a（x+3）（x﹣1），
把（0，3）代入抛物线的解析式，得a＝﹣1，
∴抛物线的解析式为y＝﹣x2﹣2x+3；

（2）如图（2）中，连接OP．设P（m，﹣m2﹣2m+3），

S＝S△PAO+S△POC+S△OBC，
＝×3×（﹣m2﹣2m+3）+×3×（﹣m）+×1×3
＝（﹣m2﹣3m+4）
＝﹣（m+）2+，
∵﹣＜0，
∴当m＝﹣时，S的值最大，最大值为，此时P（﹣，）；

（3）存在，理由如下：
如图3﹣1中，当点N在y轴上时，四边形PMCN是矩形，此时P（﹣1，4），N（0，4）；

如图3﹣2中，当四边形PMCN是矩形时，设M（﹣1，n），P（t，﹣t2﹣2t+3），则N（t+1，0），

由题意，，
消去n得，3t2+5t﹣10＝0，
解得t＝，
∴P（，），N（，0）或P′（，），N′（，0）．
综上所述，满足条件的点P（﹣1，4），N（0，4）或P（，），N（，0）或P′（，），N′（，0）．
三．矩形的性质（共1小题）
5．（2023•随州）如图，矩形ABCD的对角线AC，BD相交于点O，DE∥AC，CE∥BD．
（1）求证：四边形OCED是菱形；
（2）若BC＝3，DC＝2，求四边形OCED的面积．

【答案】（1）证明见解答；
（2）3．
【解答】（1）证明：∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形，
∵矩形ABCD的对角线AC，BD相交于点O，
∴AC＝BD，OC＝AC，OD＝BD，
∴OC＝OD，
∴四边形OCED是菱形；
（2）解：∵四边形ABCD是矩形，BC＝3，DC＝2，
∴OA＝OB＝OC＝OD，S矩形ABCD＝3×2＝6，
∴S△OCD＝S矩形ABCD＝×6＝1.5，
∵四边形OCED是菱形，
∴菱形OCED的面积＝2S△OCD＝2×1.5＝3．
四．四边形综合题（共1小题）
6．（2022•随州）《几何原本》是古希腊数学家欧几里得的一部不朽著作，是数学发展史的一个里程碑．在该书的第2卷“几何与代数”部分，记载了很多利用几何图形来论证的代数结论，利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中．
（1）我们在学习许多代数公式时，可以用几何图形来推理，观察下列图形，找出可以推出的代数公式，（下面各图形均满足推导各公式的条件，只需填写对应公式的序号）

公式①：（a+b+c）d＝ad+bd+cd
公式②：（a+b）（c+d）＝ac+ad+bc+bd
公式③：（a﹣b）2＝a2﹣2ab+b2
公式④：（a+b）2＝a2+2ab+b2
图1对应公式 　①　，图2对应公式 　②　，图3对应公式 　④　，图4对应公式 　③　．
（2）《几何原本》中记载了一种利用几何图形证明平方差公式（a+b）（a﹣b）＝a2﹣b2的方法，如图5，请写出证明过程；（已知图中各四边形均为矩形）
（3）如图6，在等腰直角三角形ABC中，∠BAC＝90°，D为BC的中点，E为边AC上任意一点（不与端点重合），过点E作EG⊥BC于点G，作EH⊥AD于点H，过点B作BF∥AC交EG的延长线于点F．记△BFG与△CEG的面积之和为S1，△ABD与△AEH的面积之和为S2．
①若E为边AC的中点，则的值为 　2　；
②若E不为边AC的中点时，试问①中的结论是否仍成立？若成立，写出证明过程；若不成立，请说明理由．

【答案】（1）①，②，④，③；
（2）证明见解答观察；
（3）①2；
②E不为边AC的中点时①中的结论仍成立，证明见解答过程．
【解答】（1）解：观察图象可得：
图1对应公式①，图2对应公式②，图3对应公式④，图4对应公式③；
故答案为：①，②，④，③；
（2）证明：
如图：

由图可知，矩形BCEF和矩形EGHL都是正方形，
∵AK＝BM＝BF﹣MF＝a﹣b，BD＝BC﹣CD＝a﹣b，
∴S矩形AKLC＝AK•AC＝a（a﹣b）＝BF•BD＝S矩形DBFG，
∴S正方形BCEF＝a2＝S矩形CDHL+S矩形DBFG+S正方形EGHL＝S矩形CDHL+S矩形AKLC+b2，
∴a2＝S矩形AKHD+b2，
∵S矩形AKHD＝AK•AD＝（a﹣b）（a+b），
∴a2＝（a﹣b）（a+b）+b2，
∴（a+b）（a﹣b）＝a2﹣b2；
（3）解：①设BD＝m，
由已知可得△ABD、△AEH、△CEG、△BFG是等腰直角三角形，四边形DGEH是矩形，
∴AD＝BD＝CD＝m，
∵E是AC中点，
∴HE＝DG＝m＝AH，
∴CG＝CD﹣DG＝m，BG＝FG＝BD+DG＝m，
∴S1＝S△BFG+S△CEG＝×m×m+×m×m＝m2，
S2＝S△ABD+S△AEH＝m2+×m×m＝m2，
∴＝2；
故答案为：2；
②E不为边AC的中点时①中的结论仍成立，证明如下：
设BD＝a，DG＝b，
由已知可得△ABD、△AEH、△CEG、△BFG是等腰直角三角形，四边形DGEH是矩形，
∴AD＝BD＝CD＝a，AH＝HE＝DG＝b，EG＝CG＝a﹣b，FG＝BG＝a+b，
∴S1＝S△BFG+S△CEG＝×（a+b）2+×（a﹣b）2＝a2+b2，
S2＝S△ABD+S△AEH＝a2+×b2＝（a2+b2），
∴＝2．
五．切线的性质（共2小题）
7．（2022•随州）如图，已知D为⊙O上一点，点C在直径BA的延长线上，BE与⊙O相切，交CD的延长线于点E，且BE＝DE．
（1）判断CD与⊙O的位置关系，并说明理由；
（2）若AC＝4，sinC＝，
①求⊙O的半径；
②求BD的长．

【答案】（1）证明见解析部分；
（2）①2；
②．
【解答】解：（1）结论：CD是⊙O的切线；
理由：如图，连接OD．
∵EB＝ED，OB＝OD，
∴∠EBD＝∠EDB，∠OBD＝∠ODB，
∵BE是⊙O的切线，OB是半径，
∴OB⊥BE，
∴∠OBE＝90°，
∴∠EBD+∠OBD＝90°，
∴∠EDB+∠ODB＝90°，
∴OD⊥DE，
∵OD是半径，
∴CD是⊙O的切线；

（2）①设OD＝OA＝r，
∵OD⊥CD，
∴sinC＝＝，
∴＝，
∴r＝2，
∴⊙O的半径为2；

②在Rt△COD中，CD＝＝＝4，
∵AB是直径，
∴∠ADB＝90°，
∴∠DBA+∠BAD＝90°，
∵OD＝OA，
∴∠OAD＝∠ODA，
∵∠ADC+∠ODA＝90°，
∴∠ADC＝∠CBD，
∵∠C＝∠C，
∴△CDA∽△CBD，
∴＝＝＝，
设AD＝k，BD＝2k，
∵AD2+BD2＝AB2，
∴（k）2+（2k）2＝42，
∴k＝（负根已经舍去），
∴BD＝2k＝．

8．（2021•随州）如图，D是以AB为直径的⊙O上一点，过点D的切线DE交AB的延长线于点E，过点B作BC⊥DE交AD的延长线于点C，垂足为点F．
（1）求证：AB＝BC；
（2）若⊙O的直径AB为9，sinA＝．
①求线段BF的长；
②求线段BE的长．

【答案】（1）证明见解析；
（2）①1；②．
【解答】解：（1）证明：连接OD，如图1，

∵DE是⊙O的切线，
∴OD⊥DE．
∵BC⊥DE，
∴OD∥BC．
∴∠ODA＝∠C．
∵OA＝OD，
∴∠ODA＝∠A．
∴∠A＝∠C．
∴AB＝BC．
（2）①连接BD，则∠ADB＝90°，如图2，

在Rt△ABD中，
∵sinA＝，AB＝9，
∴BD＝3．
∵OB＝OD，
∴∠ODB＝∠OBD．
∵∠OBD+∠A＝∠FDB+∠ODB＝90°，
∴∠A＝∠FDB．
∴sin∠A＝sin∠FDB．
在Rt△BDF中，
∵sin∠BDF＝＝，
∴BF＝1．
②由（1）知：OD∥BF，
∴△EBF∽△EOD．
∴．
即：．
解得：BE＝．
六．切线的判定与性质（共1小题）
9．（2023•随州）如图，AB是⊙O的直径，点E，C在⊙O上，点C是的中点，AE垂直于过C点的直线DC，垂足为D，AB的延长线交直线DC于点F．
（1）求证：DC是⊙O的切线；
（2）若AE＝2，sin∠AFD＝，
①求⊙O的半径；
②求线段DE的长．

【答案】（1）证明过程见解答；
（2）①⊙O的半径为3；
②线段DE的长为2．
【解答】（1）证明：连接OC，

∵AD⊥DF，
∴∠D＝90°，
∵点C是的中点，
∴＝，
∴∠DAC＝∠CAB，
∴OA＝OC，
∴∠CAB＝∠OCA，
∴∠DAC＝∠OCA，
∴AD∥OC，
∴∠OCF＝∠D＝90°，
∵OC是⊙O的半径，
∴DC是⊙O的切线；
（2）解：①过点O作OG⊥AE，垂足为G，

∴AG＝EG＝AE＝1，
∵OG⊥AD，
∴∠AGO＝∠DGO＝90°，
∵∠D＝∠AGO＝90°，
∴OG∥DF，
∴∠AFD＝∠AOG，
∵sin∠AFD＝，
∴sin∠AOG＝sin∠AFD＝，
在Rt△AGO中，AO＝＝＝3，
∴⊙O的半径为3；
②∵∠OCF＝90°，
∴∠OCD＝180°﹣∠OCF＝90°，
∵∠OGE＝∠D＝90°，
∴四边形OGDC是矩形，
∴OC＝DG＝3，
∵GE＝1，
∴DE＝DG﹣GE＝3﹣1＝2，
∴线段DE的长为2．
七．圆的综合题（共1小题）
10．（2021•随州）等面积法是一种常用的、重要的数学解题方法．它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题，在解题中，灵活运用等面积法解决相关问题，可以使解题思路清晰，解题过程简便快捷．
（1）在直角三角形中，两直角边长分别为3和4，则该直角三角形斜边上的高的长为 　　，其内切圆的半径长为 　1　；
（2）①如图1，P是边长为a的正△ABC内任意一点，点O为△ABC的中心，设点P到△ABC各边距离分别为h1，h2，h3，连接AP，BP，CP，由等面积法，易知a（h1+h2+h3）＝S△ABC＝3S△OAB，可得h1+h2+h3＝　　；（结果用含a的式子表示）

②如图2，P是边长为a的正五边形ABCDE内任意一点，设点P到五边形ABCDE各边距离分别为h1，h2，h3，h4，h5，参照①的探索过程，试用含a的式子表示h1+h2+h3+h4+h5的值．（参考数据：tan36°≈，tan54°≈）
（3）①如图3，已知⊙O的半径为2，点A为⊙O外一点，OA＝4，AB切⊙O于点B，弦BC∥OA，连接AC，则图中阴影部分的面积为 　　；（结果保留π）
②如图4，现有六边形花坛ABCDEF，由于修路等原因需将花坛进行改造，若要将花坛形状改造成五边形ABCDG，其中点G在AF的延长线上，且要保证改造前后花坛的面积不变，试确定点G的位置，并说明理由
【答案】（1），1；
（2）①，②；
（3）①，②见解析．
【解答】解：（1）如图所示，AC＝3，BC＝4，∠ACB＝90°，
∴AB＝＝5，设斜边上高为h，由等面积法可知：
AC•BC＝h•AB，
＝．
设其内切圆半径为r，利用分割图形后各部分的面积之和等于原图形的面积可得：
S△ABC＝S△ACO+S△BCO+S△ABO．
即3×4÷2＝AC•r+BC•r+AB•r，
即＝6，
∴r＝＝＝1．
故答案为：，1；
（2）①：由已知中图可知，△ABC的面积为＝，
由等面积法，易知a（h1+h2+h3）＝S△ABC＝，
解得：h1+h2+h3＝．
故答案为：．
②：类比①中方法可知（h1+h2+h3+h4+h5）＝S五边形ABCDE，
设点O为正五边形ABCDE的中心，连接OA，OB，如图2．
易知S五边形ABCDE＝5S△OAB，
过O作OQ⊥AB于点Q，∠EAB＝＝108°，
故∠OAQ＝54°，OQ＝AQ•tan54°＝，
故（h1+h2+h3+h4+h5）＝5××，从而得到：
h1+h2+h3+h4+h5＝tan54°≈．
（3）①：若以BC作为△OCB和△ACB的底，则△OCB和△ACB等高，
∴S△OCB＝S△ACB．
∴图中阴影部分的面积即为扇形OCB的面积．
∵AB切⊙O于点B，
∴∠OBA＝90°，
又OB＝2，OA＝4，
∴∠OAB＝30°，∠AOB＝60°，
∵BC∥OA，
∴∠OBC＝∠AOB＝60°，
∴△OCB为等边三角形．
∴∠COB＝60°，
∴S扇形OCB＝＝．
故阴影部分面积为．
故答案为：．
②如图3，连接DF，过点E作EG∥DF交AF的延长线于点G，则点G即为所求．
连接DG，
∵S六边形ABCDEF＝S五边形ABCDF+S△DEF，
∵EG∥DF，
∴S△DEF＝S△DGF，
∴S六边形ABCDEF＝S五边形ABCDF+S△DGF＝S五边形ABCDG．



八．几何变换综合题（共1小题）
11．（2023•随州）1643年，法国数学家费马曾提出一个著名的几何问题：给定不在同一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最小的点的位置，意大利数学家和物理学家托里拆利给出了分析和证明，该点也被称为“费马点”或“托里拆利点”，该问题也被称为“将军巡营”问题．
（1）下面是该问题的一种常见的解决方法，请补充以下推理过程：（其中①处从“直角”和“等边”中选择填空，②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空，③处填写角度数，④处填写该三角形的某个顶点）
当△ABC的三个内角均小于120°时，
如图1，将△APC绕点C顺时针旋转60°得到△A′P′C，连接PP′，
由PC＝P′C，∠PCP′＝60°，可知△PCP′为 　等边　三角形，故PP′＝PC，又P′A′＝PA，故PA+PB+PC＝P′A′+PB+PP′≥A′B，
由 　两点之间线段最短　可知，当B，P，P′，A′在同一条直线上时，PA+PB+PC取最小值，如图2，最小值为A′B，此时的P点为该三角形的“费马点”，
且有∠APC＝∠BPC＝∠APB＝　120°　；
已知当△ABC有一个内角大于或等于120°时，“费马点”为该三角形的某个顶点．如图3，若∠BAC≥120°，则该三角形的“费马点”为 　A　点．
（2）如图4，在△ABC中，三个内角均小于120°，且AC＝3，BC＝4，∠ACB＝30°，已知点P为△ABC的“费马点”，求PA+PB+PC的值；

（3）如图5，设村庄A，B，C的连线构成一个三角形，且已知AC＝4km，BC＝2km，∠ACB＝60°．现欲建一中转站P沿直线向A，B，C三个村庄铺设电缆，已知由中转站P到村庄A，B，C的铺设成本分别为a元/km，a元/km，a元/km，选取合适的P的位置，可以使总的铺设成本最低为 　　元．（结果用含a的式子表示）
【答案】（1）等边；两点之间线段最短；120°；A；
（2）5；
（3）a．
【解答】解：（1）∵PC＝P'C，∠PCP'＝60°，
∴△PCP'为等边三角形，
∴PP'＝PC，∠P'PC＝∠PP'C＝60°，
又∵P'A'＝PA，
∴PA+PB+PC＝PA'+PB+PP'≥A'B，
根据两点之间线段最短可知，当B、P、P'、A在同一条直线上时，PA+PB+PC取最小值，最小值为A'B，
此时的P点为该三角形的“费马点”，
∴∠BPC+∠P'PC＝180°，∠A'P'C+∠PP'C＝180°，
∴∠BPC＝120°，∠A'P'C＝120°，
∵将△APC绕点C顺时针旋转60°得到△A′P′C，
∴△APC≌△A'P'C，
∴∠APC＝∠AP'C'＝120°，
∴∠APB＝360°﹣120°﹣120°＝120°，
∴∠APC＝∠BPC＝∠APB＝120°，
∵∠BAC≥120°，
∴BC＞AC，BC＞AB，
∴BC+AB＞AC+AB，BC+AC＞AB+AC，
∴三个顶点中顶点A到另外两个顶点的距离和最小，
又∵已知当△ABC有一个内角大于或等于120°时，“费马点”为该三角形的某个顶点，
∴该三角形的“费马点”为点A．
故答案为：等边；两点之间线段最短；120°；A；
（2）如图4，将△APC绕点C顺时针旋转60°得到△A'P'C，连接PP'，

由（1）可知当B、P、P'、A在同一条直线上时，PA+PB+PC取最小值，最小值为A'B，
∵∠ACP＝∠A'CP'，
∴∠ACP+∠BCP＝∠A'CP'+∠BCP＝∠ACB＝30°，
又∵∠PCP'＝60°，
∴∠BCA'＝90°，
根据旋转的性质可知：AC＝A'C＝3，
∴A'B＝，
即PA+PB+PC的最小值为5；
（3）∵总铺设成本＝PA×a+PB×a+PC×a＝，
∴当PA+PB+PC最小时，总铺设成本最低，
将△APC绕点C顺时针旋转90°得到△A'P'C，连接PP'，A'B，

由旋转性质可知：P'C＝PC，∠PCP'＝∠ACA'＝90°，P'A'＝PA，A'C＝AC＝4km，
∴PP'＝PC，
∴PA+PB+PC＝P'A'+PB+PP'，
当B、P、P'、A在同一条直线上时，P'A'+PB+PP'取最小值，
即PA+PB+PC取最小值为A'B，
过点A'作A'H⊥BC于H，
∵∠ACB＝60°，∠ACA'＝90°，
∴∠A'CH＝30°，
∴A'H＝A'C＝2km，
∴HC＝＝（km），
∴BH＝BC+CH＝（km），
∴A'B＝（km），
即PA+PB+PC的最小值为km，
总铺设成本为：总铺设成本＝＝a（元）．
故答案为：a．
九．解直角三角形的应用-仰角俯角问题（共1小题）
12．（2023•随州）某校学生开展综合实践活动，测量某建筑物的高度AB，在建筑物附近有一斜坡，坡长CD＝10米，坡角α＝30°，小华在C处测得建筑物顶端A的仰角为60°，在D处测得建筑物顶端A的仰角为30°．（已知点A，B，C，D在同一平面内，B，C在同一水平线上）
（1）求点D到地面BC的距离；
（2）求该建筑物的高度AB．

【答案】（1）点D到地面BC的距离为5m．
（2）居民楼的高度AB为15m．
【解答】解：（1）过点D作DE⊥BC，交BC的延长线于点E，
∵cosα＝，
解得CE＝5，
∴DE＝＝5（m）．
∴点D到地面BC的距离为5m．
（2）过点D作DF⊥AB于点F，
则BF＝DE＝5m，
设BC＝xm，则BE＝DF＝（5+x）m，
在Rt△ABC中，tan60°＝，
解得AB＝x，
∴AF＝（x﹣5）m，
在Rt△ADF中，tan30°＝＝＝，
解得x＝5，
经检验，x＝5是原方程的解且符合题意，
∴AB＝＝15（m）．
∴居民楼的高度AB为15m．

一十．列表法与树状图法（共1小题）
13．（2021•随州）疫苗接种初期，为更好地响应国家对符合条件的人群接种新冠疫苗的号召，某市教育部门随机抽取了该市部分七、八、九年级教师，了解教师的疫苗接种情况，得到如下统计表：

已接种
未接种
合计
七年级
30
10
40
八年级
35
15
a
九年级
40
b
60
合计
105
c
150
（1）表中，a＝　50　，b＝　20　，c＝　45　；
（2）由表中数据可知，统计的教师中接种率最高的是 　七　年级教师；（填“七”或“八”或“九”）
（3）若该市初中七、八、九年级一共约有8000名教师，根据抽样结果估计未接种的教师约有 　2400　人；
（4）为更好地响应号召，立德中学从最初接种的4名教师（其中七年级1名，八年级1名，九年级2名）中随机选取2名教师谈谈接种的感受，请用列表或画树状图的方法，求选中的两名教师恰好不在同一年级的概率．
【答案】（1）50，20，45；
（2）七；
（3）2400；
（4）．
【解答】解：（1）a＝35+15＝50，b＝60﹣40＝20，c＝10+15+20＝45，
故答案为：50，20，45；
（2）七年级教师的接种率为：30÷40×100%＝75%，八年级教师的接种率为：35÷50×100%＝70%，九年级教师的接种率为：40÷60×100%≈67%，
∵75%＞70%＞67%，
∴统计的教师中接种率最高的是七年级教师，
故答案为：七；
（3）根据抽样结果估计未接种的教师约有：8000×＝2400（人），
故答案为：2400；
（4）把七年级1名教师记为A，八年级1名教师记为B，九年级2名教师记为C、D，
画树状图如图：

共有12种等可能的结果，选中的两名教师恰好不在同一年级的结果有10种，
∴选中的两名教师恰好不在同一年级的概率为＝．